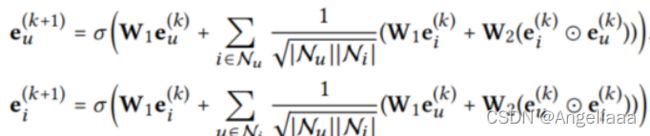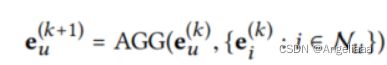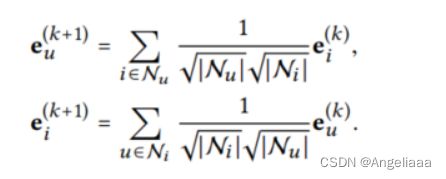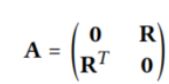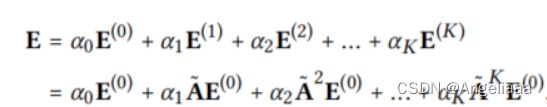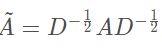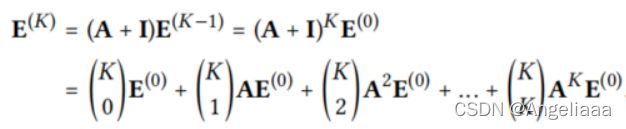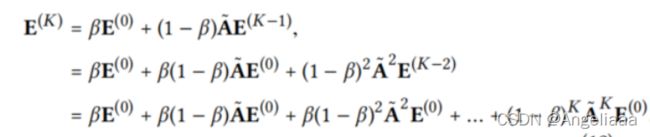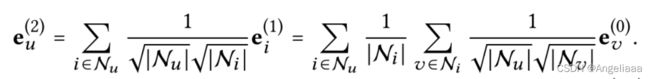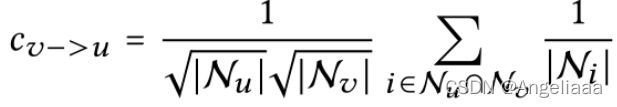LightGCN

1.简介

本文提出了一种轻型但是有效的GCN网络用于推荐系统，它舍弃了传统GCN的特征变换和非线性激活，并通过实验验证了这两种操作对协同过滤是无效的，同时提出了一种轻量级的GCN网络构建模型（LightGCN）用于推荐系统。

LightGCN它只包含GCN中最基本的结构（邻居聚合）用于协同过滤。LightGCN通过在用户-物品交互矩阵上进行线性传播来学习用户和物品的嵌入，最后将所有层学习到的嵌入的加权和作为最终嵌入。这种简单、线性的模型是很容易实施和训练的，并且在同样的实验条件下相对于NGCF（一种最好的基于GCN的推荐模型）有了实质性的改善（相对平均提升了16.0%）

总之，主要的贡献如下：

1.实验结果表明，GCN中两种常见的设计，即特征转换和非线性激活，对协同过滤的效果没有积极影响

2.我们提出了LightGCN，它只包含GCN中最基本的组件以供推荐，从而大大简化了模型设计。

3.我们通过遵循相同的设置对LightGCN和NGCF进行了经验比较，并证明了改进。在从技术和经验两个角度对LightGCN的合理性进行了深入分析。

2.准备工作

我们首先介绍了NGCF，并证明了NGCF中两种操作（特征变换和非线性激活）对协同过滤来说没有用。

2.1NGCF概述：

       在半监督的节点分类中，每个节点都含有丰富的语义特征进行输入，多层的特征变换和非线性变换对于特征学习来说是有益的。但是在协同过滤任务中，每个在交互矩阵中的节点只有一个ID输入，且这个ID是没有如何语义的（不包含特征信息），所以特征变换和非线性激活不会使网络学习到更多特征，更糟糕的是，它还会增加训练难度。

2.2NGCF的实证研究

 对NGCF做了简化

1.NGCF-f，移除了特征变换矩阵W1和W2

2.NGCF-n，移除了非线性激活函数

3.NGCF-nf，同时移除了非线性激活函数和特征变换矩阵

 测试得到如下效果： 

我们可以得到以下结论：

1.添加特征变换对NGCF产生了负面影响，因为对NGCF和NGCF-n两种模型中消除了特征变换后，都显著提高了NGCF的性能；

2.当特征变化在时加入非线性激活对模型的影响较小，但当特征变换被禁用时，加入非线性激活会产生负面影响。

3.总体而言，特征变换和非线性激活对NGCF产生了相当负面的影响，因为同时去除它们，NGCF-fn比NGCF有很大的提高（召回率相对提高9.57%）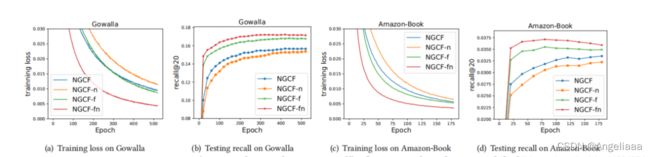

 3.LightGCN模型

      LightGCN模型可以分为轻型图卷积和层聚合两部分，如下图：

       GCN的基本思想是通过在图上平滑特征从而学习节点表示。为了达到此目的，迭代的从邻居聚合特征作为新的节点表示。节点聚合可以表示为：

3.1Light Graph Convolution

       在LightGCN中，采用简单的加权求和方法，并且舍弃了特征变换和非线性激活。卷积操作可以表示为：

       在LightGCN中，我们的聚合只使用了邻居节点而没有整合节点自己(self-connections)。

3.2层组合（layer combination）与模型预测

      在LightGCN中，训练用的模型参数只有第0层。参数经过k层后，会得到最终表示：

      其中 ≥ 0表示第k层嵌入在构成最终嵌入中的重要性。

      使用层聚合的原因：

       随着层数的增加，嵌入会变得过于光滑。因此，仅使用最后一层是有问题的。

       不同层的嵌入具有不同的语义。

       将不同层的嵌入与加权和结合起来，可以捕获带有自连接的图卷积的效果，这是GCN中的一个重要技巧

    模型预测被定义成内积：

 3.3矩阵形式：

       为了促进现有模型的实施与讨论，我们提供了LightGCN的矩阵形式，用户-物品的邻接矩阵可以看成下图：其中M和N分别表示用户和项目数，每个条目的值为1代表用户u与项目i交互。

     第0层的嵌入矩阵为： T为嵌入大小，LGC的矩阵等效形式可以表示为：

    D是（M+N）*(M+N)的对角矩阵，其中每个条目Dii表示邻接矩阵A（也称为度矩阵）的第i行向量中非零条目的数量。
    最后我们可以得到最后的嵌入矩阵用于模型预测：

    为对称归一化矩阵。

3.3.1与SGCN的关系(增加自连接self-connections)

 SGCN也移除了权重矩阵和非线性函数，可以表示为：

 I是一个单位矩阵，它给A添加了自连接(self-connections)，在随后的分析中，为了简化我们舍弃了因为它们只是重新缩放嵌入。在SGCN，最后一层的嵌入用于下游任务，表示成：

 上诉推导说明，把自连接放入A中并且传播嵌入等价于每一层的LGC加权求和。

3.3.2与APPNP的关系（防止过平滑问题）

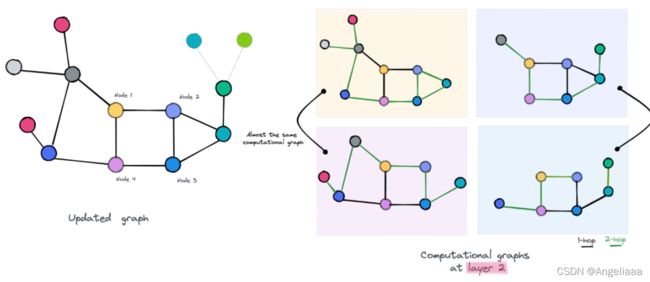
【过平滑问题】：

消息传递框架使用了前面介绍的两个主要函数 Aggregate 和 Update，它们从邻居那里收集特征向量并将它们与节点自己的特征结合起来更新它们的表示。此操作的工作方式使交互节点（在此过程中）具有非常相似的表示。

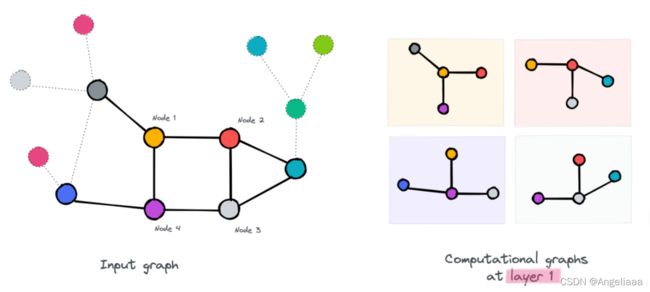
我们将尝试在我们模型的第一层中说明这一点，以说明为什么会发生平滑，然后添加更多层以显示这种表示平滑如何随层增加。

       正如您在第一层中看到的，节点可以访问单跳邻居。例如，您还可以观察到，节点 2 和节点 3 几乎可以访问相同的信息，因为它们相互链接并具有共同的邻居，唯一的区别是它们的最后一个邻居（紫色和黄色）。我们可以预测它们的嵌入会略有相似。对于节点 1 和节点 4，它们彼此交互但具有不同的邻居。所以我们可以预测他们的新嵌入会有所不同。

我们通过为每个节点分配新的嵌入来更新我们的图，然后移动到第二层并执行相同的过程  

在我们 GNN 的第二层，节点 1,4 和 2,3 的计算图分别几乎相同。因为额外的层使他们可以访问更多图的部分，增加了访问相同节点的可能性，所以原本在第一层上不相同的节点1和4，现在竟然惊人的相似！

        APPNP可以传播很多层而不会过平滑，每一层都会取得第0层的嵌入表示，就是这样利用原始特征来对每个传播层进行补充，从而可以保持局部性需要，可表示为：

       β是控制在传播中起始特征的保留率，是归一化邻接矩阵。在APPNP中，它的最后一层作为最终的预测结果：

       可以看出，等式12与等式8类似，设置相应的可以使LightGCN和APPNP相等。因此，LightGCN也有类似于APPNP相似的抗过平滑的作用。

那么LightGCN为什么会有抗平滑的作用呢?

 我们可以看到，如果另一个用户v与目标用户u进行了交互，则v 在u上的平滑度将通过系数表示：

 二阶邻居v对u的影响是由以下因素决定的,即的大小受以下因素影响：

1.协同交互项的数量越多，就越大。

2.协同交互项的受欢迎程度越低，那么就更能表示用户的个性化偏好，则uv之间的平滑度就越大。（受欢迎程度越低表示两者的特征越相似，越受欢迎的物品大家都喜欢则不能体现后买其用户的特征）

3.v的活性（就是给v不是谁都爱，什么都喜欢的话，那么v的交互项就非常有参考价值），活性越弱越大

4.实验

4.1超参数设置

设置为，k为层数，我们测试了k从1到4

 4.2对比实验

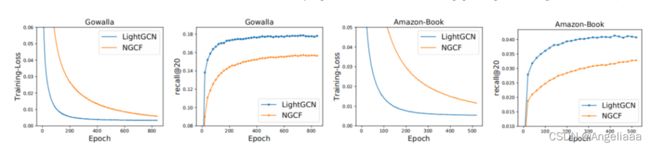
4.2.1与NGCF对比表现

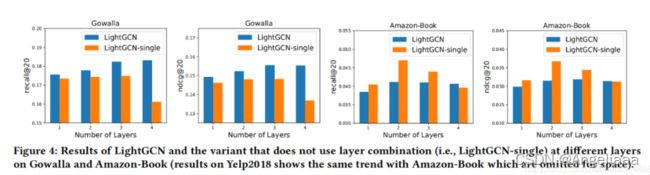
4.2.2层结合的重要性

LightGCN-single没有使用层结合，而是直接使用最后一层做预测

 4.2.3对称Sqrt归一化的影响

 5.总结和展望

1.在层组合时的重要性参数α的设定文章中没有对其进行深入的研究，可以对其进行研究，例如文中提到的针对不同的用户和物品进行个性化设置

2.知识图谱中的传播机制是否也存在于GCN类似的问题，是否可以同样去除非线性激活与特征转换等非必要的神经操作