【密码学】一文读懂ZUC算法

密码学 一文读懂ZUC密码

这次在来聊一个国产密码, 祖冲之算法（ZUC）是中华人民共和国政府采用的一种序列密码标准，由国家密码管理局于2012年3月21日发布，相关标准为“GM/T 0001-2016 祖冲之序列密码算法”，2016年10月成为中国国家密码标准（GB/T 33133-2016）。祖冲之算法于2011年9月被3GPP采纳为国际加密标准（TS 35.221），可供LTE移动终端选用。【维基百科】

算法简介

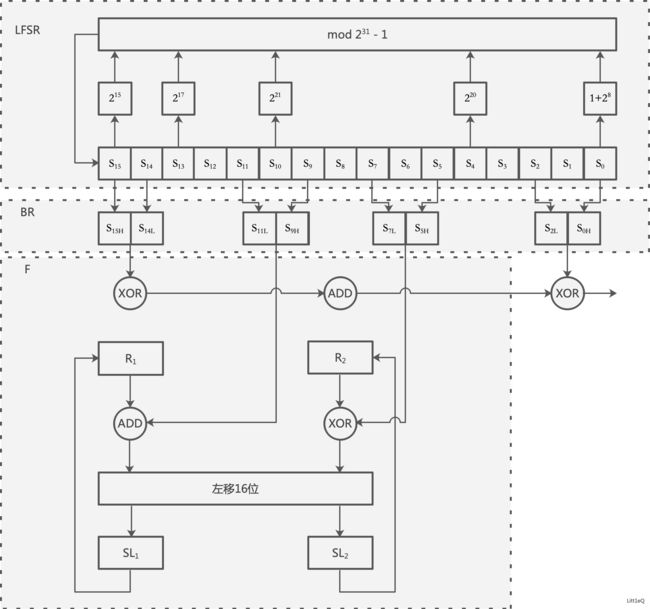
祖冲之算法结构分为三层, 第一层是线性反馈移位寄存器(LFSR), 第二层是比特重组(BR), 最后一层是非线性函数F, 下图参考参考资料当中的pdf。

线性反馈移位寄存器LFSR

初始化模式

在初始化模式下，LFSR接受一个31bit的字u, u是通过非线性函数F的32bit舍弃最低bit得到, 主要计算过程如下:

• $v=2^{15}{S}_{15}+2^{17}{S}_{13}+2^{21}{S}_{10}+2^{20}{S}_4+\left(1+2^8\right)S_0\mathrm{m}\mathrm{o}\mathrm{d}\left(2^{31}-1\right)$
• $S_{16}=\left(v+u\right)\mathrm{m}\mathrm{o}\mathrm{d}\left(2^{31}-1\right)$
• 如果$S_{16}=0$, 则令$S_{16}=2^{31}-1$
• ($S_1$, $S_2$, …, $S_{16}$) -> ($S_0$, $S_1$, …, $S_{15}$)

工作模式

在工作模式下，相比于初始化模式，没有输入，计算过程如下:

• $S_{16}=2^{15}{S}_{15}+2^{17}{S}_{13}+2^{21}{S}_{10}+2^{20}{S}_4+\left(1+2^8\right)S_0\mathrm{m}\mathrm{o}\mathrm{d}\left(2^{31}-1\right)$
• 如果$S_{16}=0$, 则令$S_{16}=2^{31}-1$
• ($S_1$, $S_2$, …, $S_{16}$) -> ($S_0$, $S_1$, …, $S_{15}$)

比特重组(BR)

输入为LFSR里面的变量, $S_0$, $S_2$, $S_5$, $S_7$, $S_9$, $S_{11}$, $S_{14}$, $S_{15}$, 输出为4个32bit的字，计算过程如下:

• $X_0=S_{15H}||S_{14L}$
• $X_1=S_{11L}||S_{9H}$
• $X_2=S_{7L}||S_{5H}$
• $X_3=S_{2L}||S_{0H}$

非线性函数F

F当中包含了两个32bit记忆单元变量$R_1$和$R_2$
输入为上次经过比特充足的前三个32比特字$X_0$, $X_1$, $X_2$, 输出为一个32bit字W, 计算过程如下:

• $W=\left(X_0\oplus R_1\right)+R_2$
• $W_1=R_1+X_1$
• $W_2=R_2\oplus X_2$
• $R_1=S(L_1(W_{1L}||W_{2H}))$
• $R_2=S(L_2(W_{2L}||W_{1H}))$

其中S为32比特的S-Box变换，具体S盒就不贴出来了，看代码或者文章后面的参考资料即可。$L_1$, $L_2$是32比特线性变化，定义如下:

• $L_1(X)=X\oplus (X<<<2)\oplus (X<<<10)\oplus (X<<<18)\oplus (X<<<24)$
• $L_2(X)=X\oplus (X<<<8)\oplus (X<<<14)\oplus (X<<<22)\oplus (X<<<30)$

密钥装入

密钥装入如下图所示，每个密钥和初始化向量iv分组都按照如下的方式进行拼接。

算法具体过程

算法初始化

首先装在密钥，然后记忆单元$R_1$, $R_2$均置0, 按照下面的过程重复32次:

• 比特重组
• W = F($X_0$, $X_1$, $X_2$)
• LFSR初始化模式

密钥生成阶段

首先执行一次

• 比特重组
• W = F($X_0$, $X_1$, $X_2$)
• LFSR工作模式

第一轮输出的W丢掉不要

然后, 按照下面的方式输出32位的字

• 比特重组
• W = F($X_0$, $X_1$, $X_2$)
• 输出密钥W
• LFSR工作模式

代码实现

use std::convert::TryInto;

const S0: [u8; 256] = [
    0x3e, 0x72, 0x5b, 0x47, 0xca, 0xe0, 0x00, 0x33, 0x04, 0xd1, 0x54, 0x98, 0x09, 0xb9, 0x6d, 0xcb,
    0x7b, 0x1b, 0xf9, 0x32, 0xaf, 0x9d, 0x6a, 0xa5, 0xb8, 0x2d, 0xfc, 0x1d, 0x08, 0x53, 0x03, 0x90,
    0x4d, 0x4e, 0x84, 0x99, 0xe4, 0xce, 0xd9, 0x91, 0xdd, 0xb6, 0x85, 0x48, 0x8b, 0x29, 0x6e, 0xac,
    0xcd, 0xc1, 0xf8, 0x1e, 0x73, 0x43, 0x69, 0xc6, 0xb5, 0xbd, 0xfd, 0x39, 0x63, 0x20, 0xd4, 0x38,
    0x76, 0x7d, 0xb2, 0xa7, 0xcf, 0xed, 0x57, 0xc5, 0xf3, 0x2c, 0xbb, 0x14, 0x21, 0x06, 0x55, 0x9b,
    0xe3, 0xef, 0x5e, 0x31, 0x4f, 0x7f, 0x5a, 0xa4, 0x0d, 0x82, 0x51, 0x49, 0x5f, 0xba, 0x58, 0x1c,
    0x4a, 0x16, 0xd5, 0x17, 0xa8, 0x92, 0x24, 0x1f, 0x8c, 0xff, 0xd8, 0xae, 0x2e, 0x01, 0xd3, 0xad,
    0x3b, 0x4b, 0xda, 0x46, 0xeb, 0xc9, 0xde, 0x9a, 0x8f, 0x87, 0xd7, 0x3a, 0x80, 0x6f, 0x2f, 0xc8,
    0xb1, 0xb4, 0x37, 0xf7, 0x0a, 0x22, 0x13, 0x28, 0x7c, 0xcc, 0x3c, 0x89, 0xc7, 0xc3, 0x96, 0x56,
    0x07, 0xbf, 0x7e, 0xf0, 0x0b, 0x2b, 0x97, 0x52, 0x35, 0x41, 0x79, 0x61, 0xa6, 0x4c, 0x10, 0xfe,
    0xbc, 0x26, 0x95, 0x88, 0x8a, 0xb0, 0xa3, 0xfb, 0xc0, 0x18, 0x94, 0xf2, 0xe1, 0xe5, 0xe9, 0x5d,
    0xd0, 0xdc, 0x11, 0x66, 0x64, 0x5c, 0xec, 0x59, 0x42, 0x75, 0x12, 0xf5, 0x74, 0x9c, 0xaa, 0x23,
    0x0e, 0x86, 0xab, 0xbe, 0x2a, 0x02, 0xe7, 0x67, 0xe6, 0x44, 0xa2, 0x6c, 0xc2, 0x93, 0x9f, 0xf1,
    0xf6, 0xfa, 0x36, 0xd2, 0x50, 0x68, 0x9e, 0x62, 0x71, 0x15, 0x3d, 0xd6, 0x40, 0xc4, 0xe2, 0x0f,
    0x8e, 0x83, 0x77, 0x6b, 0x25, 0x05, 0x3f, 0x0c, 0x30, 0xea, 0x70, 0xb7, 0xa1, 0xe8, 0xa9, 0x65,
    0x8d, 0x27, 0x1a, 0xdb, 0x81, 0xb3, 0xa0, 0xf4, 0x45, 0x7a, 0x19, 0xdf, 0xee, 0x78, 0x34, 0x60
];

const S1: [u8; 256] = [
    0x55, 0xc2, 0x63, 0x71, 0x3b, 0xc8, 0x47, 0x86, 0x9f, 0x3c, 0xda, 0x5b, 0x29, 0xaa, 0xfd, 0x77,
    0x8c, 0xc5, 0x94, 0x0c, 0xa6, 0x1a, 0x13, 0x00, 0xe3, 0xa8, 0x16, 0x72, 0x40, 0xf9, 0xf8, 0x42,
    0x44, 0x26, 0x68, 0x96, 0x81, 0xd9, 0x45, 0x3e, 0x10, 0x76, 0xc6, 0xa7, 0x8b, 0x39, 0x43, 0xe1,
    0x3a, 0xb5, 0x56, 0x2a, 0xc0, 0x6d, 0xb3, 0x05, 0x22, 0x66, 0xbf, 0xdc, 0x0b, 0xfa, 0x62, 0x48,
    0xdd, 0x20, 0x11, 0x06, 0x36, 0xc9, 0xc1, 0xcf, 0xf6, 0x27, 0x52, 0xbb, 0x69, 0xf5, 0xd4, 0x87,
    0x7f, 0x84, 0x4c, 0xd2, 0x9c, 0x57, 0xa4, 0xbc, 0x4f, 0x9a, 0xdf, 0xfe, 0xd6, 0x8d, 0x7a, 0xeb,
    0x2b, 0x53, 0xd8, 0x5c, 0xa1, 0x14, 0x17, 0xfb, 0x23, 0xd5, 0x7d, 0x30, 0x67, 0x73, 0x08, 0x09,
    0xee, 0xb7, 0x70, 0x3f, 0x61, 0xb2, 0x19, 0x8e, 0x4e, 0xe5, 0x4b, 0x93, 0x8f, 0x5d, 0xdb, 0xa9,
    0xad, 0xf1, 0xae, 0x2e, 0xcb, 0x0d, 0xfc, 0xf4, 0x2d, 0x46, 0x6e, 0x1d, 0x97, 0xe8, 0xd1, 0xe9,
    0x4d, 0x37, 0xa5, 0x75, 0x5e, 0x83, 0x9e, 0xab, 0x82, 0x9d, 0xb9, 0x1c, 0xe0, 0xcd, 0x49, 0x89,
    0x01, 0xb6, 0xbd, 0x58, 0x24, 0xa2, 0x5f, 0x38, 0x78, 0x99, 0x15, 0x90, 0x50, 0xb8, 0x95, 0xe4,
    0xd0, 0x91, 0xc7, 0xce, 0xed, 0x0f, 0xb4, 0x6f, 0xa0, 0xcc, 0xf0, 0x02, 0x4a, 0x79, 0xc3, 0xde,
    0xa3, 0xef, 0xea, 0x51, 0xe6, 0x6b, 0x18, 0xec, 0x1b, 0x2c, 0x80, 0xf7, 0x74, 0xe7, 0xff, 0x21,
    0x5a, 0x6a, 0x54, 0x1e, 0x41, 0x31, 0x92, 0x35, 0xc4, 0x33, 0x07, 0x0a, 0xba, 0x7e, 0x0e, 0x34,
    0x88, 0xb1, 0x98, 0x7c, 0xf3, 0x3d, 0x60, 0x6c, 0x7b, 0xca, 0xd3, 0x1f, 0x32, 0x65, 0x04, 0x28,
    0x64, 0xbe, 0x85, 0x9b, 0x2f, 0x59, 0x8a, 0xd7, 0xb0, 0x25, 0xac, 0xaf, 0x12, 0x03, 0xe2, 0xf2
];

const D: [u32; 16] = [
    0x44D7, 0x26BC, 0x626B, 0x135E, 0x5789, 0x35E2, 0x7135, 0x09AF,
    0x4D78, 0x2F13, 0x6BC4, 0x1AF1, 0x5E26, 0x3C4D, 0x789A, 0x47AC
];

pub struct ZUC {
    s: [u32; 16],
    r1: u32,
    r2: u32,
    x: [u32; 4],
}

fn l1(bits: u32) -> u32 {
    bits ^ bits.rotate_left(2) ^ bits.rotate_left(10) ^ bits.rotate_left(18) ^ bits.rotate_left(24)
}

fn l2(bits: u32) -> u32 {
    bits ^ bits.rotate_left(8) ^ bits.rotate_left(14) ^ bits.rotate_left(22) ^ bits.rotate_left(30)
}

fn tou32(a: u32, b: u32, c: u32, d: u32) -> u32 {
    a << 24 | b << 16 | c << 8 | d
}

fn add_m(a: u32, b: u32) -> u32 {
    let c = a.wrapping_add(b);
    (c & 0x7FFFFFFF).wrapping_add(c >> 31)
    // a.wrapping_add(b) % 2147483647
}

// 这个地方是个大坑, 用u32计算会出问题
fn mul_m(a: u32, b: u32) -> u32 {
    (((a as u64) * (b as u64)) % 2147483647u64) as u32
}

impl ZUC {
    pub fn new(key: &[u8], iv: &[u8]) -> ZUC {
        let s: Vec = key.iter().zip(iv).zip(D).map(|((&key, &iv), d)| {
            (key as u32) << 23 | d << 8 | (iv as u32)
        }).collect();
        
        let mut zuc = ZUC {
            s: s.try_into().expect(""),
            r1: 0,
            r2: 0,
            x: [0; 4],
        };

        for _ in 0..32 {
            zuc.bit_reconstruction();
            let w = zuc.f();
            zuc.lfsr_with_initialization_mode(w >> 1);
        }
        zuc.generate_32bit();

        zuc
    }

    fn bit_reconstruction(&mut self) {
        self.x[0] = ((self.s[15] & 0x7FFF8000) << 1) | (self.s[14] & 0xFFFF);
        self.x[1] = ((self.s[11] & 0xFFFF) << 16) | (self.s[9] >> 15);
        self.x[2] = ((self.s[7] & 0xFFFF) << 16) | (self.s[5] >> 15);
        self.x[3] = ((self.s[2] & 0xFFFF) << 16) | (self.s[0] >> 15);
    }

    fn f(&mut self) -> u32 {
        let w = (self.x[0] ^ self.r1).wrapping_add(self.r2);
        let w1 = self.r1.wrapping_add(self.x[1]);
        let w2 = self.r2 ^ self.x[2];
        let u = l1((w1 << 16) | (w2 >> 16));
        let v = l2((w2 << 16) | (w1 >> 16));
        self.r1 = tou32(S0[(u >> 24) as usize] as u32, S1[((u >> 16) & 0xFF) as usize] as u32, S0[((u >> 8) & 0xFF) as usize] as u32, S1[(u & 0xFF) as usize] as u32);
        self.r2 = tou32(S0[(v >> 24) as usize] as u32, S1[((v >> 16) & 0xFF) as usize] as u32, S0[((v >> 8) & 0xFF) as usize] as u32, S1[(v & 0xFF) as usize] as u32);
        w
    }

    fn lfsr_with_initialization_mode(&mut self, u: u32) {
        let v = self.s[0];

        let f = mul_m(self.s[0], 256);
        let v = add_m(f, v);

        let f = mul_m(self.s[4], 1048576);
        let v = add_m(f, v);

        let f = mul_m(self.s[10], 2097152);
        let v = add_m(f, v);

        let f = mul_m(self.s[13], 131072);
        let v = add_m(f, v);

        let f = mul_m(self.s[15], 32768);
        let v = add_m(f, v);

        let mut s16 = add_m(v, u);

        if s16 == 0 {
            s16 = 2147483647;
        }

        for i in 0..15 {
            self.s[i] = self.s[i + 1];
        }

        self.s[15] = s16;
    }

    fn lfsr_with_work_mode(&mut self) {
        let v = self.s[0];

        let f = mul_m(self.s[0], 256);
        let v = add_m(f, v);

        let f = mul_m(self.s[4], 1048576);
        let v = add_m(f, v);

        let f = mul_m(self.s[10], 2097152);
        let v = add_m(f, v);

        let f = mul_m(self.s[13], 131072);
        let v = add_m(f, v);

        let f = mul_m(self.s[15], 32768);
        let mut s16 = add_m(f, v);

        if s16 == 0 {
            s16 = 2147483647;
        }

        for i in 0..15 {
            self.s[i] = self.s[i + 1];
        }

        self.s[15] = s16;
    }

    fn generate_32bit(&mut self) -> u32 {
        self.bit_reconstruction();
        let z = self.f() ^ self.x[3];
        self.lfsr_with_work_mode();
        z
    }
}

#[cfg(test)]
mod test {
    use crate::zuc::{ZUC};

    #[test]
    fn test() {
        let key = [0u8; 16];
        let iv = [0u8; 16];
        let mut zuc = ZUC::new(&key, &iv);
        for _ in 0..10 {
            println!("{:x}", zuc.generate_32bit())
        }
    }
}

参考资料

• ZUC.pdf
• 祖冲之算法 - 维基百科，自由的百科全书