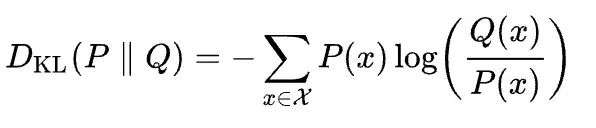编者按:当模型在生产中呈现的输入与训练期间提供的分布不对应时,通常会发生数据漂移。
Vatsal P.的这篇文章,介绍了如何通过漂移指标直观了解数据漂移程度,并n通过一个使用合成数据的例子来展示如何利用Python计算数据随时间的漂移指标。
以下是译文,Enjoy!
作者 | Vatsal P.
编译 | 岳扬
本文主要介绍了数据漂移的基本概念以及如何利用Python处理数据漂移问题。本文涉及两种计算漂移指标的方法,即交叉熵和KL散度的实现和区别。
以下是这篇文章的大纲:
- 什么是数据漂移?
- 漂移指标
2.1 交叉熵
2.2 KL散度 - 解决方案架构
程序依赖要求 - 程序实现
4.1 生成数据
4.2 训练模型
4.3 生成观察结果
4.4 计算漂移指标
4.5 随时间变化的漂移可视化 - 计算漂移指标的障碍
- 结语
1 什么是数据漂移?
MLOps是构建机器学习模型并将其部署到生产环境中的一个组成部分。数据漂移可以属于MLOps中模型监控的范畴。它指的是量化观察数据相对于训练数据的变化,这些变化随着时间的推移,会对模型的预测质量产生巨大的影响,而且往往是更糟的影响。跟踪与训练特征和预测有关的漂移指标应该是模型监测和识别模型何时应该重新训练的重要组成部分。
可以参考作者的另一篇文章(https://pub.towardsai.net/mon...),了解在生产环境中监控ML模型相关概念和架构的更多细节。
https://pub.towardsai.net/mon...
你可能不想监测与你的模型预测或模型特征相关的漂移,比如当你在进行模型预测的基础上定期重新训练模型。此为一种与时间序列模型的应用相关的常见情况。然而,你可以去追踪其他指标,以确定你所生成的模型质量。本文将主要关注那些与经典机器学习(分类、回归和聚类)相关的模型。
2 漂移指标
下文概述的两种指标都是量化概率分布相似程度的统计方法。
2.1 交叉熵
交叉熵可以通过以下公式定义:
- p:真实的概率分布
- q:估计的概率分布
从信息论的角度来看,熵反映了消除不确定性所需的信息量[3]。请注意,分布A和B的交叉熵将与分布B和A的交叉熵不同。
2.2 KL散度
Kullback Leibler散度,也称为KL散度,可以通过以下公式定义:
- P:真实的概率分布
- Q:估计的概率分布
然后,Kullback-Leibler散度是使用针对Q优化的编码而不是针对P优化的编码对P的样本进行编码所需的比特数的平均差[1]。请注意,分布A和B的KL散度与分布B和A的KL散度不同。
这两种度量都不是距离度量(distance metrics),因为这些度量缺乏对称性。
entropy / KL divergence of A,B != entropy / KL divergence of B,A3 解决方案架构
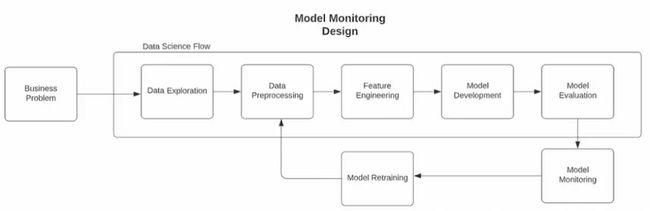
下图概述了机器学习生命周期的运行方式,同时也包括了模型监控。正如上文说明,为了监测模型的性能,应该在训练阶段保存各种数据,也就是用于训练模型的特征和目标数据。这样就可以提供一个真实的基础数据源,以便与新的观察结果进行比较。
3.1 程序依赖要求
以下Python模块及其版本是下文源代码运行的依赖。这些都是著名的数据科学/数据分析/机器学习的库,所以对大多数用户来说,安装特定的版本应该不是什么大问题。
Python=3.9.12
pandas>=1.4.3
numpy>=1.23.2
scipy>=1.9.1
matplotlib>=3.5.1
sklearn>=1.1.24 程序实现
下面将通过一个使用合成数据的例子来展示如何计算数据随时间的漂移指标。请注意,该示例生成的值不会与你操作生成的值一致,因为它们是随机生成的。此外,由于是随机生成的,所以从提供的可视化图像和数据中并不能解释结果。我们的目的是提供可重复使用和可重新配置的代码供你使用。
4.1 生成数据
import uuid
import random
import pandas as pd
import numpy as np
from scipy.stats import entropy
from matplotlib import pyplot as plt
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split
# generate data
def generate_data(n):
"""
This function will generate n rows of sample data.
params:
n (Int) : The number of rows you want to generate
returns:
A pandas dataframe with n rows.
"""
data = {
'uuid' : [str(uuid.uuid4()) for _ in range(n)],
'feature1' : [random.random() for _ in range(n)],
'feature2' : [random.random() for _ in range(n)],
'feature3' : [random.random() for _ in range(n)],
'target' : [sum([random.random(), random.random(), random.random()]) for _ in range(n)]
}
return pd.DataFrame(data)
sample_df = generate_data(1000)
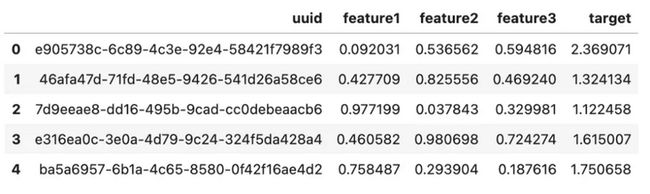
上述代码将生成一个合成数据集,该数据集由1000行和列uuid、feature1、feature2、feature3、target组成。这是我们的基础数据,模型将在此基础上进行训练。
4.2 训练模型
# train model
ft_cols = ['feature1', 'feature2', 'feature3']
X = sample_df[ft_cols].values
Y = sample_df['target'].values
X_train, X_test, y_train, y_test = train_test_split(
X, Y, test_size=0.3
)
rfr = RandomForestRegressor().fit(X_train, y_train)为了本教程的目的,上述代码允许使用者根据我们上面生成的特征和目标创建一个随机森林回归模型。假设这个模型会被推送到生产环境中,并且每天都会被调用。
4.3 生成观察结果
# generate observations
obs_df = generate_data(1500)
obs_df.drop(columns = ['target'], inplace = True)
# generate predictions
obs_df['prediction'] = obs_df[ft_cols].apply(lambda x : rfr.predict([x])[0], axis = 1)
obs_df = obs_df.rename(columns = {
'feature1' : 'obs_feature1',
'feature2' : 'obs_feature2',
'feature3' : 'obs_feature3'
})上面的代码将生成第一天与模型投入生产并被调用的特征相关观测数据。现在我们可以直观地看到真实训练数据与观测数据之间的差异。
plt.plot(sample_df['feature1'], alpha = 0.5, label = 'Ground Truth')
plt.plot(obs_df['obs_feature1'], alpha = 0.5, label = 'Observation')
plt.legend()
plt.title("Visualization of Feature1 Training Data vs Observations")
plt.show()
图片训练数据与feature1的观测数据可视化,图片由作者提供
从上图可以看出,在模型投入生产的第一天,该特征的观测值比实际情况要多。这是一个比较麻烦的问题,因为我们不能去比较两个长度不一样的数值列表。如果我们比较两个长度不同的数组,就会产生错误的结果。现在,为了计算漂移指标,我们需要使观测值的长度与真实数据的长度相等。我们可以通过创建N个buckets,并确定每个bucket中的观测值的频率来实现这一需求。其实本质上这是创建一个直方图,下面的代码片段可以显示这些分布的相互关系。
plt.hist(sample_df['feature1'], alpha = 0.5, label = 'Ground Truth', histtype = 'step')
plt.hist(obs_df['obs_feature1'], alpha = 0.5, label = 'Observation', histtype = 'step')
plt.legend()
plt.title("Feature Distribution of Ground Truth Data and Observation Data")
plt.show()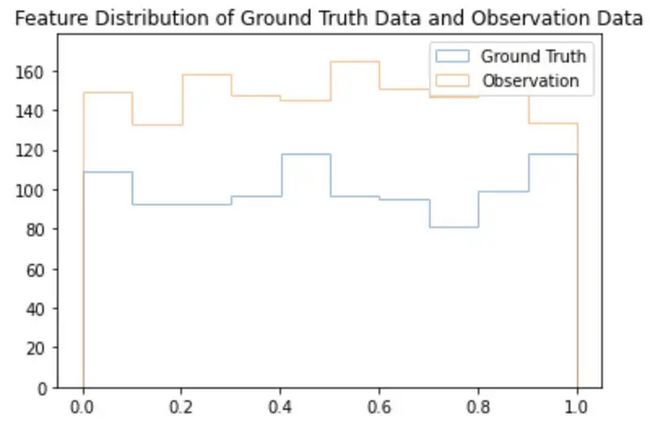
图片真实数据的特征分布与feature1的观测数据,图片由作者提供
现在两个数据集的规模相同,我们可以比较两个分布的漂移情况。
4.4 计算漂移指标
def data_length_normalizer(gt_data, obs_data, bins = 100):
"""
Data length normalizer will normalize a set of data points if they
are not the same length.
params:
gt_data (List) : The list of values associated with the training data
obs_data (List) : The list of values associated with the observations
bins (Int) : The number of bins you want to use for the distributions
returns:
The ground truth and observation data in the same length.
"""
if len(gt_data) == len(obs_data):
return gt_data, obs_data
# scale bins accordingly to data size
if (len(gt_data) > 20*bins) and (len(obs_data) > 20*bins):
bins = 10*bins
# convert into frequency based distributions
gt_hist = plt.hist(gt_data, bins = bins)[0]
obs_hist = plt.hist(obs_data, bins = bins)[0]
plt.close() # prevents plot from showing
return gt_hist, obs_hist
def softmax(vec):
"""
This function will calculate the softmax of an array, essentially it will
convert an array of values into an array of probabilities.
params:
vec (List) : A list of values you want to calculate the softmax for
returns:
A list of probabilities associated with the input vector
"""
return(np.exp(vec)/np.exp(vec).sum())
def calc_cross_entropy(p, q):
"""
This function will calculate the cross entropy for a pair of
distributions.
params:
p (List) : A discrete distribution of values
q (List) : Sequence against which the relative entropy is computed.
returns:
The calculated entropy
"""
return entropy(p,q)
def calc_drift(gt_data, obs_data, gt_col, obs_col):
"""
This function will calculate the drift of two distributions given
the drift type identifeid by the user.
params:
gt_data (DataFrame) : The dataset which holds the training information
obs_data (DataFrame) : The dataset which holds the observed information
gt_col (String) : The training data column you want to compare
obs_col (String) : The observation column you want to compare
returns:
A drift score
"""
gt_data = gt_data[gt_col].values
obs_data = obs_data[obs_col].values
# makes sure the data is same size
gt_data, obs_data = data_length_normalizer(
gt_data = gt_data,
obs_data = obs_data
)
# convert to probabilities
gt_data = softmax(gt_data)
obs_data = softmax(obs_data)
# run drift scores
drift_score = calc_cross_entropy(gt_data, obs_data)
return drift_score
calc_drift(
gt_data = sample_df,
obs_data = obs_df,
gt_col = 'feature1',
obs_col = 'obs_feature1'
)上面的代码概述了如何计算观察数据相对于训练数据的漂移(使用scipy中的entropy实现)。首先通过matplotlib中的hist方法将输入向量的大小归一化为相同的长度,通过softmax函数将这些值转换为概率,最后通过熵函数计算出漂移指标。
4.5 随时间变化的漂移指标可视化
drift_scores = {k:[] for k in ft_cols}
days = 5
for i in range(days):
# calculate drift for all features and store results
for i in ft_cols:
drift = calc_drift(
gt_data = sample_df,
obs_data = generate_data(1500),
gt_col = 'feature1',
obs_col = 'feature1'
)
drift_scores[i].append(drift)
drift_df = pd.DataFrame(drift_scores)
# visualize drift
drift_df.plot(kind = 'line')
plt.title("Drift Scores Over Time for Each Feature")
plt.ylabel("Drift Score")
plt.xlabel("Times Model Was Used")
plt.show()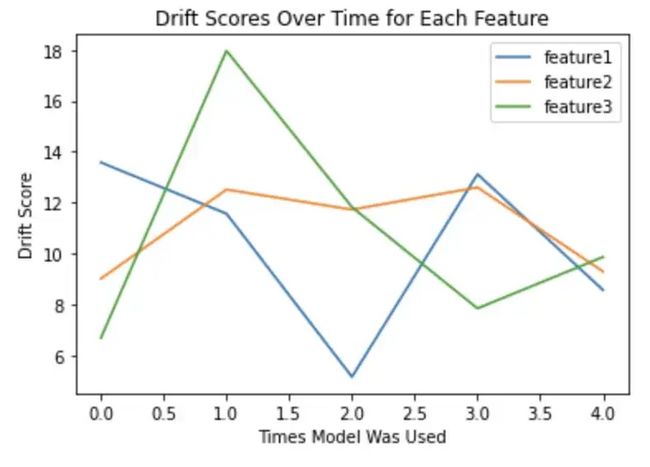
图片与模型中每个特征相关的漂移指标可视化,随模型在生产中的使用时间而变化,图片由作者提供
对基于数据集产生的结果可以设定阈值,如果模型的大多数重要特征的漂移分数超过该阈值,这将是重新训练模型的一个重要指标。对于基于树的模型,可以通过sklearn或SHAP来识别每一个特征的重要性。
5 计算漂移指标的障碍
在计算机器学习模型的数据漂移指标时,可能会遇到各种障碍:
- 处理值为0的特征值或预测值。这将产生与两个漂移实现相关的除以0的错误。对于该问题,一个快速而简单的解决方法是用一个非常接近于零的极小值来代替零。由于监测到的数据漂移可能是一种别人没有遇到的情况,所以要了解这对你正在处理的问题会产生什么影响。
- 比较一对长度不相同的分布。假设你在与每个特征和目标相关的1,000个观测值上训练模型,而每天生成预测时,根据平台获得的流量显示特征和目标的观察量从1,000到10,000不等。这明显是有问题的,因为你不能比较两个不同长度的分布。为了解决这个问题,可以使用上文代码实现中所做的分选方法,将训练数据和观测值分选成相同大小的组,然后在这些数据之上计算漂移。这种情况可以通过matplotlib库中的histogram方法轻松完成。
- 在使用softmax函数将频率转换为概率时得到NaN值。这是因为softmax函数依赖指数,在softmax的输出中得到NaN的结果是因为计算机无法计算一个大数字的指数。对于这种情况,需要另一种不使用softmax的实现方法,或者研究怎样将你传入的数值规范化,以便softmax能够工作。
6 结语
这篇文章的重点是详细介绍如何在经典机器学习的应用中计算数据漂移。本文回顾了常见的漂移计算指标(如KL Divergence和Cross Entropy)相关的原理和实现。
此外,这篇文章还概述了我们在尝试计算漂移时遇到的一些常见问题。比如当有零值时,除以零的错误和关于比较一对大小不一样的分布的问题。需要注意,这篇文章主要对那些不经常重新训练模型的人有帮助。模型监测将作为一种重要手段来衡量一个模型是否成功,并确定它的性能何时因漂移而出现退步。这两者都是重新训练或重新进入模型开发阶段的指标。
欢迎在我的GitHub页面上查看与本教程相关的资源库。(https://github.com/vatsal220/...)
参考资料
https://en.wikipedia.org/wiki...
https://en.wikipedia.org/wiki...
https://stats.stackexchange.c...
https://docs.scipy.org/doc/sc...
本文经原作者授权,由Baihai IDP编译。如需转载译文,请联系获取授权。(原文链接:https://towardsdatascience.co...)