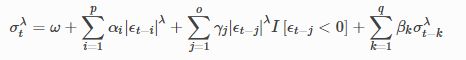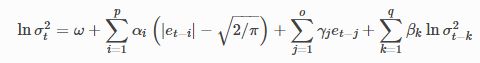关于Python的ARCH包（八）

1.7 波动率过程

波动率过程用于添加到均值模型来捕获时变的波动性。

1.7.1 常数方差

class arch.univariate.ConstantVariance[source]

常数波动率过程

注意：

模型在所有期间具有相同方差

backcast(resids)[source]

构建回测值来启动递归

Parameters:	resids (ndarray) – 残差向量 (接近)
Returns:	backcast – 在波动率递归回测中使用的值
Return type:	浮点（float）

bounds(resids)[source]

参数的收益率边界

Parameters:	resids (ndarray) – 残差向量 (接近)
Returns:	bounds –最大最小值的边界列表 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)[source]

计算ARCH模型的方差

Parameters:	parameters (ndarray) –模型参数 resids (ndarray) – 0均值方差向量 sigma2 (ndarray) – 与残差同样大小的数组，用来存储条件方差。 backcast ({float, ndarray}) – 初始化ARCH递归时使用的值.当模型包含多个组成时，可以是一个多维数组。 var_bounds (ndarray) – 包含列上下边界的数组

constraints()[source]

为参数估计构建参数约束数组

Returns:	A (ndarray) – 参数约束. 大小为约束条件个数乘以参数个数。 b (ndarray) – 约束值，对应于每一个约束条件。

注意：

构建线性非均衡约束模型时A.dot(parameters) - b >= 0，使用返回值。

simulate(parameters, nobs, rng, burn=500, initial_value=None)[source]

模拟模型数据

Parameters:	parameters ({ndarray, Series}) – 模拟波动率模型的参数 nobs (int) – 模拟的数据点 rng (callable) –可调用函数，输入为单一整型而返回一个随机向量。 burn (int, optional) – 初始化模拟时要生成的额外观察值的个数 initial_value ({float, ndarray}, optional) – 初始化模拟时使用的标量或数组
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) – 模拟方差

starting_values(resids)[source]

返回ARCH模型的起始值

Parameters:	resids (ndarray) –计算起始值时的残差数组（无偏）
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.2 GARCH

class arch.univariate.GARCH(p=1, o=0, q=1, power=2.0)[source]

GARCH以及相关的模型估计

下列模型可以使用GARCH模型时进一步具体化：

• ARCH(p)
• GARCH(p,q)
• GJR-GARCH(p,o,q)
• AVARCH(p)
• AVGARCH(p,q)
• TARCH(p,o,q)
• 主观的，预定义精度的模型

Parameters:	p (int) –对称计算的阶数 o (int) –非对称计算的阶数 q (int) –滞后条件方差（变化的）的阶数。 power (float, optional) – 计算精度，abs(e) ** power. 默认为 2.0, 这适应于ARCH 及相关模型。1.0适合 AVARCH 及相关模型。其他的精度也可以选择，但都应该严格为正，且通常大于0.25.

num_params

int – 模型参数个数。

举例：

>>> from arch.univariate import GARCH
标准 GARCH(1,1)

>>> garch = GARCH(p=1, q=1)
非对称GJR-GARCH 过程

>>> gjr = GARCH(p=1, o=1, q=1)
非对称TARCH过程

>>> tarch = GARCH(p=1, o=1, q=1, power=1.0)
注意：

在该过程类中，方差的动态变化表示如下：

 

backcast(resids)[source]

开始递归的回测值构建

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	backcast – 波动率递归中使用的回测值
Return type:	float

bounds(resids)[source]

收益率参数边界

Parameters:	resids (ndarray) –残差向量（一致）
Returns:	bounds – 边界值列表 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)[source]

计算ARCH模型的方差

Parameters:	parameters (ndarray) – 模型参数 resids (ndarray) – 0均值误差向量 sigma2 (ndarray) –存储条件方差与残差同等大小的数组 backcast ({float, ndarray}) – 初始化ARCH递归使用的值.当模型包含多个要素时可为一个多维数组。 var_bounds (ndarray) – 包含多个上下界的数组

constraints()[source]

为参数估计构建约束数组

Returns:	A (ndarray) – 约束参数，大小与参数个数一致。 b (ndarray) – 约束值，对应于每一个约束条件。

注意：

构建线性非均衡约束模型时A.dot(parameters) - b >= 0，使用返回值。

simulate(parameters, nobs, rng, burn=500, initial_value=None)[source]

模拟模型数据

Parameters:	parameters ({ndarray, Series}) – 模拟波动率模型的参数 nobs (int) – 模拟的数据点 rng (callable) –可调用函数，输入为单一整数而返回一个随机向量 burn (int, optional) – 初始化模拟时生成的额外观察值个数 initial_value ({float, ndarray}, optional) – 初始化模拟时使用的标量或数组
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) – 模拟方差

starting_values(resids)[source]

为ARCH模型返回起始值

Parameters:	resids (ndarray) – 计算起始值时使用的残差数组 (一致)
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.3 部分协整GARCH：(FI) GARCH

class arch.univariate.FIGARCH(p=1, q=1, power=2.0, truncation=1000)[source]

FIGARCH 模型

Parameters:	p ({0, 1}) – 对称项阶数 q ({0, 1}) –条件方差滞后阶数 (转换后) power (float, optional) – 计算精度, abs(e) ** power. 默认 2.0, 对应于 FIGARCH 及相关模型。 1.0对应于 FIAVARCH 及相关模型.其他精度也可以选择，但是严格为正，通常大于0.25. truncation (int, optional) – ARCH中的簇点 ARCH(∞∞) ，默认1000.

num_params

int – 模型参数个数

举例：

>>> from arch.univariate import FIGARCH
标准 FIGARCH

>>> figarch = FIGARCH()

FIARCH

>>> fiarch = FIGARCH(p=0)

FIAVGARCH 过程

>>> fiavarch = FIGARCH(power=1.0)
注意：

在该过程类中，方差变化表述如下：

 L为滞后算子，d为分布差分参数.模型使用 ARCH(∞∞)估计：

权重设置：

递归等式：

精度不是2, ARCH(∞∞) 仍旧成立。

backcast(resids)[source]

为回测开始递归计算构建值

Parameters:	resids (ndarray) – 残差向量 (一致)
Returns:	backcast – 波动性递归中回测使用的值
Return type:	float

bounds(resids)[source]

返回参数界限

Parameters:	resids (ndarray) – 残差向量 (一致)
Returns:	bounds – 参数上下界 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)[source]

计算ARCH模型方差

Parameters:	parameters (ndarray) – 模型参数 resids (ndarray) – 0均值向量 sigma2 (ndarray) –存储条件方差且与残差同等大小的数组 backcast ({float, ndarray}) – 初始化ARCH递归时使用的值，如果模型包含多项则为多维数组。 var_bounds (ndarray) – 包含上下界的列数组

constraints()[source]

为参数估计构建参数约束。

Returns:	A (ndarray) – 参数约束。大小与参数个数一致。 b (ndarray) – 约束值对应于每个约束条件。

注意：

在构建线性非均衡约束时使用了返回值： A.dot(parameters) - b >= 0

simulate(parameters, nobs, rng, burn=500, initial_value=None)[source]

模拟模型数据

Parameters:	parameters ({ndarray, Series}) – 模拟波动率模型的参数 nobs (int) –模拟数据点 rng (callable) – 可调用函数，输入为整数返回一个随机向量。 burn (int, optional) – 初始化模拟时要生成的额外观察值数。 initial_value ({float, ndarray}, optional) –初始化模拟时的标量或数组
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) – 模拟方差

starting_values(resids)[source]

返回ARCH模型的起始值l

Parameters:	resids (ndarray) – 计算起始值时的残差数组 (一致)
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.4 EGARCH

classarch.univariate.EGARCH(p=1, o=0, q=1)[source]

EGARCH 模型估计

Parameters:	p (int) – 对象项阶数 o (int) – 非对称项阶数 q (int) – 滞后条件方差阶数 (转换后)

num_params

int – 模型参数数量

举例：

>>> from arch.univariate import EGARCH
对称 EGARCH(1,1)

>>> egarch = EGARCH(p=1, q=1)
标准 EGARCH 过程

>>> egarch = EGARCH(p=1, o=1, q=1)
指数ARCH过程

>>> earch = EGARCH(p=5)
注意：

在该类中，方差变化表述如下：

backcast(resids)[source]

构建回测值来启动递归

Parameters:	resids (ndarray) –残差向量 (一致)
Returns:	backcast –波动率递归使用的值
Return type:	float

bounds(resids)[source]

返回参数上下界

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	bounds – 列出上下界 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)[source]

计算ARCH 模型方差

Parameters:	parameters (ndarray) –模型参数 resids (ndarray) – 0均值向量 sigma2 (ndarray) – 存储条件方差且与残差大小一致的数组 backcast ({float, ndarray}) – 初始化ARCH递归时使用的值.当包含多项时可以是多维数组。 var_bounds (ndarray) –包含多列上下界的数组。

constraints()[source]

构建参数约束用于参数估计

Returns:	A (ndarray) – 参数约束.大小与参数个数一致。 b (ndarray) – 约束值，对应于每个约束条件。

注意：

构建线性非均衡约束时，使用返回值的形式： A.dot(parameters) - b >= 0

simulate(parameters, nobs, rng, burn=500, initial_value=None)[source]

模拟模型数据

Parameters:	parameters ({ndarray, Series}) –用来模拟波动率模型的参数 nobs (int) – 模拟的数据点个数 rng (callable) – 可调用函数，输入为整数返回一个随机向量。 burn (int, optional) – 初始化模拟时要生成的额外观察值个数 initial_value ({float, ndarray}, optional) –初始化模拟时使用的标量或原始值数组。
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) – 模拟方差

starting_values(resids)[source]

返回ARCH模型的起始值

Parameters:	resids (ndarray) –计算起始值时的残差数组 (一致)
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.5 HARCH

class arch.univariate.HARCH(lags=1)[source]

异方差ARCH过程

Parameters:	lags ({list, array, int}) – 模型滞后阶数列表，或如为标量包括所有趋近该值的滞后阶数

num_params

int – 模型参数个数

举例：

>>> from arch.univariate import HARCH

Lag-1 HARCH,与 ARCH(1)一致

>>> harch = HARCH()

更有用且显示的滞后长度：

>>> harch = HARCH(lags=[1, 5, 22])
注意：

在一个异方差ARCH过程中，方差变化表述如下：

当滞后阶数为[1,5,22], 模型为：

HARCH过程是ARCH过程的一种特殊情况，其中一般情况下ARCH过程更为通用的参数受到限制。

backcast(resids)

构建回测值以开始递归

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	backcast –波动率递归回测时使用的值
Return type:	float

bounds(resids)[source]

返回参数上下界

Parameters:	resids (ndarray) – 参数向量 (一致)
Returns:	bounds – 上下界列表 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)[source]

计算ARCH模型的方差

Parameters:	parameters (ndarray) –模型参数 resids (ndarray) – 0均值残差向量 sigma2 (ndarray) – 存储条件方差且与残差同样大小的数组 backcast ({float, ndarray}) – 初始化ARCh递归使用的值. 当模型包含多项时可以是多维数组. var_bounds (ndarray) – 包含多列上下界数据的数组

constraints()[source]

为估计参数构建参数约束

Returns:	A (ndarray) –参数约束，大小与参数个数一致。 b (ndarray) – 约束值，对应于每一个约束条件。

注意：

构建线性非均衡约束时以该方式使用返回值：A.dot(parameters) - b >= 0

simulate(parameters, nobs, rng, burn=500, initial_value=None)[source]

模拟模型值：

Parameters:	parameters ({ndarray, Series}) –模拟波动率模型的参数 nobs (int) –模拟的数据点个数 rng (callable) – 可调用函数，输入为整数返回一个随机向量。 burn (int, optional) – 初始化模拟时要生成的额外观察值个数 initial_value ({float, ndarray}, optional) –初始化模拟时使用的标量或原始值数组。
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) – 模拟方差

starting_values(resids)[source]

返回ARCH模型的起始值

Parameters:	resids (ndarray) – 计算起始值时的残差数组（一致）
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.6 MIDAS Hyperbolic

class arch.univariate.MIDASHyperbolic(m=22, asym=False)[source]

MIDAS 双曲ARCH 过程

Parameters:	m (int) – 模型中包含的最大滞后阶长度 asym (bool) – 是否包含非对称项

num_params

int – 模型参数个数

举例：

>>> from arch.univariate import MIDASHyperbolic

22-lag MIDAS 双曲过程

>>> harch = MIDASHyperbolic()

Longer 66-period lag

>>> harch = MIDASHyperbolic(m=66)
非对称 MIDAS 双曲过程
>>> harch = MIDASHyperbolic(asym=True)
注意：

在一个 MIDAS双曲过程中，方差表述如下：

其中

参考：

[*]	Foroni, Claudia, and Massimiliano Marcellino. “A survey of Econometric Methods for Mixed-Frequency Data”. Norges Bank. (2013).

[†]	Sheppard, Kevin. “Direct volatility modeling”. Manuscript. (2018).

backcast(resids)

构建回测值以开始递归

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	backcast – 波动率递归中回测使用的值
Return type:	float

bounds(resids)[source]

Returns bounds for parameters

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	bounds –上下界列表 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)[source]

计算ARCH模型方差

Parameters:	parameters (ndarray) –模型参数 resids (ndarray) – 0均值残差向量 sigma2 (ndarray) –存储条件方差与残差同等大小的数组 backcast ({float, ndarray}) – 初始化ARCH递归使用的值，包含多项时可以是多维数组。 var_bounds (ndarray) – 包含多列上下界数据的数组。

constraints()[source]

约束

注意：

参数为(omega, alpha, gamma, theta)

A.dot(parameters) - b >= 0

1. omega >0
2. alpha>0 or alpha + gamma > 0
3. alpha<1 or alpha+0.5*gamma<1
4. theta > 0
5. theta < 1

simulate(parameters, nobs, rng, burn=500, initial_value=None)[source]

模拟模型数据

Parameters:	parameters ({ndarray, Series}) –用来模拟波动率模型的参数 nobs (int) – 模拟的数据点个数 rng (callable) – 可调用函数，输入一个整数，返回一个随机向量。 burn (int, optional) – 初始化模拟时生成的额外观察值个数。 initial_value ({float, ndarray}, optional) –初始化模拟时使用的标量或初始值数组。
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) – 模拟方差

starting_values(resids)[source]

返回ARCH模型的起始值

Parameters:	resids (ndarray) – 起算起始值时使用的残差数组（一致）
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.7 ARCH

classarch.univariate.ARCH(p=1)[source]

ARCH 过程

Parameters:	p (int) – 对称项阶数

num_params

int –模型参数个数

举例：

ARCH(1)过程

>>> from arch.univariate import ARCH

ARCH(5) 过程

>>> arch = ARCH(p=5)

注意：

方差变化表述如下：

backcast(resids)

构建回测值以开始递归

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	backcast – 波动率递归回测中使用的值。
Return type:	float

bounds(resids)

返回参数上下界

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	bounds –上下界列表 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)

计算ARCH模型方差

Parameters:	parameters (ndarray) – 模型参数 resids (ndarray) – 0均值残差向量 sigma2 (ndarray) – 存储条件方差且与残差同等大小的数组 backcast ({float, ndarray}) – 初始化ARCH递归使用的值.如包含多项则为多维数组。 var_bounds (ndarray) – 包含多个上下界列数据的数组

constraints()

为估计参数构建参数约束

Returns:	A (ndarray) – 参数约束，大小与参数个数一致。 b (ndarray) – 约束值，对应于每个约束条件。

注意：

使用返回值以该方式构建线性非均衡约束 A.dot(parameters) - b >= 0

simulate(parameters, nobs, rng, burn=500, initial_value=None)

模拟模型数据

Parameters:	parameters ({ndarray, Series}) – 模拟波动率模型的参数 nobs (int) –模拟的数据点个数 rng (callable) – 可调用函数，输入为一个整数返回一个随机向量。 burn (int, optional) – 初始化模拟时要生成的额外观察值个数 initial_value ({float, ndarray}, optional) – 初始化模拟时使用的标量或原始值数组
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) – 模拟方差

starting_values(resids)[source]

返回ARCH模型的起始值

Parameters:	resids (ndarray) –计算起始值时使用的残差数组（一致）
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.8 非参方差过程

一些波动率过程使用固定参数，因而无参数可以估计.

EWMA Variance

classarch.univariate.EWMAVariance(lam=0.94)[source]

Bases: arch.univariate.volatility.VolatilityProcess

指数加权移动平均(RiskMetrics) 方差过程

Parameters:	lam ({float, None}, optional) – 平滑参数，默认为 0.94. 若设置为none则同其他模型参数一起估计lam

num_params

int – 模型参数个数

举例：

每日 RiskMetrics EWMA 过程

>>> from arch.univariate import EWMAVariance
>>> rm = EWMAVariance(0.94)
注意：

方差动态变化表述如下：

若lam给出，既然平滑参数按固定参数对待，则该模型没有参数。设定 lam 为 None，则在拟合模型时联合估计该参数。

backcast(resids)

构建回测值以开始递归

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	backcast – 在波动率递归中回测使用的值。
Return type:	float

bounds(resids)[source]

返回参数上下界

Parameters:	resids (ndarray) –残差向量（一致）
Returns:	bounds – 上下界列表 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)[source]

计算ARCH模型方差

Parameters:	parameters (ndarray) – 模型参数 resids (ndarray) – 0均值残差模型 sigma2 (ndarray) – 存储条件方差且与残差同等大小的数组 backcast ({float, ndarray}) – 初始化ARCH递归时使用的值，如果包含多项则可以为多维数组。 var_bounds (ndarray) –包含多列上下界数据的数组

constraints()[source]

为估计参数构建参数约束

Returns:	A (ndarray) – 参数约束，大小与参数个数一致。 b (ndarray) – 约束值，对应于每个约束条件。t

注意：

使用返回值在构建线性非均衡约束时采用该形式：A.dot(parameters) - b >= 0

simulate(parameters, nobs, rng, burn=500, initial_value=None)[source]

模拟模型数据

Parameters:	parameters ({ndarray, Series}) – 模拟波动率模型的参数 nobs (int) – 模拟的数据点个数 rng (callable) – 可调用函数，输入为一个整数，返回一个随机向量。 burn (int, optional) – 初始化模拟时生成的额外观察值个数 initial_value ({float, ndarray}, optional) – 初始化模拟时使用的标量或原始值数组。
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) – 模拟方差

starting_values(resids)[source]

返回ARCH模型的起始值

Parameters:	resids (ndarray) –计算起始值时使用的残差数组（一致）
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.9 风险指标 (2006)

class arch.univariate.RiskMetrics2006(tau0=1560, tau1=4, kmax=14, rho=1.4142135623730951)[source]

Bases: arch.univariate.volatility.VolatilityProcess

RiskMetrics 2006 方差过程

Parameters:	tau0 (int, optional) – 长周期长度，默认 1560. tau1 (int, optional) – 短周期长度，默认 4. kmax (int, optional) – 因子个数，默认 14. rho (float, optional) – 毗邻周期相关度，默认 sqrt(2)

num_params

int – 模型参数个数

举例：

Daily RiskMetrics 2006 process

>>> from arch.univariate import RiskMetrics2006
>>> rm = RiskMetrics2006()
注意：

该模型的方差变化以加权平均EWMA方差过程方式呈现，平滑系数和权重分别由tau0, tau1 和 rho决定.

既然平滑参数固定，则该模型没有参数。

backcast(resids)[source]

构建回测值以开始递归

Parameters:	resids (ndarray) –残差向量（一致）
Returns:	backcast – 对应于每个EWMA项的回测值
Return type:	ndarray

bounds(resids)[source]

返回参数上下界

Parameters:	resids (ndarray) – 残差向量（一致）
Returns:	bounds – 列出每个元素上下界 (lower, upper).
Return type:	list[tuple[float,float]]

compute_variance(parameters, resids, sigma2, backcast, var_bounds)[source]

计算ARCH模型方差

Parameters:	parameters (ndarray) – 模型参数 resids (ndarray) – 0均值残差向量。 sigma2 (ndarray) –存储条件方差且与残差同等大小的数组 backcast ({float, ndarray}) –初始化ARCH递归时使用的值，如果包含多项则为多维数组。 var_bounds (ndarray) –包含多列上下界的数组

constraints()[source]

为估计参数构建参数约束。

Returns:	A (ndarray) –参数约束，大小与参数个数一致。 b (ndarray) – 约束值，对应于每个约束条件。

注意：

使用返回值在构建非均衡线性约束时以该形式构建： A.dot(parameters) - b >= 0

simulate(parameters, nobs, rng, burn=500, initial_value=None)[source]

模拟模型数据

Parameters:	parameters ({ndarray, Series}) – 模拟波动率模型的参数 nobs (int) – 模拟的数据点个数 rng (callable) – 可调用函数，输入一个整数返回一个随机向量。 burn (int, optional) –初始化模拟时生成的额外观察值个数 initial_value ({float, ndarray}, optional) – 初始化模拟时使用的标量或原始值数组
Returns:	resids (ndarray) – 模拟残差 variance (ndarray) –模拟方差

starting_values(resids)[source]

ARCH模型的收益率起始值

Parameters:	resids (ndarray) – 计算起始值时使用的残差数组（一致）
Returns:	sv – 起始值数组
Return type:	ndarray

1.7.10 固定方差

固定方差 FixedVariance class 是一个特殊用途的波动性过程，它允许'之'字形（zig-zag）的波动率过程。具体参考实例。

class arch.univariate.FixedVariance(variance, unit_scale=False)[source]

基类: arch.univariate.volatility.VolatilityProcess

固定波动率过程

Parameters:	variance ({array, Series}) –包含所用方差的数组，应该与所用数据同样大小。 unit_scale (bool, optional) – 是否采取单位比例方式计算。如果为假False，则所有参数都与方差variance成比例。反之，模型方差则为方差集。

注意：

当估计均值模型时，本类允许使用GLS方法，来使用固定不变的系列方差。

1.7.11 编写新波动率过程

所有的波动率过程必须继承自该类：class:VolatilityProcess，该类提供全部public方法.

class arch.univariate.volatility.VolatilityProcess[source]

ARCH模型的抽象基类。该类允许条件均值模型独立于条件方差，即使参数时联合估计得出的。