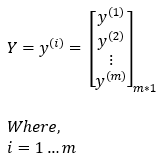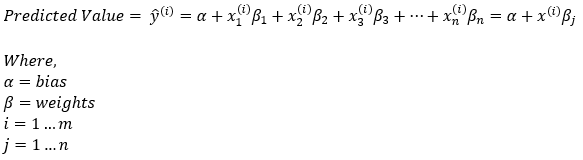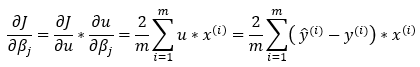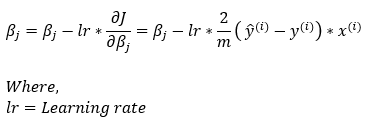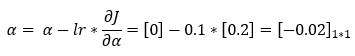梯度下降系列博客:2、梯度下降算法背后的数学直觉
推导均方误差的梯度下降算法
梯度下降系列博客:
- 梯度下降算法基础
- 梯度下降算法背后的数学直觉(你在这里!)
- 梯度下降算法及其变体
目录:
- 介绍
- 均方误差的梯度下降算法推导
- 梯度下降算法的工作示例
- 尾注
- 参考资料和资源
介绍:
欢迎!今天,我们正在努力开发一种强大的数学直觉,以了解梯度下降 算法如何为其参数找到最佳值。拥有这种感觉可以帮助您发现机器学习输出中的错误,并更加了解梯度下降 算法如何使机器学习如此强大。在接下来的几页中,我们将推导均方误差函数的梯度下降算法方程。我们将使用此博客的结果来编写梯度下降算法的代码。让我们深入研究吧!
均方误差的梯度下降算法推导:
1. 第 1 步:
输入数据显示在下面的矩阵中。在这里,我们可以观察到有**m个训练示例和n**个特征。
维度: X = (m, n)
2. 第 2 步:
预期的输出矩阵如下所示。我们预期的输出矩阵大小为**m*1,因为我们有m**个训练样本。
维度: Y = (m, 1)
3. 第 3 步:
我们将在要训练的参数中添加一个偏差元素。
![]()
维度: α = (1, 1)
4. 第 4 步:
在我们的参数中,我们有权重矩阵。权重矩阵将有**n 个元素。这里,n**是我们训练 数据集的特征数量。
维度: β = (1, n)
5. 第 5 步:
每个训练示例的预测值由下式给出,
请注意,我们正在对权重矩阵 (β) 进行转置,以使维度与矩阵乘法规则兼容。
维度: predicted_value = (1, 1) + (m, n) * (1, n)
— 对权重矩阵 (β) 进行转置 —
维度: predicted_value = (1, 1) + (m, n) * (n, 1) = (m, 1)
6. 第 6 步:
均方误差定义如下。
**维度:**成本=标量函数
7. 第 7 步:
在这种情况下,我们将使用以下梯度下降规则来确定最佳参数。
维度: α = (1, 1) & β = (1, n)
8. 第 8 步:
现在,让我们找到成本函数关于偏置元素 ( α ) 的偏导数。
维度: (1, 1)
9. 第 9 步:
现在,我们正在尝试简化上述方程以找到偏导数。
![]()
维度: u = (m, 1)
10. 第 10 步:
基于Step — 9,我们可以将成本函数写为,
**维度:**标量函数
11. 第 11 步:
接下来,我们将使用链式法则计算成本函数关于截距 ( α ) 的偏导数。
**尺寸:(**米,1)
12. 第 12 步:
接下来,我们正在计算Step_11的偏导数的第一部分。
**尺寸:(**米,1)
13. 第 13 步:
接下来,我们计算Step — 11的偏导数的第二部分。
**维度:**标量函数
14. 第 14 步:
接下来,我们将第 12步和第 13步的结果相乘,得到最终的结果。
**尺寸:(**米,1)
15. 第 15 步:
接下来,我们将使用链式法则计算成本函数关于权重 ( β ) 的偏导数。
尺寸:(1,n)
16. 第 16 步:
接下来,我们计算Step — 15的偏导数的第二部分。
**尺寸:(**米,n)
17. 第 17 步:
接下来,我们将Step_12和Step_16的结果相乘,得到最后的偏导数结果。
现在,因为我们想要有**n**个权重值,所以我们将从上面的等式中删除求和部分。
请注意,这里我们必须转置计算的第一部分,使其与矩阵乘法规则兼容。
**尺寸:(**米,1)*(米,n)
— 对错误部分进行转置 —
尺寸:(1,米)*(米,n)=(1,n)
18. 第 18 步:
接下来,我们把所有的计算值放在Step_7中,计算更新α的梯度规则 。
维度: α = (1, 1)
19. 第 19 步:
接下来,我们把所有的计算值放在Step_7中,计算出更新**β**的梯度规则 。
请注意,我们必须转置误差值以使函数与矩阵乘法规则兼容。
维度: β = (1, n) - (1, n) = (1, n)
梯度下降算法的工作示例:
现在,让我们举个例子看看梯度下降算法是如何找到最佳参数值的。
1. 第 1 步:
输入数据显示在下面的矩阵中。在这里,我们可以观察到有**4 个训练示例和2 个**特征。
2. 第 2 步:
预期的输出矩阵如下所示。我们预期的输出矩阵大小为**4*1,因为我们有4 个**训练示例。
3. 第 3 步:
我们将在要训练的参数中添加一个偏差元素。在这里,我们为偏置选择初始值 0。
4. 第 4 步:
在我们的参数中,我们有权重矩阵。权重矩阵将有 2 个元素。这里,2 是我们训练数据集的特征数量。最初,我们可以为权重矩阵选择任意随机数。
5. 第 5 步:
接下来,我们将使用输入矩阵、权重矩阵和偏差来预测值。
6. 第 6 步:
接下来,我们使用以下等式计算成本。
7. 第 7 步:
接下来,我们正在计算成本函数关于偏置元素的偏导数。我们将在梯度下降算法中使用这个结果来更新偏置参数的值。
8. 第 8 步:
接下来,我们计算成本函数关于权重矩阵的偏导数。我们将在梯度下降算法中使用这个结果来更新权重矩阵的值。
9. 第 9 步:
接下来,我们定义学习率的值。学习率是控制模型学习速度的参数。
![]()
10. 第 10 步:
接下来,我们使用梯度下降规则来更新偏置元素的参数值。
11. 第 11 步:
接下来,我们使用梯度下降规则来更新权重矩阵的参数值。
12. 第 12 步:
现在,我们重复此过程进行多次迭代,以找到最适合我们模型的参数。在每次迭代中,我们使用参数的更新值。
尾注:
因此,这就是我们如何使用均方误差的梯度下降算法找到更新规则。我们希望这能激发您的好奇心,让您渴望获得更多机器学习知识。我们将使用我们在这里推导出的规则在以后的博客中实现梯度下降算法,所以不要错过梯度下降系列的第三部分,所有这些都汇集在一起——大结局!