FCM聚类与K-means聚类的实现和对比分析
文章目录
-
- 一、收集数据
-
-
- 1.1数据来源
- 1.2数据描述
-
- 二、Fuzzy C-means
-
-
- 2.1FCM介绍
- 2.2 FCM的原理
- 2.3 FCM流程
- 2.4 对于收集的数据集的FCM代码及结果
-
- 2.4.1 代码实现
- 2.4.2 结果分析
-
- 三、K-means
-
-
-
- 3.1基本原理
- 3.2 K-means算法步骤
- 3.3 k-means的matlab代码实现和运行结果
-
- 3.3.1 代码实现
-
- 3.3.1.1 实现方法1
- 3.3.1.2 实现方法2
- 3.3.2 结果分析
-
-
- 四、两种算法的对比分析
一、收集数据
1.1数据来源
该数据来源于UCI数据库，UCI数据库是加州大学欧文分校(University of CaliforniaIrvine)提出的用于机器学习的数据库，UCI数据集是一个常用的标准测试数据集。
网址：http://archive.ics.uci.edu/ml/datasets/Solar+Flare
1.2数据描述
太阳耀斑数据集：每一类属性统计一个24小时周期太阳耀斑数据集中某一类耀斑的数量
数据量（Number of Instances）：1389
属性数量（Number of Attributes）：13（其中输入属性为10个，输出属性为3个）
1、类别代码：（A=1、B=2、C=3、D=4、E=5、F=6、H=7）
2、最大光斑尺寸代码：（X=0、R=2、S=3、A=1、H=7、K=4）
3、现场分布规范：（X=0、O=1、I=2、C=3）
4、活动（1=减少，2=不变）
5、进化（1=衰退，2=无增长，3=增长）
6、以前的24小时耀斑活动代码（1=没有M1大，2=一个M1，3=比一个M1多的活动）
7、历史复杂性（1=是，2=否）
8、在这个穿过太阳圆盘的路径上，区域是否变得历史上的复杂（1=是，2=否）
9、面积（1=小，2=大）
10、最大点面积（1=<=5，2=>5）
从所有这些属性预测三类耀斑，代表数据集中的最后三列
11、该地区在接下来的24小时内生产的C级耀斑（普通耀斑）的数量
12、该地区在接下来的24小时内产生的M级耀斑（中等耀斑）的数量
13、该地区在接下来的24小时内产生的X级耀斑（严重耀斑）的数量
二、Fuzzy C-means
2.1FCM介绍
模糊c-均值聚类算法 fuzzy c-means algorithm (FCMA)或称（ FCM）。在众多模糊聚类算法中，模糊C-均值（ FCM） 算法应用最广泛且较成功，它通过优化目标函数得到每个样本点对所有类中心的隶属度，从而决定样本点的类属以达到自动对样本数据进行分类的目的。
核心思想： 算法把n个向量xi 其中(i=1,2…,n)分为c个组Cj其中(j=1,2,…,c)，并求每组的聚类中心，使得非相似性（或距离）指标的价值函数（或目标函数）达到最小。
2.2 FCM的原理
将对象集U分成c类(2≤c≤n),则每一类都对应着一个聚类中心向量,记为 Vi=(vi1, vi2,…, vim) ,(i=1,2,…,c),以Vi作为行所构成的矩阵称为聚类中心矩阵V
FCM的目标函数：
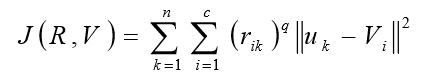
R：原矩阵
V：聚类中心
q：参数，一般可取q=2
rik：第k个样本点对于第i个类别的隶属度，一般是用两个向量之间的距离表示
||uk-Vi||：第k个样本离第i个类别的距离
第k个样本离第i个类别的距离大则隶属度就小
2.3 FCM流程
步骤1：用值在0，1间的随机数初始化隶属矩阵R(0)，使其满足约束条件，并逐步迭代
步骤2：计算对应矩阵R(l)的聚类中心V(l)
步骤3：更新隶属矩阵R(l)，比较R (l)与R (l+1)。若对取定的精度x>0,有 max{|rik (l+1) －rik (l)|} ≤ x，则R (l+1)和V (l)即为所求,即R= R (l+1), V = V (l),停止迭代。否则,l=l+1回到第2步,重复进行。
2.4 对于收集的数据集的FCM代码及结果
2.4.1 代码实现
向matlab导入txt中的数据集
（1）当数据集中存在英文时
m=1389;
n=13;
data=cell(m,n);%定义cell矩阵，存储文件内容
fid=fopen('solar.txt','r');%以只读方式打开文件
for i=1:m
for j=1:n
data{i,j}=fscanf(fid,'%s',[1,1]);%以字符方式读取每个值，遇空格完成每个值的读取
end
end
fclose (fid);
for i=1:m
for j=4:n
data{i,j}=str2double(data{i,j});%将文本格式转为数字格式
end
end
str=cell(m,1); %用于存储data的第1列
for i=1:m
str{i}=data{i,1};
end
str=cell(m,2); %用于存储data的第2列
for i=1:m
str{i}=data{i,2};
end
str=cell(m,3); %用于存储data的第3列
for i=1:m
str{i}=data{i,3};
end （2）当数据集为纯数字时
data = importdata('solar.txt');聚类实现
计算模糊熵
classF=0;%记录平均模糊熵
num_data = size(data,1);%样本个数
for i=1:3
for j=1:num_data
classF=classF+U(i,j)*log(U(i,j));
end
classF=classF/num_data;
end因为该数据集得到的是为从所有这些属性预测三类耀斑，则聚类为三类c=3
T=100;
c=3;
m=2;
[U, V]=myfcm(data, c, T, m, epsm);
function [U, V,objFcn] = myfcm(data, c, T, m, epsm)
% fuzzy c-means algorithm
% 输入： data： 待聚类数据，n行s列，n为数据个数，s为每个数据的特征数
% c ： 聚类中心个数
% m : 模糊系数
% 输出： U : 隶属度矩阵，c行n列，元素uij表示第j个数据隶属于第i类的程度
% V ： 聚类中心向量，c行s列，有c个中心，每个中心有s维特征
if nargin < 3
T = 100; %默认迭代次数为100
end
if nargin < 5
epsm = 1.0e-6; %默认收敛精度
end
if nargin < 4
m = 2; %默认模糊系数值为2
end
[n, s] = size(data);
% 初始化隶属度矩阵U(0),并归一化
U0 = rand(c, n);
temp = sum(U0,1);
for i=1:n
U0(:,i) = U0(:,i)./temp(i);
end
iter = 0;
V(c,s) = 0; U(c,n) = 0; distance(c,n) = 0;
while( iter<T )
iter = iter + 1;
% U = U0;
% 更新V(t)
Um = U0.^m;
V = Um*data./(sum(Um,2)*ones(1,s));
% 更新U(t)
for i = 1:c
for j = 1:n
distance(i,j) = mydist(data(j,:),V(i,:));
end
end
U=1./(distance.^m.*(ones(c,1)*sum(distance.^(-m))));
objFcn(iter) = sum(sum(Um.*distance.^2));
% FCM算法停止条件
if norm(U-U0,Inf)<epsm
break
end
U0=U;
end
myplot(U,objFcn);
function d = mydist(X,Y)
% 计算向量Y到向量X的欧氏距离的开方
d = sqrt(sum((X-Y).^2));
end
function myplot(U,objFcn)
% 将隶属度U矩阵可视化figure(1)
subplot(3,1,1);
plot(U(1,1:100),'-b');
title('隶属度矩阵值')
ylabel('第一类')
xlabel('样本数')
subplot(3,1,2);
plot(U(2,1:100),'-r');
ylabel('第二类')
xlabel('样本数')
subplot(3,1,3);
plot(U(3,1:100),'-g');
ylabel('第三类'）
xlabel('样本数')
title('目标函数变化值');
xlabel('迭代次数')
ylabel('目标函数值')
end
end
2.4.2 结果分析
变化迭代次数T,产生的结果也会发生改变
当T=1即迭代次数为1时
模糊熵：
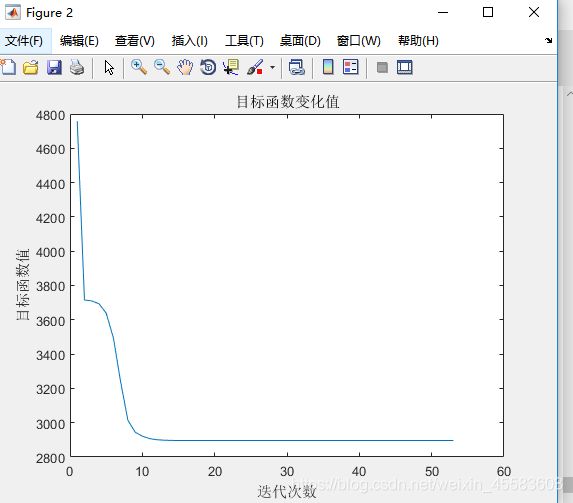
该图绘制的是目标函数J，横坐标为迭代次数，纵坐标为目标函数值。可观察出其变化趋势：目标函数Ｊ一开始迭代时，其取值大幅度下降，接着下降的幅度微弱，最后目标函数Ｊ的取值范围落在(2800-3000)之间。
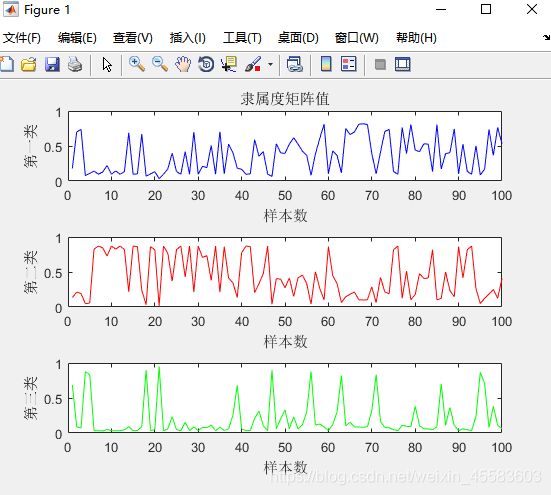
隶属度矩阵U：
隶属度矩阵可以看出每个样本对于每一个聚类的隶属程度，该图可以看出样本点1对于聚类1的隶属度为0.6868，对于聚类2隶属度为0.1788，对于聚类3的隶属度为0.1344。
聚类中心V：
聚类中心矩阵可以看出对应每一个样本中的每一个聚类中心，该图可以看出在样本1中聚类1的中心点为6.8068，聚类2的中心点为3.8093，聚类3的中心点为2.6559。
当T=2即迭代次数为2时
模糊熵：
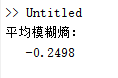
隶属度矩阵U
聚类中心矩阵V
当T=3即迭代次数为3时
模糊熵：
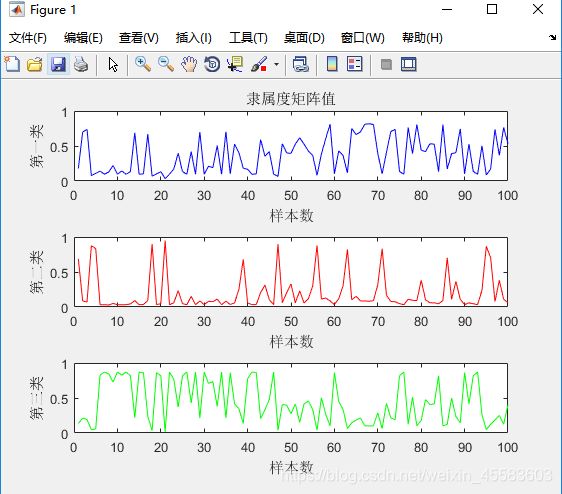
隶属度矩阵U
聚类中心矩阵V
当T=4即迭代次数为4时
当迭代次数为4时，目标函数的值显示得更具体，下降到范围（2800，2900）之间
隶属度矩阵U
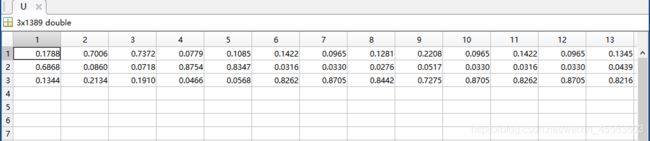聚类中心矩阵V
当T=5即迭代次数为5时
隶属度矩阵U
聚类中心矩阵V
随着迭代次数的变化，每一个样本点对每一个聚类的隶属度都在不断改变，并从目标函数得图中可以看出迭代10次后目标函数值的变换缓慢，开始收敛。
三、K-means
3.1基本原理
K-Means算法思想：对给定的数据样本集，事先确定聚类簇数K，让簇内的样本尽可能紧密分布在一起，使簇间的距离尽可能大。该算法试图使集群数据分为n组独立数据样本，使n组集群间的方差相等，数学描述为最小化惯性或集群内的平方和。K-Means作为无监督的聚类算法，实现较简单，聚类效果好，因此被广泛使用
3.2 K-means算法步骤
假设需要将收集的数据分成K类。我们需要遵循下面的几个步骤
输入：样本集D，簇的数目k，最大迭代次数N
输出：簇划分（k个簇，使平方误差最小)
1、为每个聚类选择一个初始聚类中心
2、计算剩余点到这k个中心的距离
3、将距离中心点距离最短的点归为一类(将样本集按照最小距离原则分配到最邻近聚类)
4、依次划分好所有的数据点
5、重新计算中心
6、迭代2-5 个步骤，直到中心点不会在变化为止，输出最终的聚类中心和k个簇划分
3.3 k-means的matlab代码实现和运行结果
3.3.1 代码实现
3.3.1.1 实现方法1
% 簇心数目k
K = 3;
data = importdata('solar.txt');
x = data(:,1);
y = data(:,2);
% 绘制数据，2维散点图
% x,y: 要绘制的数据点 20:散点大小相同，均为20 'blue':散点颜色为蓝色
s = scatter(x, y, 20, 'blue');
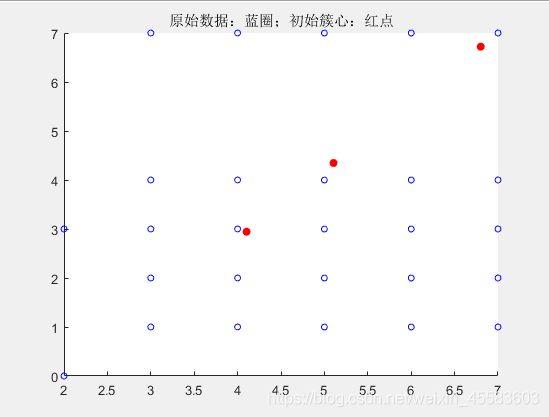
title('原始数据：蓝圈；初始簇心：红点');
% 初始化簇心
sample_num = size(data, 1); % 样本数量
sample_dimension = size(data, 2); % 每个样本特征维度
% 暂且手动指定簇心初始位置
% clusters = zeros(K, sample_dimension);
% 簇心赋初值：计算所有数据的均值，并将一些小随机向量加到均值上
clusters = zeros(K, sample_dimension);
minVal = min(data); % 各维度计算最小值
maxVal = max(data); % 各维度计算最大值
for i=1:K
clusters(i, :) = minVal + (maxVal - minVal) * rand();
end
hold on; % 在上次绘图（散点图）基础上，准备下次绘图
% 绘制初始簇心
scatter(clusters(:,1), clusters(:,2), 'red', 'filled'); % 实心圆点，表示簇心初始位置
c = zeros(sample_num, 1); % 每个样本所属簇的编号
PRECISION = 0.001;
iter = 100; % 假定最多迭代100次
% Stochastic Gradient Descendant 随机梯度下降（SGD）的K-means，也就是Competitive Learning版本
basic_eta = 1; % learning rate
for i=1:iter
pre_acc_err = 0; % 上一次迭代中，累计误差
acc_err = 0; % 累计误差
for j=1:sample_num
x_j = data(j, :); % 取得第j个样本数据，这里体现了stochastic性质
% 所有簇心和x计算距离，找到最近的一个（比较簇心到x的模长）
gg = repmat(x_j, K, 1);
gg = gg - clusters;
tt = arrayfun(@(n) norm(gg(n,:)), (1:K)');
[minVal, minIdx] = min(tt);
% 更新簇心：把最近的簇心(winner)向数据x拉动。 eta为学习率.
eta = basic_eta/i;
delta = eta*(x_j-clusters(minIdx,:));
clusters(minIdx,:) = clusters(minIdx,:) + delta;
acc_err = acc_err + norm(delta);
c(j)=minIdx;
end
if(rem(i,10) ~= 0)
continue
end
figure;
f = scatter(x, y, 20, 'blue');
hold on;
scatter(clusters(:,1), clusters(:,2), 'filled'); % 实心圆点，表示簇心初始位置
title(['第', num2str(i), '次迭代']);
if (abs(acc_err-pre_acc_err) < PRECISION)
disp(['收敛于第', num2str(i), '次迭代']);
break;
end
disp(['累计误差：', num2str(abs(acc_err-pre_acc_err))]);
pre_acc_err = acc_err;
end
disp('done');
3.3.1.2 实现方法2
%导入数据
data = importdata('solar.txt');
%计算质心
centroids = kMeans(data, 3);
%取得随机中心
function [ centroids ] = randCent( dataSet, k ) %% 取得随机中心
[m,n] = size(dataSet);%取得列数
centroids = zeros(k, n);
for j = 1:n
minJ = min(dataSet(:,j));
rangeJ = max(dataSet(:,j))-min(dataSet(:,j));
centroids(:,j) = minJ+rand(k,1)*rangeJ;%产生区间上的随机数
end
end
%计算距离
function [ dist ] = distence( vecA, vecB )
dist = (vecA-vecB)*(vecA-vecB)';%这里取欧式距离的平方
endK-means聚类
function [ subCenter,centroids ] = kMeans1( dataSet, k ) %% kMeans的核心程序，不断迭代求解聚类中心
[m,n] = size(dataSet);
%初始化聚类中心
centroids = randCent(dataSet, k);
subCenter = zeros(m,2); %做一个m*2的矩阵，第一列存储类别，第二列存储距离
change = 1;%判断是否改变
while change == 1
change = 0;
%对每一组数据计算距离
for i = 1:m
minDist = inf;
minIndex = 0;
for j = 1:k
dist= distence(dataSet(i,:), centroids(j,:));
if dist < minDist
minDist = dist;
minIndex = j;
end
end
if subCenter(i,1) ~= minIndex
change = 1;
subCenter(i,:)=[minIndex, minDist];
end
end
%对k类重新计算聚类中心
for j = 1:k
sum = zeros(1,n);
r = 0;%数量
for i = 1:m
if subCenter(i,1) == j
sum = sum + dataSet(i,:);
r = r+1;
end
end
if r~=0
centroids(j,:) = sum./r;
end
end
end
for i = 1:m
switch subCenter(i,1)
case 1
plot(dataSet(i,1), dataSet(i,2), '.b');
case 2
plot(dataSet(i,1), dataSet(i,2), '.g');
case 3
plot(dataSet(i,1), dataSet(i,2), '.r');
otherwise
plot(dataSet(i,1), dataSet(i,2), '.c');
end
end
plot(centroids(:,1),centroids(:,2),'+k');
end3.3.2 结果分析
1、方法1的运行结果分析
迭代100次的中每迭代10次的误差
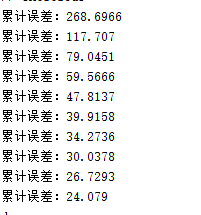
得到迭代前90次的结果
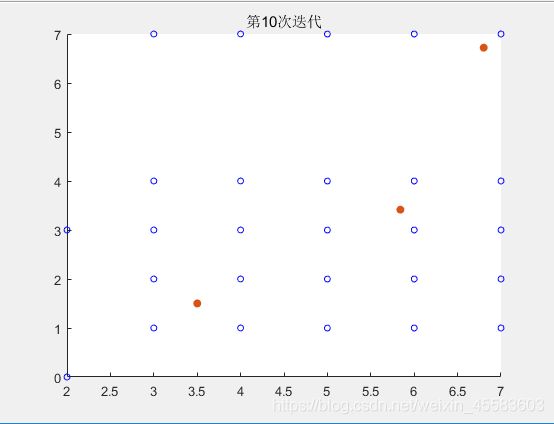
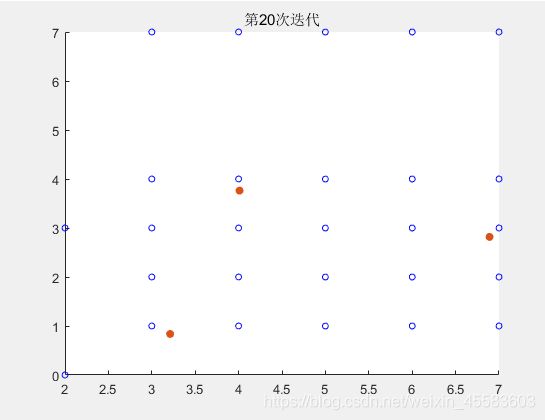
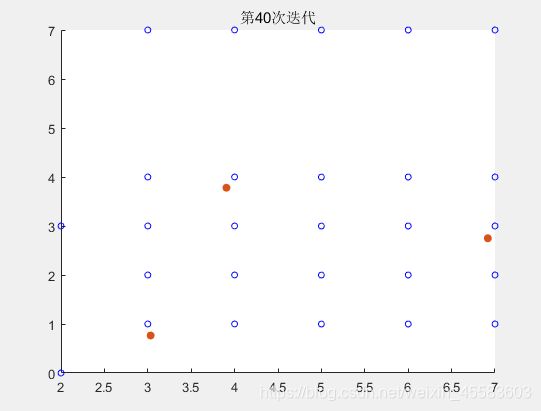
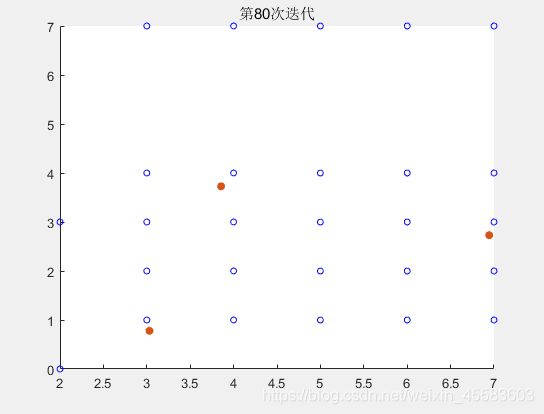
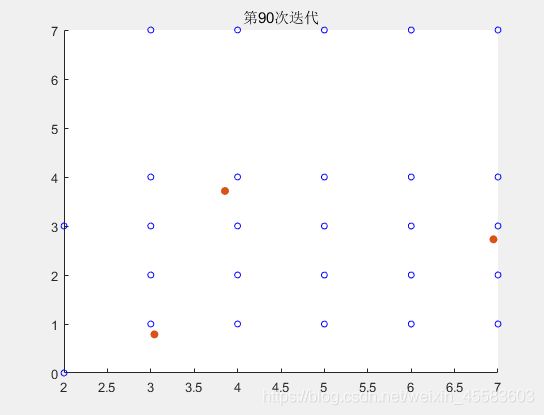
最后得到的第100次迭代的结果
2、方法2的运行结果分析
centroids表示聚类中心矩阵
subCenter表示该样本点属于哪一个聚类以及距离该聚类的聚类中心的距离
四、两种算法的对比分析
1、K均值聚类算法即是HCM（普通硬-C均值聚类算法），它是一种硬性划分的方法，结果要么是1要么是0，没有其他情况。FCM是把HCM算法推广到模糊情形，用在模糊性的分类问题上，给了隶属度一个权重。
2、K-means算法当样本集规模大时，收敛速度会变慢；对孤立点数据敏感，少量噪声就会对平均值造成较大影响；k的取值十分关键，对于不同数据集，k选择没有参考性，需要大量实验。
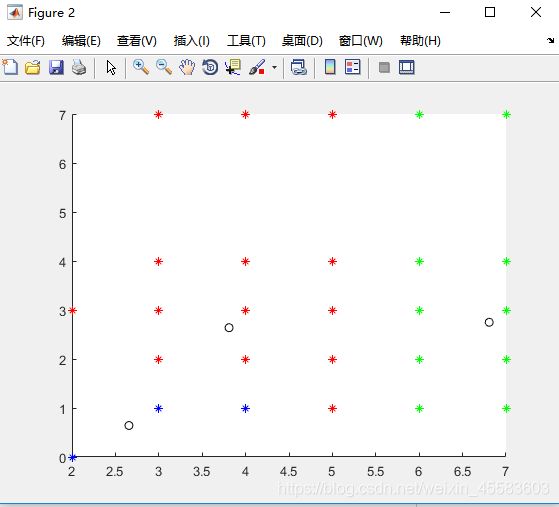
3、K-means结果
FCM结果：
从运行的精度上分析
从两个算法的结果图来看，FCM算法的分类结果的类别更加明显一点，即精度更高，
从运行的速度上分析：
K-means运用的时间
FCM运用的时间
根据运行速度结果显示：K-means算法用时4.660s，FCM算法用时0.457s，FCM算法运行的速度快于K-means算法。