DataWhale十一月组队学习“水很深的深度学习”打卡Task02
DataWhale十一月组队学习“水很深的深度学习”打卡Task02
ps:学习资料的Github地址:水很深的深度学习
DataWhale地址: 水很深的深度学习
补充资料参考:机器学习周志华(西瓜书),机器学习公式详解(南瓜书)
文章目录
- DataWhale十一月组队学习“水很深的深度学习”打卡Task02
-
- 1 机器学习
-
- 1.1 基本概念
- 1.2 数据集
- 2 误差分析
-
- 2.1 泛化误差分析
- 2.2 交叉验证
- 3 监督学习
-
- 3.1 线性回归
- 3.2 逻辑回归
- 3.3 支持向量机
- 3.4 决策树(不了解)
- 3.5 随机森林(不了解)
- 4 无监督学习
-
- 4.1 聚类
- 4.2 降维
1 机器学习
与Task1打卡内容一样,不细述
1.1 基本概念
机器学习是指让计算机具有像人一样的学习和思考能力的技术的总称。具体来说是从已知数据中获得规律,并利用规律对未知数据进行预测的技术。
机器学习分类
- 有监督学习:代表任务“分类”和“回归”
- 无监督学习:代表任务“聚类”和“降维”
- 强化学习
1.2 数据集
数据集:观测样本的集合。具体地, = 1 , 2 , ⋯ , ={_1,_2,⋯,_} D=x1,x2,⋯,xn 表示一个包含n个样本的数据集,其中 _ xi 是一个向量,表示数据集的第个样本,其维度称为样本空间的维度。
向量 _ xi 的元素称为样本的特征,其取值可以是连续的,也可以是离散的。从数据集中学出模型的过程,便称为“学习”或“训练”。
数据集的分类
- 训练集(Training set):用于模型拟合的数据样本; 类比于平时做的题目
- 验证集(Validation set):是模型训练过程中单独留出的样本集,它可以用于调整模型的超参数和用于对模型的能力进行初步评估;类比于间隔的一些小测验
- 测试集(Test set):用来评估模最终模型的泛化能力。但不能作为调参、选择特征等算法相关的选择的依据。类比于最终的考试
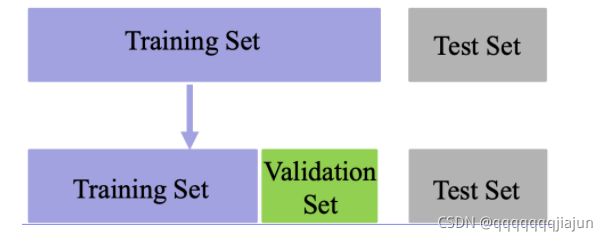
常见数据集
- 图像分类
- MNIST(手写数字) http://yann.lecun.com/exdb/mnist/
- CIFAR-10, CIFAR-100, ImageNet
- https://www.cs.toronto.edu/~kriz/cifar.html
- http://www.image-net.org/
- 电影评论情感分类
- Large Movie Review Dataset v1.0
- http://ai.stanford.edu/~amaas/data/sentiment/
- Large Movie Review Dataset v1.0
- 图像生成诗歌
- 数据集:https://github.com/researchmm/img2poem
2 误差分析
误差(error)是指算法实际预测输出与样本真实输出之间的差异。
- 模型在训练集上的误差称为“训练误差”
- 模型在总体样本上的误差称为“泛化误差”
- 模型在测试集上的误差称为“测试误差”
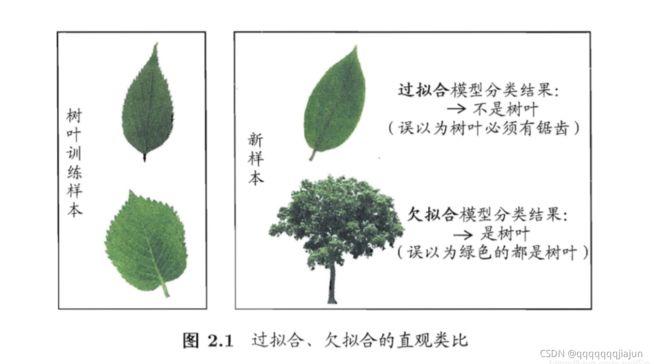
过拟合(学得太过)是指模型能很好地拟合训练样本,而无法很好地拟合测试样本的现象,从而导致泛化性能下降。为防止“过拟合”,可以选择减少参数、降低模型复杂度、正则化等
欠拟合(学得不够)是指模型还没有很好地训练出数据的一般规律,模型拟合程度不高的现象。为防止“欠拟合”,可以选择调整参数、增加迭代深度、换用更加复杂的模型等。
2.1 泛化误差分析
下面公式变形不懂的推荐看:看西瓜书P45,南瓜书P7;南瓜书公式2.41解读
假设数据集上需要预测的样本为Y,特征为X,潜在模型为 Y = f ( X ) + ε Y=f(X)+ε Y=f(X)+ε,其中 ε ∼ N ( 0 , σ ε ) ε \sim N(0,σ_ε) ε∼N(0,σε)是噪声, 估计的模型为 f ^ ( X ) \hat{f}(X) f^(X).
Err ( f ^ ) = E [ ( Y − f ^ ( X ) ) 2 ] Err ( f ^ ) = E [ ( f ( X ) + ε − f ^ ( X ) ) 2 ] Err ( f ^ ) = E [ ( f ( X ) − f ^ ( X ) ) 2 + 2 ε ( f ( X ) − f ^ ( X ) ) + ε 2 ] Err ( f ^ ) = E [ ( E ( f ^ ( X ) ) − f ( X ) + f ^ ( X ) − E ( f ^ ( X ) ) ) 2 ] + σ ε 2 Err ( f ^ ) = E [ ( E ( f ^ ( X ) ) − f ( X ) ) ] 2 + E [ ( f ^ ( X ) − E ( f ^ ( X ) ) ) 2 ] + σ ε 2 Err ( f ^ ) = Bias 2 ( f ^ ) + Var ( f ^ ) + σ ε 2 \begin{array}{l}\operatorname{Err}(\hat{f})=\mathrm{E}\left[(Y-\hat{f}(\mathrm{X}))^{2}\right] \\ \operatorname{Err}(\hat{f})=\mathrm{E}\left[(f(X)+\varepsilon-\hat{f}(\mathrm{X}))^{2}\right] \\ \operatorname{Err}(\hat{f})=\mathrm{E}\left[(f(X)-\hat{f}(\mathrm{X}))^{2}+2 \varepsilon(f(X)-\hat{f}(\mathrm{X}))+\varepsilon^{2}\right] \\ \operatorname{Err}(\hat{f})=\mathrm{E}\left[(E(\hat{f}(\mathrm{X}))-f(X)+\hat{f}(\mathrm{X})-E(\hat{f}(\mathrm{X})))^{2}\right]+\sigma_{\varepsilon}^{2} \\ \operatorname{Err}(\hat{f})=\mathrm{E}[(E(\hat{f}(\mathrm{X}))-f(X))]^{2}+\mathrm{E}\left[(\hat{f}(\mathrm{X})-E(\hat{f}(\mathrm{X})))^{2}\right]+\sigma_{\varepsilon}^{2} \\ \operatorname{Err}(\hat{f})=\operatorname{Bias}^{2}(\hat{f})+\operatorname{Var}(\hat{f})+\sigma_{\varepsilon}^{2}\end{array} Err(f^)=E[(Y−f^(X))2]Err(f^)=E[(f(X)+ε−f^(X))2]Err(f^)=E[(f(X)−f^(X))2+2ε(f(X)−f^(X))+ε2]Err(f^)=E[(E(f^(X))−f(X)+f^(X)−E(f^(X)))2]+σε2Err(f^)=E[(E(f^(X))−f(X))]2+E[(f^(X)−E(f^(X)))2]+σε2Err(f^)=Bias2(f^)+Var(f^)+σε2
其实也就是说泛化误差可分解为偏差、方差与噪声之和。
偏差(bias)反映了模型在样本上的期望输出与真实标记之间的差距,即模型本身的精准度,反映的是模型本身的拟合能力。
方差(variance)反映了同样大小的训练集的变动所导致的学习性能的变化,刻画了数据扰动所造成的影响,即模型的稳定性,反应的是模型的波动情况。
噪声:表达了在当前任务上任何学习算法所能达到的期望泛化误差的下届,即刻画了学习问题本身的难度。
为了取得好的泛化性能,则需使偏差较小,能够充分拟合数据,并且使方差较小,让数据扰动产生的影响小。

欠拟合:高偏差低方差
- 寻找更好的特征,提升对数据的刻画能力
- 增加特征数量
- 重新选择更加复杂的模型
过拟合:低偏差高方差
- 增加训练样本数量
- 减少特征维数,高维空间密度小
- 加入正则化项,使得模型更加平滑
2.2 交叉验证
3 监督学习
- 数据集有标记(答案)
- 数据集通常扩展为 ( , ) (_,_) (xi,yi),其中 ∈ Y _∈Y yi∈Y是 _ xi 的标记, Y Y Y 是所有标记的集合,称为“标记空间”或“输出空间”
- 监督学习的任务是训练出一个模型用于预测 y 的取值,根据 = { ( 1 , 1 ) , ( 2 , 2 ) , ⋯ , ( , ) } =\{(_1,_1 ),(_2,_2),⋯, (_,_)\} D={(x1,y1),(x2,y2),⋯,(xn,yn)},训练出函数,使得 ( ) ≅ ()≅ f(x)≅y
- 若预测的值是离散值,如年龄,此类学习任务称为“分类”
- 若预测的值是连续值,如房价,此类学习任务称为“回归”
3.1 线性回归
线性回归是在样本属性和标签中找到一个线性关系的方法,根据训练数据找到一个线性模型,使得模型产生的预测值与样本标签的差距最小。
3.2 逻辑回归
逻辑回归是利用函数,将线性回归产生的预测值压缩到0和1之间。此时将视作样本为正例的可能性,即
g ( f ( x k ) ) = { 1 , 1 1 + e − ( w T x k + b ) ≥ 0.5 0 , o t h e r w i s e g(f(x^k))= \left\{\begin{array}{l} 1, \frac{1}{1+e^{-(w^Tx^k+b)}}\geq 0.5 \\ 0, otherwise \end{array}\right. g(f(xk))={1,1+e−(wTxk+b)1≥0.50,otherwise
注意,逻辑回归本质上属于分类算法,sigmoid函数的具体表达形式为: g ( x ) = 1 1 + e − x g(x) = \frac{1}{1+e^{-x}} g(x)=1+e−x1.

3.3 支持向量机
推荐视频:
【五分钟机器学习】向量支持机SVM: 学霸中的战斗机
机器学习-白板推导系列(六)-支持向量机SVM
支持向量机是有监督学习中最具有影响力的方法之一,是基于线性判别函数的一种模型。
SVM基本思想:对于线性可分的数据,能将训练样本划分开的超平面有很多,于是我们寻找“位于两类训练样本正中心的超平面”, 即margin最大化。从直观上看,这种划分对训练样本局部扰动的承受性最好。事实上,这种划分的性能也表现较好。
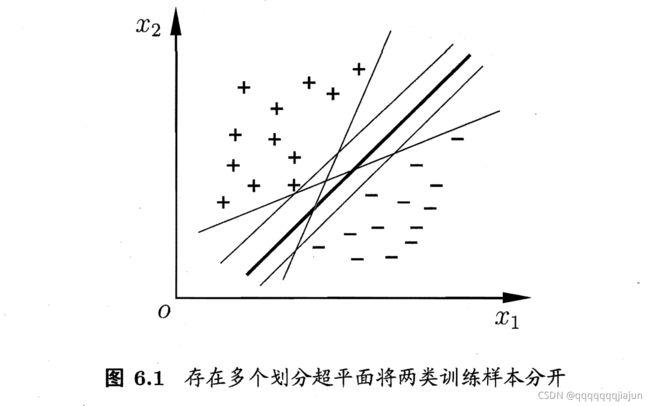
硬间隔,软间隔(容忍一些样本分类错误),核函数(将样本映射到更高维度的空间来分类)
3.4 决策树(不了解)
3.5 随机森林(不了解)
4 无监督学习
4.1 聚类
聚类的目的是将数据分成多个类别,在同一个类内,对象(实体)之间具有较高的相似性,在不同类内,对象之间具有较大的差异。
对一批没有类别标签的样本集,按照样本之间的相似程度分类,相似的归为一类,不相似的归为其它类。这种分类称为聚类分析,也称为无监督分类
常见方法有K-Means聚类、均值漂移聚类、基于密度的聚类等
4.2 降维
降维的目的就是将原始样本数据的维度降低到一个更小的数,且尽量使得样本蕴含信息量损失最小,或还原数据时产生的误差最小。比如主成分分析法…
降维的优势:
- 数据在低维下更容易处理、更容易使用;
- 相关特征,特别是重要特征更能在数据中明确的显示出来;
- 如果只有二维或者三维的话,能够进行可视化展示;
- 去除数据噪声,降低算法开销等。


