Datawhale组队学习之西瓜书task2

第三章 线性模型

3.0 机器学习三要素

1. 模型：根据具体问题，确定假设空间，选定一个模型
2. 策略：根据评价标准，确定选取最优模型的策略，确定一个损失函数
3. 优化：通过优化算法，求解损失函数，确定最优模型

3.1 基本形式

线性模型（linear model）通过给样本的每个特征不同的权重来进行建模，基本形式如下：
$$\begin{array}{rl}f(\mathbf{x})& =w_1{x}_1+w_2{x}_2+\cdots +w_d{x}_d+b\\ & ={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b\end{array}$$
需要注意的是，对于离散特征，如果存在“序”的关系（即可以进行比较），那么可以将其连续化为连续值，如果不存在“序”的关系，那么就需要转换为k维向量，比如特征“种类”的取值“A”“B”“C”转化为 (1, 0, 0), (0, 1, 0), (0, 0, 1)

接下来我们将通过线性模型来求解回归问题与分类问题

3.2 求解回归问题

3.2.1 一元线性回归

首先考虑只有一个特征的情况，现在我们已经选定了模型，接下来要确定损失函数。

对于回归问题，考虑通过最小化均方误差来确定模型参数，即
$$\begin{array}{rl}{E}_{(w,b)}& =\sum _{i=1}^m(y_i-w{x}_i-b{)}^2\\ (w^{\ast },b^{\ast })& =\underset{(w,b)}{\mathrm{argmin}}{E}_{(w,b)}\end{array}$$
现在损失函数$E$已经确定，接下来就要优化它了。

经过证明，此函数为凸函数（可以通过判断黑塞矩阵的正定性进行证明，见3.7.1），对w和b分别令偏导数等于0，可以得到最优解的解析解（闭式解）：
$$\begin{array}{rl}{w}^{\ast }& =\frac{\sum y_i(x_i-\bar{x})}{\sum x_i^2-\frac{1}{m}{\left(\sum x_i\right)}^2}\\ b^{\ast }& =\frac{1}{m}\left(\sum y_i-w{x}_i\right)\end{array}$$

这种基于均方误差最小化来进行模型求解的方法称为“最小二乘法”（least square method）

3.2.2 多元线性回归

现在考虑含有d个特征的样本，同样使用最小二乘法进行模型求解。为了便于讨论，令$\hat{\mathbf{w}}=(w_1;w_2;\cdots ;w_d;b)$，令$\widehat{{\mathbf{x}}_i}=(x_{i1};x_{i2};\cdots ;x_{id};1)$，$\mathbf{X}=({\widehat{{\mathbf{x}}_1}}^{\mathbf{T}};{\widehat{{\mathbf{x}}_2}}^{\mathbf{T}};\cdots ;{\widehat{{\mathbf{x}}_m}}^{\mathbf{T}})$，可得
$$\begin{array}{rl}({\mathbf{w}}^{\ast },b^{\ast })& =\underset{(\mathbf{w},b)}{\mathrm{argmin}}\sum _{i=1}^m(y_i-{\mathbf{w}}^{\mathbf{T}}{x}_i-b{)}^2\\ {\hat{\mathbf{w}}}^{\ast }& =\underset{\hat{\mathbf{w}}}{\mathrm{argmin}}\sum _{i=1}^m(y_i-{\hat{\mathbf{w}}}^{\mathbf{T}}{x}_i{)}^2\\ & =\underset{\hat{\mathbf{w}}}{\mathrm{argmin}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^{\mathbf{T}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})\end{array}$$
令$E_{\hat{\mathbf{w}}}=(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}}{)}^{\mathbf{T}}(\mathbf{y}-\mathbf{X}\hat{\mathbf{w}})$，同样可证明此函数为凸函数，因此令$\hat{\mathbf{w}}$的偏导数为0（向量求导见3.7.2），可得最优解：
$$\begin{array}{rl}\frac{\partial E_{\hat{\mathbf{w}}}}{\partial \hat{\mathbf{w}}}& =2{\mathbf{X}}^{\mathbf{T}}(\mathbf{X}\hat{\mathbf{w}}-\mathbf{y})=0\\ {\hat{\mathbf{w}}}^{\ast }& =({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y}\end{array}$$
显然，仅当${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$为满秩矩阵时，最优解的解析解才存在，而在现实中大多数时候该矩阵都不是满秩矩阵，常用的办法是引入正则化（regularization）项来调整学习算法的归纳偏好，从而选择最优解。

3.3 求解分类问题

对于分类问题，我们希望模型可以输出的是一个概率值，更极端的，对于二分类任务，我们希望模型只会输出0与1，因此上述会输出实数值的线性模型就不能直接使用了，我们需要改动一下模型。

3.3.1 广义线性模型

考虑单调可微函数$g(\cdot )$，令$y=g^{-1}({\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b)$，这样得到的模型即为广义线性模型（generalized linear model），函数$g(\cdot )$被称为联系函数（link function）。

通过联系函数，即便使用线性模型，也可以求取输入空间到输出空间的非线性映射

3.3.2 对数几率回归

根据分类问题的要求，我们找到了一个特殊的联系函数：
$$y=\frac{1}{1+e^{-z}}$$
此函数被称为对数几率函数（logistic function），或者Sigmoid函数，它的函数图像如下：

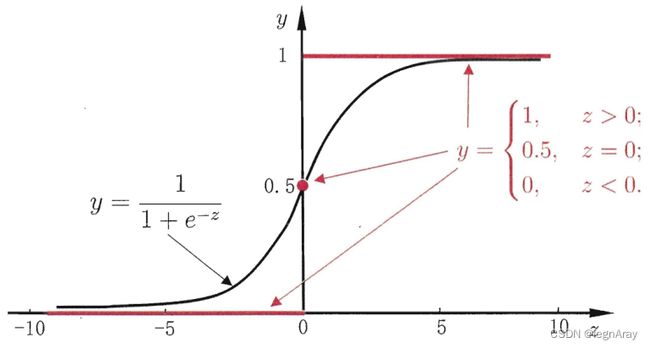
将线性模型带入对数几率函数，再小小的变化一下，得
$$\text{ln}\frac{y}{1-y}={\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b$$
$\text{ln}\frac{y}{1-y}$被我们称为对数几率（log odds），因此这种用线性回归去逼近对数几率的模型被称为对数几率回归（logistic regression）

将上式中的$y$视为概率质量函数$p(y=1|\mathbf{x})$，可得
$$\begin{array}{rl}p(y=1|\mathbf{x})& =\frac{e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}}{1+e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}}\\ p(y=0|\mathbf{x})& =\frac{1}{1+e^{{\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b}}\end{array}$$
为方便讨论，令$\mathbf{\beta }=(\mathbf{w};b),\hat{\mathbf{x}}=(\mathbf{x};1),p_1(\hat{\mathbf{x}};\mathbf{\beta })=p(y=1|\mathbf{x}),p_0(\hat{\mathbf{x}};\mathbf{\beta })=p(y=0|\mathbf{x})$

现在可以通过极大似然估计（见3.7.3）或交叉熵（见3.7.4）进行损失函数的求解，这里我选用交叉熵来求解

以单个样本$y_i$来说，理想分布$p(y_i)$与模拟分布$q(y_i)$分别是：
$$\begin{array}{rl}p(y_i)& =\{\begin{array}{ll}p(1)=1,p(0)=0& \text{ if }{y}_i=1\\ p(1)=0,p(0)=1& \text{ if }{y}_i=0\end{array}\\ q(y_i)& =\{\begin{array}{ll}{p}_1(\hat{\mathbf{x}};\mathbf{\beta })& \text{ if }{y}_i=1\\ p_0(\hat{\mathbf{x}};\mathbf{\beta })& \text{ if }{y}_i=0\end{array}\end{array}$$
因此全体训练样本的交叉熵为（令b=e）：
$$\begin{array}{rl}E(\mathbf{\beta })& =\sum _{i=1}^m\left[-\sum _{y_i}p(y_i)\text{ln}q(y_i)\right]\\ & =\sum _{i=1}^m\left[-y_i\text{ln}{p}_1(\widehat{{\mathbf{x}}_i};\mathbf{\beta })-(1-y_i)\text{ln}{p}_0(\widehat{{\mathbf{x}}_i};\mathbf{\beta })\right]\\ & =\sum _{i=1}^m\left(-y_i{\mathbf{\beta }}^{\mathbf{T}}{\hat{\mathbf{x}}}_i+\text{ln}(1+e^{{\mathbf{\beta }}^{\mathbf{T}}{\hat{\mathbf{x}}}_i})\right)\\ {\mathbf{\beta }}^{\ast }& =\underset{\mathbf{\beta }}{\mathrm{argmin}}E(\mathbf{\beta })\end{array}$$

不同于3.2中的情况，${\mathbf{\beta }}^{\ast }$没有解析解，因此需要使用一些最优化理论中的优化算法来进行求解，例如梯度下降法（gradient descent method）、牛顿法（Newton method）等，这里不做详细介绍，详情可以参见3.7.5与3.7.6

3.4 线性判别分析

线性判别分析（Linear Discriminant Analysis，LDA）是一种经典的分类方法：给定训练集，将样例投影到d维空间的直线上，使得同类样例的投影点尽可能接近、异类样例的投影点尽可能远离。

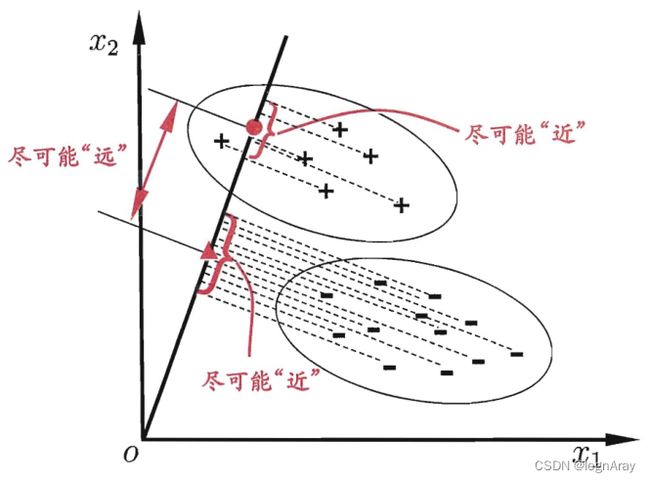
3.4.1 二分类情况

给定数据集$D=\{({\mathbf{x}}_i,y_i){\}}_{i=1}^m,y_i\in \{0,1\}$，其第$i$类（0或1）的集合、均值向量、协方差矩阵分别为$X_i,{\mathbf{\mu }}_i,{\mathbf{\Sigma }}_i$

对于均值向量，根据投影规则，可得两个投影向量为
$$\begin{array}{rl}{\mathbf{p}}_0& =\frac{\mathbf{w}}{{\mathbf{w}}^{\mathbf{T}}\mathbf{w}}{\mathbf{w}}^{\mathbf{T}}{\mathbf{\mu }}_0\\ {\mathbf{p}}_1& =\frac{\mathbf{w}}{{\mathbf{w}}^{\mathbf{T}}\mathbf{w}}{\mathbf{w}}^{\mathbf{T}}{\mathbf{\mu }}_1\end{array}$$
因此只需要留下${\mathbf{w}}^{\mathbf{T}}{\mathbf{\mu }}_0$与${\mathbf{w}}^{\mathbf{T}}{\mathbf{\mu }}_1$即可比较投影长度

而对于协方差矩阵，其投影的结果为${\mathbf{w}}^{\mathbf{T}}{\mathbf{\Sigma }}_0\mathbf{w}$与${\mathbf{w}}^{\mathbf{T}}{\mathbf{\Sigma }}_1\mathbf{w}$

定义类内散度矩阵${\mathbf{S}}_w={\mathbf{\Sigma }}_0+{\mathbf{\Sigma }}_1$，类间散度矩阵${\mathbf{S}}_b=({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)({\mathbf{\mu }}_0-{\mathbf{\mu }}_1{)}^{\mathbf{T}}$，则LDA最大化的目标
J = ∥ w T μ 0 − w T μ 1 ∥ 2 2 w T Σ 0 w + w T Σ 1 w = w T S b w w T S w w \begin{aligned} J&=\frac{\left\|\boldsymbol w^\mathbf T\boldsymbol\mu_0-\boldsymbol w^\mathbf T\boldsymbol\mu_1\right\|_2^2}{\boldsymbol w^\mathbf T\mathbf\Sigma_0\boldsymbol w+\boldsymbol w^\mathbf T\mathbf\Sigma_1\boldsymbol w} \\ &=\frac{\boldsymbol w^\mathbf T\mathbf S_b\boldsymbol w}{\boldsymbol w^\mathbf T\mathbf S_w\boldsymbol w} \end{aligned} J​=wTΣ0​w+wTΣ1​w ​wTμ0​−wTμ1​ ​22​​=wTSw​wwTSb​w​​
显而易见，$J$同时也是$S_b$对$S_w$的广义瑞利商（generalized Rayleigh quotient），其最大值可以通过最大的广义特征值确定

因为此式的解与$\mathbf{w}$的长度无关，所以我们令${\mathbf{w}}^{\mathbf{T}}{\mathbf{S}}_w\mathbf{w}=1$（仅仅是好算而已，固定哪边都行），再通过拉格朗日乘子法（见3.7.7），可以得到${\mathbf{S}}_b\mathbf{w}=\lambda S_w\mathbf{w}$（这也是广义特征值的表达式）

最终解得$\mathbf{w}={\mathbf{S}}_w^{-1}({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)$

再次提醒，我们仅仅关注$\mathbf{w}$的方向，而不关注它的大小

3.4.2 多分类情况

LDA多分类时的情况类似二分类，详细过程参见西瓜书，但归根结底还是求解$S_b$对$S_w$的广义特征值（非零），从而得到对应的特征向量

3.5 基于二分类的多分类

大多数时候，我们可以通过拆解法从而基于二分类学习器解决多分类问题

• 一对一（OvO）：将N个类别两两配对，产生$N(N-1)/2$个二分类任务，最终的结果通过每个二分类器投票产生
• 一对其余（OvR）：将一个类别作为正例，将其他类别作为反例来训练N个分类器，最终结果由置信度最大的一个分类器决定
• 多对多（MvM）：常用纠错输出码方法（ECOC），训练时编码，对N个类别进行M次划分，训练M个二分类器。测试时解码，使用M个分类器对其预测，将生成的编码与每个类别的编码比较，距离最小的即为预测结果

3.6 类别不平衡问题

对于训练样例中正反例数目不同的情况，可以通过以下三种方式处理

• 欠采样（undersampling）：也称下采样，去除一些比例高的数据
• 过采样（oversampling）：也称上采样，通过插值增加一些比例少的数据
• 阈值移动（threshold-moving）：用原始训练集训练，但在预测时令$\frac{y^{\prime }}{1-y^{\prime }}=\frac{y}{1-y}\times \frac{反例数量}{正例数量}$

3.7 补充知识

部分请点击链接查看原文…

3.7.1 凸集、凸函数与极值

3.7.2 矩阵求导

3.7.3 极大似然估计

3.7.4 交叉熵

自信息（self-information）：表示一个随机事件所包含的信息量，一个随机事件发生的概率越高，其自信息越低。
$$I(X)=-{\text{log}}_{b}p(x)$$
信息熵（entropy）：即自信息的期望，用来度量随机变量X的不确定性，信息熵越大越不确定
$$H(X)=E[I(X)]=-\sum _{x}p(x){\text{log}}_{b}p(x)$$
相对熵（relative entropy）：又称KL散度、信息散度，用来度量两个分布之间的差异，在机器学习中大多数情况是一个概率分布为真实分布，另一个为理论（拟合）分布
$$\begin{array}{rl}\text{KL}(p||q)& =\sum _{x}p(x){\text{log}}_b\frac{p(x)}{q(x)}\\ & =\sum _{x}p(x){\text{log}}_{b}p(x)-\sum _{x}p(x){\text{log}}_{b}q(x)\end{array}$$
我们把$-{\sum }_{x}p(x){\text{log}}_{b}q(x)$这一项称为交叉熵（cross-entropy），因为p分布是真实分布，那么它的信息熵是固定的，因此当我们想要最小化KL散度时，只需要最小化交叉熵即可。

3.7.5 梯度下降法

3.7.6 牛顿法

3.7.7 拉格朗日乘子法

对于仅含等式约束的优化问题
$$\begin{array}{rl}\underset{\mathbf{x}}{\min }& f(\mathbf{x})\\ \text{s.t.}& h_i(\mathbf{x})=0i=1,2,\cdots ,n\end{array}$$
若其中$f(\mathbf{x})$和$h_i(\mathbf{x})$均有连续的一阶偏导数，则可列出拉格朗日函数：
$$L(\mathbf{x},\mathbf{\lambda })=f(\mathbf{x})+\sum _{i=1}^n{\lambda }_i{h}_i(\mathbf{x})$$
对拉格朗日函数关于$\mathbf{x}$求偏导，令偏导数等于零，再结合约束条件即可解出$\mathbf{x}$，$\mathbf{x}$中包含所有可能的极值点，后续再做分析即可

---

参考资料

周志华：《机器学习》

维基百科

Datawhale：【吃瓜教程】《机器学习公式详解》（南瓜书）与西瓜书公式推导直播合集

BigYouYou：凸函数定义与判定条件 凸优化方法总论

legnAray：矩阵的迹与导数