机器学习之神经网络

神经网络介绍

传统神经网络结构比较简单，训练时随机初始化输入参数，并开启循环计算输出结果，与实际结果进行比较从而得到损失函数，并更新变量使损失函数结果值极小，当达到误差阈值时即可停止循环。

神经网络的训练目的是希望能够学习到一个模型，实现输出一个期望的目标值。学习的方式是在外界输入样本的刺激下不断改变网络的连接权值。传统神经网络主要分为一下几类：

1. 前馈型神经网络
2. 反馈型神经网络
3. 自组织神经网络

这几类网络具有不同的学习训练算法，可以归结为监督型学习算法和非监督型学习算法。

---

梯度下降算法

这个算法参考自这篇博客这个概念在神经网络中是经常需要用到的，所以在这里先进性整理…

如下：假如有一串数字1.1、1.0、1.8、2.3、2.0、2.3、2.5、3.0，请问第九个数是多少？有一个思路：先随意画一条直线，然后不断旋转它。每转一下，就分别计算一下每个样本点和直线上对应点的距离(误差)，求出所有点的误差之和。这样不断旋转，当误差之和达到最小时，停止旋转。

此时，直线在旋转一定角度停下后可得到直线的公式是y=kx+b，k代表斜率，b代表偏移值。而梯度下降法的实质是不断的修改k、b这两个参数值，使最终的误差达到最小。误差=累加(直线点-样本点)^2。

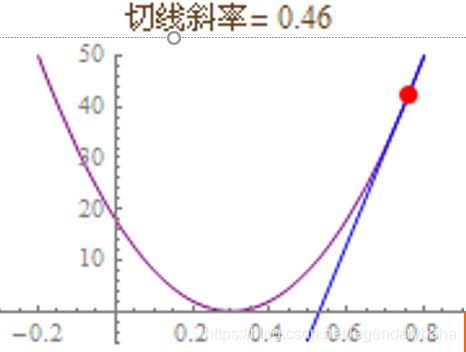
然后，根据拟合直线不断旋转的角度(斜率)和拟合的误差画一条函数曲线，如图：

于是，梯度下降的问题集中到了切线的旋转上，如图。切线旋转至水平时，切线斜率=0，即导数=0，误差降至最小值。切线每次旋转的幅度叫做学习率(Learning Rate)，加大学习率会加快拟合速度，但是如果调得太大会导致切线旋转过度而无法收敛。即梯度下降其实就是一个减小误差的过程，通过设置一定的学习率（旋转一定的角度），使得曲线沿着函数的负梯度方向下降，最后误差达到最小。

---

前馈神经网络

前馈神经网络(Feed Forward Neural Network) 是一种单向多层的网络结构，即信息是从输入层开始，逐层向一个方向传递，一直到输出层结束。

所谓的“前馈”是指输入信号的传播方向为前向，在此过程中并不调整各层的权值参数，而反传播时是将误差逐层向后传递，从而实现使用权值参数对特征的记忆，即通过反向传播(BP) 算法来计算各层网络中神经元之间边的权重。BP算法具有非线性映射能力，理论上可逼近任意连续函，从而实现对模型的学习。

---

感知器

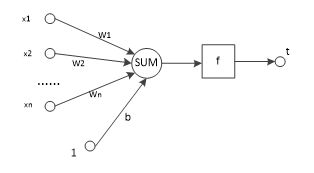
感知器是一种结构最简单的前馈神经网络，也称为感知机，它主要用于求解分类问题，一个感知器可以接收?个输入

?=(?_1,?_2,…,?_?)，对应?个权值?=(?_1,?_2,…,?_?)

此外还有一个偏置项阈值，就是图中的?，神经元将所有输入参数与对应权值进行加权求和，得到的结果经过激活函数变换后输出，计算公式如下：

?=?(?∗?+?)

而这个感知器类似于神经元，它的作用可以理解为对输入空间进行直线划分，但单层感知机无法解决最简单的非线性可分问题即异或问题。

感知器可以顺利求解与(AND，都为1才为) 和或(OR，只要1个0就为0)问题，但是对于异或(XOR，同则为1，不同为0)问题，单层感知机无法通过一条线进行分割。如上图所示，因为前面已经说了我们的感知机最主要的就是用来解决分类问题，而对于异或问题，很难将它们进行划分，于是衍生了其他的神经网络。

---

BP神经网络

BP (Back Propagation)神经网络也是前馈神经网络，只是它的参数权重值是由反向传播学习算法进行调整的。BP 神经网络模型拓扑结构包括输入层、隐层和输出层。

利用激活函数来实现从输入到输出的任意非线性映射，从而模拟各层神经元之间的交互。激活函数须满足处处可导的条件（在上面梯度下降的时候我们已经说过了，你要使得函数可以沿着某一方向不断调整下降，很显然需要处处可导，这样你的导函数才能连续）。

例如，Sigmoid函数连续可微，求导合适，单调递增，输出值是0~1之间的连续量，这些特点使其适合作为神经网络的激活函数。

它的结构如下：

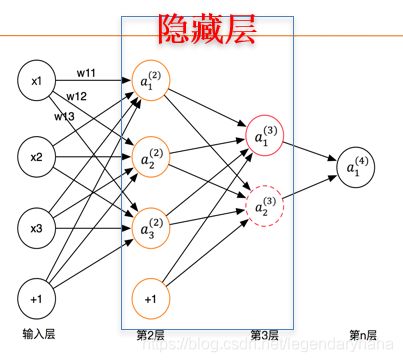
部分计算过程如下：

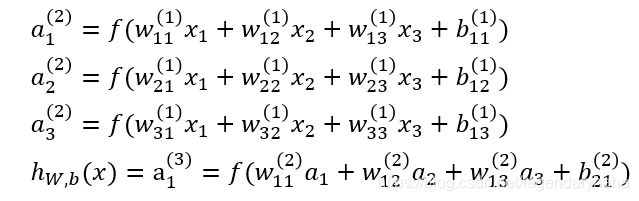
式中的?_??就是相邻两层神经元之间的权值，它们是在训练过程中需要学习的参数，而?_1^((2))中表示第2层的第1个神经元，依次类推…

a1，a2，a3分别为求出的3个神经元的输出结果，而ℎ_(?,?) (?)表示第3层第1个神经元?_1^((3))的值。

图中箭头所指的方向为前向传播的过程，即所有输入参数经过加权求和之后，将结果值依次向下一层传递，直到最后输出层，层数越多、层中神经元越多，形成的权重值参数就越多

在向前传播至第n层后，我们会输出一个预测结果，将预测结果和实际结果对比，若不符合，会进行先后传播，进行权值调整，即通过最后输出的结果来计算误差的偏导数，再用这个偏导数和前面的隐藏层进行加权求和，如此一层一层的向后传下去，直到输入层(不计算输入层)，最后利用每个节点求出的偏导数来更新权重，步骤如下：如下所示：

1. 计算每层残差：
   输出层→隐藏层：残差 = -(输出值-样本值) * 激活函数的导数
   隐藏层→隐藏层：残差 = (右层每个节点的残差加权求和)* 激活函数的导数

2. 更新权重
   输入层：权重增加 = 当前节点的Sigmoid * 右层对应节点的残差 * 学习率
   隐藏层：权重增加 = 输入值 * 右层对应节点的残差 * 学习率
   偏移值的权重增加 = 右层对应节点的残差 * 学习率

如下例子中，写出了传递过程

开始时，节点之间的权重随机生成

然后将输入节点和权值分别加权求和

然后将得到的值通过logsig函数进行映射（原来的值都是线性的，网络的逼近能力就相当有限，我们需要一种非线性的函数来使得输出结果不再是输入的线性组合，而是几乎可以逼近任意函数）
用相同的方法计算输出层：

计算误差：

根据上述公式：输出层→隐藏层的残差 = -(输出值-样本值) * 激活函数的导数，我们可以得到如下的计算（先给出导数）


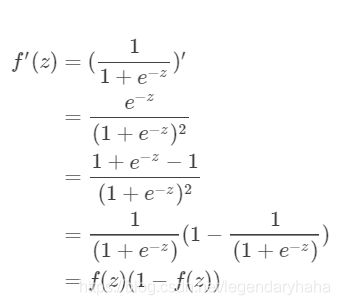
接着将输出层节点的残差加权求和

继续求隐藏层的残差：

准备更新第一层权重，此时学习率为0.6

将原来的权重和计算出来的x1,x2,x3,x4分别相加后得到更新后的权值

最后更新隐藏层和输出层之间的权重

上述过程反复迭代，通过损失函数和成本函数对前向传播结果进行判定，并通过后向传播过程对权重参数进行修正，起到监督学习的作用，一直到满足终止条件为止

---

反馈神经网络

与前馈神经网络相比，反馈神经网络内部神经元之间有反馈，可以用一个无向完全图表示，包括了Hopfield 网络、BAM网络，Elman网络等。

Hopfield网络类似人类大脑的记忆原理，即通过关联的方式，将某一件事物与周围场最中的其他事物建立关联，当人们忘记了一部分信息后，可以通过场最信息回忆起来，将缺失的信息找回。通过在反馈神经网络中引入能量函数的概念，使其运行稳定性的判断有了可靠依据，由权重值派生出能量函数是从能量高的位置向能量低的位置转化，稳定点的势能比较低。基于动力学系统理论处理状态的变换，系统的稳定态可用于描述记忆。

Hopfield网络分为离散型和连续型两种网络，在Hopfield网络中，学习算法是基于Hebb学习规则，权值调整规则为若相邻两个神经元同时处于兴奋状态，那么他们之间的连接应增强，权值增大；反之，则权值减少。

特点：

1. Hopfield是二值神经网络
2. 采用的神经元是二值神经元
3. 神经元的输出只取0和1（或-1和1），表示神经元处于激活和抑制状态
4. 单层全反馈网络，共有n个神经元 。
5. 任一神经元的输出xi均通过连接权接收所有神经元输出的反馈回来的信息，其目的就在于任何一个神经元都受到所有神经元输出的控制，从而使各神经元的输出相互制约，每个神经元均设有一个阈值Tj,目的是反映对输入的噪声的控制。

这个网络的详细理解可以看看这位博主的两篇文章

Hopfield神经网络
离散型Hopdield神经网络联想记忆功能

缺点：

1. 假记忆问题：只能记住有限个状态，并且当状态之间相似性较大时，或者状态的特征较少或不明显时，容易收敛到别的记忆上。
2. 存储容量限制：主要依赖极小点的数量。当两个样本距离较近时，就容易产生混淆，存在局部最优问题

---

自组织神经网络

才疏学浅，这个网络的详细介绍还是看看这位博主

自组织神经网络又称Kohonen网，这一神经网络的特点是当接收到外界信号刺激时，不同区域对信号自动产生不同的响应。这种神经网络是在生物神经元上首先发现的，如果神经元是同步活跃的则信号加强，如果异步活跃则信号减，比如自组织映射(SOM)网络。

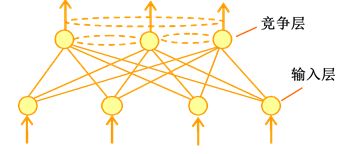
SOM网络：由输入层和竞争层组成。在一次计算中只有一个输出神经元获胜，获胜的神经元标记为1，其余神经元标记为0。主要用于完成的任务基本还是“分类”和“聚类”，前者有监督，后者无监督。

在SOM中，不仅获胜神经元要训练调整权值，它周围的神经元也要不同程度调整权向量，常见的调整方式有墨西哥草帽函数、大礼帽函数和厨师帽函数。

如图：在竞争层的节点之间是双向连接的：