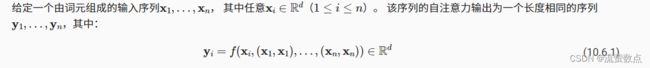自注意力和位置编码（比较卷积神经网络、循环神经网络和自注意力）
在自注意力中，查询、键和值都来自同一组输入。
卷积神经网络和自注意力都拥有并行计算的优势，而且自注意力的最大路径长度最短。但是因为其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢。
为了使用序列的顺序信息，可以通过在输入表示中添加位置编码，来注入绝对的或相对的位置信息。
参考：10.6. 自注意力和位置编码 — 动手学深度学习 2.0.0 documentation
在深度学习中，经常使用卷积神经网络（CNN）或循环神经网络（RNN）对序列进行编码。 想象一下，有了注意力机制之后，我们将词元序列输入注意力池化中， 以便同一组词元同时充当查询、键和值。 具体来说，每个查询都会关注所有的键－值对并生成一个注意力输出。 由于查询、键和值来自同一组输入，因此被称为 自注意力（self-attention） (Lin et al., 2017, Vaswani et al., 2017)， 也被称为内部注意力（intra-attention） (Cheng et al., 2016, Parikh et al., 2016, Paulus et al., 2017)。 本节将使用自注意力进行序列编码，以及如何使用序列的顺序作为补充信息。
pip install mxnet==1.7.0.post1pip install d2l==0.15.0import math
from mxnet import autograd, np, npx
from mxnet.gluon import nn
from d2l import mxnet as d2l
npx.set_np()1.自注意力
根据 (10.2.4)中定义的注意力汇聚函数f。 下面的代码片段是基于多头注意力对一个张量完成自注意力的计算， 张量的形状为（批量大小，时间步的数目或词元序列的长度，d）。 输出与输入的张量形状相同。
num_hiddens, num_heads = 100, 5
attention = d2l.MultiHeadAttention(num_hiddens, num_heads, 0.5)
attention.initialize()
batch_size, num_queries, valid_lens = 2, 4, np.array([3, 2])
X = np.ones((batch_size, num_queries, num_hiddens))
attention(X, X, X, valid_lens).shape(2, 4, 100)
2.比较卷积神经网络、循环神经网络和自注意力
接下来比较下面几个架构，目标都是将由n个词元组成的序列映射到另一个长度相等的序列，其中的每个输入词元或输出词元都由d维向量表示。具体来说，将比较的是卷积神经网络、循环神经网络和自注意力这几个架构的计算复杂性、顺序操作和最大路径长度。请注意，顺序操作会妨碍并行计算，而任意的序列位置组合之间的路径越短，则能更轻松地学习序列中的远距离依赖关系 (Hochreiter et al., 2001)。
总而言之，卷积神经网络和自注意力都拥有并行计算的优势， 而且自注意力的最大路径长度最短。 但是因为其计算复杂度是关于序列长度的二次方，所以在很长的序列中计算会非常慢。
3.位置编码
在处理词元序列时，循环神经网络是逐个的重复地处理词元的， 而自注意力则因为并行计算而放弃了顺序操作。 为了使用序列的顺序信息，通过在输入表示中添加 位置编码（positional encoding）来注入绝对的或相对的位置信息。 位置编码可以通过学习得到也可以直接固定得到。 接下来描述的是基于正弦函数和余弦函数的固定位置编码 (Vaswani et al., 2017)。
乍一看，这种基于三角函数的设计看起来很奇怪。 在解释这个设计之前，让我们先在下面的PositionalEncoding类中实现它。
#@save
class PositionalEncoding(nn.Block):
"""位置编码"""
def __init__(self, num_hiddens, dropout, max_len=1000):
super(PositionalEncoding, self).__init__()
self.dropout = nn.Dropout(dropout)
# 创建一个足够长的P
self.P = np.zeros((1, max_len, num_hiddens))
X = np.arange(max_len).reshape(-1, 1) / np.power(
10000, np.arange(0, num_hiddens, 2) / num_hiddens)
self.P[:, :, 0::2] = np.sin(X)
self.P[:, :, 1::2] = np.cos(X)
def forward(self, X):
X = X + self.P[:, :X.shape[1], :].as_in_ctx(X.ctx)
return self.dropout(X)在位置嵌入矩阵P中， 行代表词元在序列中的位置，列代表位置编码的不同维度。 从下面的例子中可以看到位置嵌入矩阵的第6列和第7列的频率高于第8列和第9列。 第6列和第7列之间的偏移量（第8列和第9列相同）是由于正弦函数和余弦函数的交替。
encoding_dim, num_steps = 32, 60
pos_encoding = PositionalEncoding(encoding_dim, 0)
pos_encoding.initialize()
X = pos_encoding(np.zeros((1, num_steps, encoding_dim)))
P = pos_encoding.P[:, :X.shape[1], :]
d2l.plot(np.arange(num_steps), P[0, :, 6:10].T, xlabel='Row (position)',
figsize=(6, 2.5), legend=["Col %d" % d for d in np.arange(6, 10)])
3.1绝对位置信息
为了明白沿着编码维度单调降低的频率与绝对位置信息的关系， 让我们打印出0,1,…,7的二进制表示形式。 正如所看到的，每个数字、每两个数字和每四个数字上的比特值 在第一个最低位、第二个最低位和第三个最低位上分别交替。
for i in range(8):
print(f'{i}的二进制是：{i:>03b}')0的二进制是：000 1的二进制是：001 2的二进制是：010 3的二进制是：011 4的二进制是：100 5的二进制是：101 6的二进制是：110 7的二进制是：111
在二进制表示中，较高比特位的交替频率低于较低比特位， 与下面的热图所示相似，只是位置编码通过使用三角函数在编码维度上降低频率。 由于输出是浮点数，因此此类连续表示比二进制表示法更节省空间。
#@save
def show_heatmaps(matrices, xlabel, ylabel, titles=None, figsize=(3.5, 4),
cmap='Blues'):
"""显示矩阵热图"""
d2l.use_svg_display()
num_rows, num_cols = matrices.shape[0], matrices.shape[1]
fig, axes = d2l.plt.subplots(num_rows, num_cols, figsize=figsize,
sharex=True, sharey=True, squeeze=False)
for i, (row_axes, row_matrices) in enumerate(zip(axes, matrices)):
for j, (ax, matrix) in enumerate(zip(row_axes, row_matrices)):
pcm = ax.imshow(matrix.asnumpy(), cmap=cmap)
if i == num_rows - 1:
ax.set_xlabel(xlabel)
if j == 0:
ax.set_ylabel(ylabel)
if titles:
ax.set_title(titles[j])
fig.colorbar(pcm, ax=axes, shrink=0.6);P = np.expand_dims(np.expand_dims(P[0, :, :], 0), 0)
show_heatmaps(P,xlabel='Column (encoding dimension)',
ylabel='Row (position)')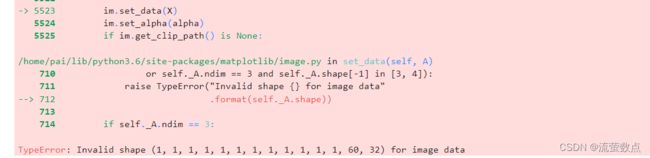
报错，然后第二天重新运行就没问题了，没搞懂，哎，代码这玩意偶尔就得放一放。。。。。
3.2相对位置信息
