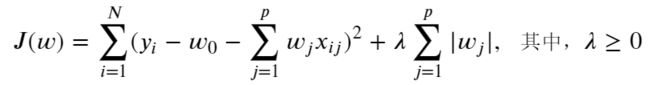集成学习03-偏差与方差理论

目录

1. 训练均方误差与测试均方误差

2. 偏差-方差的权衡

3. 估计测试误差

4. 特征提取的3种方式

5. 模型调优（针对超参数）

---

在选择基础模型后，下一步要优化模型，以达到更好的预测效果。

1. 训练均方误差与测试均方误差

对于均方误差，即：

如果我们所用的数据是训练集上的数据，那么这个误差为训练均方误差，如果我们使用测试集的数据计算的均方误差，我们称为测试均方误差。

训练模型的最终目的是使测试误差达到最小，而不是训练误差最小。

一个模型的训练均方误差最小时，不能保证测试均方误差同时也很小。模型在训练误差很小，但是测试均方误差很大时，我们称这种情况叫模型的过拟合。

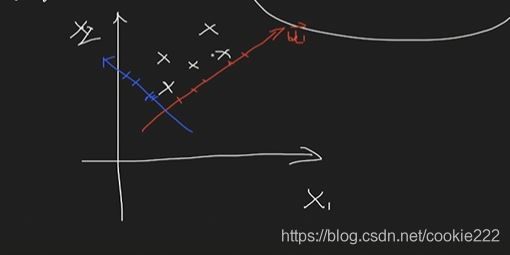
图：训练均方误差（灰色曲线），测试均方误差（红色曲线），所有方法都已使测试均方误差尽可能最小。

随着模型复杂度的升高，训练MSE持续下降，测试MSE先减小到最小值再迅速升高。

我们寻找的最优的模型是测试均方误差达到最小时对应的模型，就是训练MSE下降一点，测试MSE最小的地方，即蓝色方块的位置。

2. 偏差-方差的权衡

从上图的测试均方误差曲线可以看到：测试均方误差曲线呈现U型曲线，这表明了在测试误差曲线中有两种力量在互相博弈。可以证明：

我们称Var()为建模任务的难度，叫做不可约误差。 Var()无法控制，能进行改变的就是模型的方差和偏差。

偏差，方差的概念和意义：

所谓模型的方差就是：用不同的数据集去估计时，估计函数的改变量。一般来说，模型的复杂度越高，模型的方差就会越大。 模型的偏差是指：为了选择一个简单的模型去估计真实函数所带入的误差。偏差度量了学习算法的期望预测与真实结果的偏离程度，即刻画了学习算法本身的拟合能力。偏差度量的是单个模型的学习能力，而方差度量的是同一个模型在不同数据集上的稳定性。

方差和偏差一般是反向变化的，复杂模型方差大，偏差小；简单模型方差小，偏差大。当方差减小的量大于偏差增加的量时，模型的测试误差减小。

“偏差-方差分解”说明：泛化性能是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。

3. 估计测试误差

（1）修正训练误差：

均方误差的修改，对测试集误差的方差Var(loss_pre)添加惩罚项λ，惩罚项与特征数量成正比。这样可以减少方差，增加偏差。抑制训练误差无休止地减小，使预测的测试误差比较理想。具体的数学量：Cp, AIC, BIC。

通过训练误差进行间接估计，测试误差的估计值为使Cp达到最小的值。

（2）交叉验证：

K折交叉验证：我们把训练样本分成K等分，然后用K-1个样本集当做训练集，剩下的一份样本集为验证集去估计由K-1个样本集得到的模型的精度，这个过程重复K次取平均值得到测试误差的一个估计，5折交叉验证如下图：（蓝色的是训练集，黄色的是验证集）

4. 特征提取的3种方式

在测试误差能够被合理的估计出来以后，我们进行特征选择，使得对应的模型的测试误差的估计最小。

 （1）特征选择：从p个特征中选择m个特征，使得对应的模型的测试误差的估计最小。

• 最优子集选择
• 向前逐步选择

（2）压缩估计(正则化)：对回归的系数进行约束或者加罚，将回归系数往零的方向压缩，降低模型方差，这样也会提高模型的拟合效果。

• Lasso回归(L1正则化)
• 岭回归(L2正则化)

（3）降维：原始的特征空间对低维空间的投影，减少变量数量。

与前面介绍的两种方法不同，降维是对原始特征空间的重构。机器学习领域中所谓的降维就是指采用某种映射方法f，将原高维空间中的数据点映射到低维度的空间中。降维可用于：1）减少冗余信息所造成的误差，2）寻找数据内部的本质结构特征。在很多算法中，降维算法成为了数据预处理的一部分，如PCA。

• 主成分分析(PCA)：最大投影方差，最小重构误差

思想：通过最大投影方差 将原始空间进行重构，即由特征相关重构为无关，即落在某个方向上的点(投影)的方差最大。

5. 模型调优（针对超参数）

（1）参数与超参数：

• 参数定义了可使用的模型。
• 参数是从数据估计或获悉的。
• 参数通常不由编程者手动设置。
• 参数是机器学习算法的关键，它们通常由过去的训练数据中总结得出 。

• 超参数通常用于帮助估计模型参数。
• 超参数通常由人工指定。
• 超参数通常可以使用启发式设置。

（2）模型优化方法：

• 网格搜索GridSearchCV()
• 随机搜索 RandomizedSearchCV() 
• 贝叶斯优化

作业：
1.请用一个具体的案例解释什么是偏差和方差。
2.偏差与方差和误差之间的关系。

误差 = 方差+偏差平方+噪音方差

3.训练误差与测试误差之间的联系和区别，如何估计测试误差。
4.岭回归和lasso回归的异同点。

岭回归：

Lasso回归： 

它们都在线性回归的损失函数的基础上添加对系数的约束或者惩罚，区别是岭回归添加的是权重的平方项，Lasso回归添加的是权重的绝对值。此外，Losso能做到特征选择而岭回归却不能。
5.如果使用pca降维前是一个三维的椭球，那么把该图形降维成二维是一个什么样的图形。

圆或椭圆
6·尝试使用对偶理论和核函数对pca进行非线性拓展，使得pca变成非线性降维。（拓展题）
7.本教程讲述的三种模型简化的方法之间有什么异同点。

前面介绍的两种方法：一种是使用原始变量的子集，另一种是将变量系数压缩至零。而降维则是对原始特征空间的重构，映射为新的特征空间。
8.尝试使用sklearn，对一组数据先进行特征的简化（使用三种方式），再使用回归模型，最后使用网格搜索调参，观察三种方法的优劣。（必做）

第一部分：特征简化

(a）特征选择：方法采用向前逐步选择，衡量模型标准是AIC赤池值。

#定义向前逐步回归函数
def forward_select(data,target):
    variate=set(data.columns)  #将字段名转换成字典类型
    variate.remove(target)  #去掉因变量的字段名
    selected=[]
    current_score,best_new_score=float('inf'),float('inf')  #目前的分数和最好分数初始值都为无穷大（因为AIC越小越好）
    #循环筛选变量
    while variate:
        aic_with_variate=[]
        for candidate in variate:  #逐个遍历自变量
            formula="{}~{}".format(target,"+".join(selected+[candidate]))  #将自变量名连接起来
            aic=ols(formula=formula,data=data).fit().aic  #利用ols训练模型得出aic值
            aic_with_variate.append((aic,candidate))  #将第每一次的aic值放进空列表
        aic_with_variate.sort(reverse=True)  #降序排序aic值
        best_new_score,best_candidate=aic_with_variate.pop()  #最好的aic值等于删除列表的最后一个值，以及最好的自变量等于列表最后一个自变量
        if current_score>best_new_score:  #如果目前的aic值大于最好的aic值
            variate.remove(best_candidate)  #移除加进来的变量名，即第二次循环时，不考虑此自变量了
            selected.append(best_candidate)  #将此自变量作为加进模型中的自变量
            current_score=best_new_score  #最新的分数等于最好的分数
            print("aic is {},continuing!".format(current_score))  #输出最小的aic值
        else:
            print("for selection over!")
            break
    formula="{}~{}".format(target,"+".join(selected))  #最终的模型式子
    print("final formula is {}".format(formula))
    model=ols(formula=formula,data=data).fit()
    return model

import pandas as pd
from sklearn.datasets import fetch_california_housing as fch  #加载加利福尼亚房屋价值数据
from statsmodels.formula.api import ols #加载普通最小二乘模型
data=fch() #导入数据
house_data=pd.DataFrame(data.data) #将自变量转换成dataframe格式，便于查看
house_data.columns=data.feature_names  #命名自变量
house_data.loc[:,"value"]=data.target #合并自变量，因变量数据
house_data.shape #查看数据量
house_data.head(10) #查看前10行数据
#分训练集测试集
import random
random.seed(123) #设立随机数种子
a=random.sample(range(len(house_data)),round(len(house_data)*0.3))
house_test=[]
for i in a:
    house_test.append(house_data.iloc[i])
house_test=pd.DataFrame(house_test)
house_train=house_data.drop(a)
#调用向前逐步选择函数
model = forward_select(data=house_train,target="value")
print(model)

(b)  压缩估计：简单的岭回归、Lasso回归。

from sklearn import datasets, linear_model
import numpy as np

boston = datasets.load_boston()
X = boston.data
y = boston.target
# 岭回归
reg_rid = linear_model.Ridge(alpha=.5)
reg_rid.fit(X,y)
L2_score = reg_rid.score(X,y)
print("L2_score is: ", L2_score)
# Lasso回归
reg_lasso = linear_model.Lasso(alpha = 0.5)
reg_lasso.fit(X,y)
L1_score = reg_lasso.score(X,y)
print("L1_score is: ", L1_score)

(c)  降维：这里采用PCA。

def my_pca(X, d):
    # Centralization
    means = np.mean(X, 0)
    X = X - means
    # Covariance Matrix
    covM = np.dot(X.T, X)
    eigval, eigvec = np.linalg.eig(covM)
    indexes = np.argsort(eigval)[-d:]
    W = eigvec[:, indexes]
    return np.dot(X, W)

from sklearn import datasets
from sklearn.decomposition import PCA
import numpy as np
import matplotlib.pyplot as plt
from sklearn.cluster import KMeans

iris = datasets.load_iris()
X = iris.data
# 调用sklearn官方库
X_reduced = PCA(n_components=2).fit_transform(iris.data)
kmeans = KMeans(n_clusters=3).fit(X_reduced)
plt.subplot(121)
plt.scatter(X_reduced[:, 0], X_reduced[:, 1], c=kmeans.labels_, cmap=plt.cm.Set1)
# 调用my_pca()函数
X_pca = my_pca(iris.data, 2)
kmeans = KMeans(n_clusters=3).fit(X_pca)
plt.subplot(122)
plt.scatter(X_pca[:, 0], X_pca[:, 1], c=kmeans.labels_, cmap=plt.cm.Set1)
plt.show()

 第二部分：模型调参：网格搜索、随机搜索。

 使用SVR（支持向量回归）的例子，结合管道来进行调优。

# 我们先来对未调参的SVR进行评价：
from sklearn.svm import SVR     # 引入SVR类
from sklearn.pipeline import make_pipeline   # 引入管道简化学习流程
from sklearn.preprocessing import StandardScaler # 由于SVR基于距离计算，引入对数据进行标准化的类
from sklearn.model_selection import GridSearchCV  # 引入网格搜索调优
from sklearn.model_selection import cross_val_score # 引入K折交叉验证
from sklearn import datasets
import numpy as np

boston = datasets.load_boston()     # 返回一个类似于字典的类
X = boston.data
y = boston.target
features = boston.feature_names
pipe_SVR = make_pipeline(StandardScaler(),
                                                         SVR())
score1 = cross_val_score(estimator=pipe_SVR,
                                                     X = X,
                                                     y = y,
                                                     scoring = 'r2',
                                                      cv = 10)       # 10折交叉验证
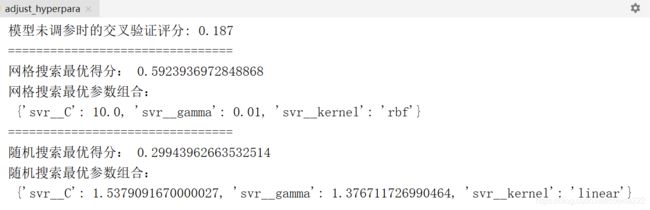
print("模型未调参时的交叉验证评分: %.3f" % ((np.mean(score1))))

# 下面我们使用网格搜索来对SVR调参：
from sklearn.pipeline import Pipeline
pipe_svr = Pipeline([("StandardScaler",StandardScaler()),
                                                         ("svr",SVR())])
param_range = [0.01,0.1,1.0,10.0,100.0]
param_grid = [{"svr__C":param_range,"svr__kernel":["linear"]},  # 注意__是指两个下划线，一个下划线会报错的
                            {"svr__C":param_range,"svr__gamma":param_range,"svr__kernel":["rbf"]}]
gs = GridSearchCV(estimator=pipe_svr,
                                                     param_grid = param_grid,
                                                     scoring = 'r2',
                                                      cv = 10)       # 10折交叉验证
gs = gs.fit(X,y)
print("================================")
print("网格搜索最优得分：",gs.best_score_)
print("网格搜索最优参数组合：\n",gs.best_params_)

# 下面我们使用随机搜索来对SVR调参：
from sklearn.model_selection import RandomizedSearchCV
from scipy.stats import uniform  # 引入均匀分布设置参数
pipe_svr = Pipeline([("StandardScaler",StandardScaler()),
                                                         ("svr",SVR())])
distributions = dict(svr__C=uniform(loc=1.0, scale=4),    # 构建连续参数的分布
                     svr__kernel=["linear","rbf"],                                   # 离散参数的集合
                    svr__gamma=uniform(loc=0, scale=4))

rs = RandomizedSearchCV(estimator=pipe_svr,
                                                     param_distributions = distributions,
                                                     scoring = 'r2',
                                                      cv = 10)       # 10折交叉验证
rs = rs.fit(X,y)
print("================================")
print("随机搜索最优得分：",rs.best_score_)
print("随机搜索最优参数组合：\n",rs.best_params_)