机器学习术语表

本术语表中列出了一般的机器学习术语和 TensorFlow 专用术语的定义。
以下内容可下载:https://download.csdn.net/download/bigdata_wangzhe/15543442

A

A/B 测试 (A/B testing)

一种统计方法，用于将两种或多种技术进行比较，通常是将当前采用的技术与新技术进行比
较。A/B 测试不仅旨在确定哪种技术的效果更好，而且还有助于了解相应差异是否具有显著
的统计意义。A/B 测试通常是采用一种衡量方式对两种技术进行比较，但也适用于任意有限
数量的技术和衡量方式。

准确率 (accuracy)

分类模型 (#classi¦cation_model)的正确预测所占的比例。在多类别分类 (#multi-class)中，准确
率的定义如下：

在二元分类 (#binary_classi¦cation)中，准确率的定义如下：

请参阅正例 (#TP)和负例 (#TN)。

激活函数 (activation function)

一种函数（例如 ReLU (#ReLU) 或 S 型函数 (#sigmoid_function)），用于对上一层的所有输入求加权和，然后生成一个输出值（通常为非线性值），并将其传递给下一层。

AdaGrad

一种先进的梯度下降法，用于重新调整每个参数的梯度，以便有效地为每个参数指定独立的
学习速率 (#learning_rate)。如需查看完整的解释，请参阅这篇论文
(http://www.jmlr.org/papers/volume12/duchi11a/duchi11a.pdf)。

ROC 曲线下面积 (AUC, Area under the ROC Curve)

一种会考虑所有可能分类阈值 (#classi¦cation_threshold)的评估指标。
ROC 曲线 (#ROC)下面积是，对于随机选择的正类别样本确实为正类别，以及随机选择的负类
别样本为正类别，分类器更确信前者的概率。

B

反向传播算法 (backpropagation)

在神经网络 (#neural_network)上执行梯度下降法 (#gradient_descent)的主要算法。该算法会先按前向传播方式计算（并缓存）每个节点的输出值，然后再按反向传播遍历图的方式计算损失
函数值相对于每个参数的偏导数 (https://en.wikipedia.org/wiki/Partial_derivative)。

基准 (baseline)

一种简单的模型 (#model)或启发法，用作比较模型效果时的参考点。基准有助于模型开发者
针对特定问题量化最低预期效果。

批次 (batch)

模型训练 (#model_training)的一次迭代 (#iteration)（即一次梯度 (#gradient)更新）中使用的样本
集。

批次大小 (batch size)

一个批次 (#batch)中的样本数。例如，SGD (#SGD) 的批次大小为 1，而小批次 (#mini-batch)的
大小通常介于 10 到 1000 之间。批次大小在训练和推断期间通常是固定的；不过，
TensorFlow 允许使用动态批次大小。

偏差 (bias)

距离原点的截距或偏移。偏差（也称为偏差项）在机器学习模型中用 b 或 w0 表示。例如，
在下面的公式中，偏差为 b：

请勿与预测偏差 (#prediction_bias)混淆。

二元分类 (binary classi‹cation)

一种分类任务，可输出两种互斥类别之一。例如，对电子邮件进行评估并输出“垃圾邮
件”或“非垃圾邮件”的机器学习模型就是一个二元分类器。

分箱 (binning)

请参阅分桶 (#bucketing)。

分桶 (bucketing)

将一个特征（通常是连续 (#continuous_feature)特征）转换成多个二元特征（称为桶或箱），
通常根据值区间进行转换。例如，您可以将温度区间分割为离散分箱，而不是将温度表示成
单个连续的浮点特征。假设温度数据可精确到小数点后一位，则可以将介于 0.0 到 15.0 度之
间的所有温度都归入一个分箱，将介于 15.1 到 30.0 度之间的所有温度归入第二个分箱，并
将介于 30.1 到 50.0 度之间的所有温度归入第三个分箱。

C

校准层 (calibration layer)

一种预测后调整，通常是为了降低预测偏差 (#prediction_bias)的影响。调整后的预测和概率应
与观察到的标签集的分布一致。

候选采样 (candidate sampling)

一种训练时进行的优化，会使用某种函数（例如 softmax）针对所有正类别标签计算概率，
但对于负类别标签，则仅针对其随机样本计算概率。例如，如果某个样本的标签为“小猎
犬”和“狗”，则候选采样将针对“小猎犬”和“狗”类别输出以及其他类别（猫、棒棒糖、栅栏）的
随机子集计算预测概率和相应的损失项。这种采样基于的想法是，只要正类别
(#positive_class)始终得到适当的正增强，负类别 (#negative_class)就可以从频率较低的负增强
中进行学习，这确实是在实际中观察到的情况。候选采样的目的是，通过不针对所有负类别
计算预测结果来提高计算效率。

分类数据 (categorical data)

一种特征 (#feature)，拥有一组离散的可能值。以某个名为 house style 的分类特征为例，该
特征拥有一组离散的可能值（共三个），即 Tudor, ranch, colonial。通过将 house style 表示成分类数据，相应模型可以学习 Tudor、ranch 和 colonial 分别对房价的影
响。
有时，离散集中的值是互斥的，只能将其中一个值应用于指定样本。例如，car maker 分类
特征可能只允许一个样本有一个值 (Toyota)。在其他情况下，则可以应用多个值。一辆车可
能会被喷涂多种不同的颜色，因此，car color 分类特征可能会允许单个样本具有多个值
（例如 red 和 white）。
分类特征有时称为离散特征 (#discrete_feature)。 与数值数据 (#numerical_data)相对。

形心 (centroid)

聚类的中心，由 k-means (#k-means) 或 k-median (#k-median) 算法决定。例如，如果 k 为 3，则 k-means 或 k-median 算法会找出 3 个形心。

检查点 (checkpoint)

一种数据，用于捕获模型变量在特定时间的状态。借助检查点，可以导出模型权重 (#weight)
，跨多个会话执行训练，以及使训练在发生错误之后得以继续（例如作业抢占）。请注意，
图 (#graph)本身不包含在检查点中。

类别 (class)

为标签枚举的一组目标值中的一个。例如，在检测垃圾邮件的二元分类 (#binary_classi¦cation)
模型中，两种类别分别是“垃圾邮件”和“非垃圾邮件”。在识别狗品种的多类别分类
(#multi_class_classi¦cation)模型中，类别可以是“贵宾犬”、“小猎犬”、“哈巴犬”等等。

分类不平衡的数据集 (class-imbalanced data set)

分类不平衡的数据集 (class-imbalanced data set)

一种二元分类 (#binary_classi¦cation)问题，在此类问题中，两种类别的标签 (#label)在出现频率
方面具有很大的差距。例如，在某个疾病数据集中，0.0001 的样本具有正类别标签，0.9999
的样本具有负类别标签，这就属于分类不平衡问题；但在某个足球比赛预测器中，0.51 的样
本的标签为其中一个球队赢，0.49 的样本的标签为另一个球队赢，这就不属于分类不平衡问
题。

分类模型 (classi‹cation model)

一种机器学习模型，用于区分两种或多种离散类别。例如，某个自然语言处理分类模型可以
确定输入的句子是法语、西班牙语还是意大利语。请与回归模型 (#regression_model)进行比
较。

分类阈值 (classi‹cation threshold)

一种标量值条件，应用于模型预测的得分，旨在将正类别 (#positive_class)与负类别
(#negative_class)区分开。将逻辑回归 (#logistic_regression)结果映射到二元分类
(#binary_classi¦cation)时使用。以某个逻辑回归模型为例，该模型用于确定指定电子邮件是垃
圾邮件的概率。如果分类阈值为 0.9，那么逻辑回归值高于 0.9 的电子邮件将被归类为“垃圾
邮件”，低于 0.9 的则被归类为“非垃圾邮件”。

聚类 (clustering)

将关联的样本 (#example)分成一组，一般用于非监督式学习 (#unsupervised_machine_learning)。
在所有样本均分组完毕后，相关人员便可选择性地为每个聚类赋予含义。
聚类算法有很多。例如，k-means (#k-means) 算法会基于样本与形心 (#centroid)的接近程度聚
类样本，如下图所示：

之后，研究人员便可查看这些聚类并进行其他操作，例如，将聚类 1 标记为“矮型树”，将聚
类 2 标记为“全尺寸树”。
再举一个例子，例如基于样本与中心点距离的聚类算法，如下所示：

协同过滤 (collaborative ‹ltering)

根据很多其他用户的兴趣来预测某位用户的兴趣。协同过滤通常用在推荐系统中。

混淆矩阵 (confusion matrix)

一种 NxN 表格，用于总结分类模型 (#classi¦cation_model)的预测效果；即标签和模型预测的
分类之间的关联。在混淆矩阵中，一个轴表示模型预测的标签，另一个轴表示实际标签。N
表示类别个数。在二元分类 (#binary_classi¦cation)问题中，N=2。例如，下面显示了一个二元
分类问题的混淆矩阵示例：

上面的混淆矩阵显示，在 19 个实际有肿瘤的样本中，该模型正确地将 18 个归类为有肿瘤
（18 个正例），错误地将 1 个归类为没有肿瘤（1 个假负例）。同样，在 458 个实际没有肿
瘤的样本中，模型归类正确的有 452 个（452 个负例），归类错误的有 6 个（6 个假正
例）。
多类别分类问题的混淆矩阵有助于确定出错模式。例如，某个混淆矩阵可以揭示，某个经过
训练以识别手写数字的模型往往会将 4 错误地预测为 9，将 7 错误地预测为 1。
混淆矩阵包含计算各种效果指标（包括精确率 (#precision)和召回率 (#recall)）所需的充足信
息。

连续特征 (continuous feature)

一种浮点特征，可能值的区间不受限制。与离散特征 (#discrete_feature)相对。

收敛 (convergence)

通俗来说，收敛通常是指在训练期间达到的一种状态，即经过一定次数的迭代之后，训练损 失 (#loss)和验证损失在每次迭代中的变化都非常小或根本没有变化。也就是说，如果采用当
前数据进行额外的训练将无法改进模型，模型即达到收敛状态。在深度学习中，损失值有时
会在最终下降之前的多次迭代中保持不变或几乎保持不变，暂时形成收敛的假象。
另请参阅早停法 (#early_stopping)。
另请参阅 Boyd 和 Vandenberghe 合著的 Convex Optimization
(https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf)（《凸优化》）。

凸函数 (convex function)

一种函数，函数图像以上的区域为凸集 (#convex_set)。典型凸函数的形状类似于字母 U。
严格凸函数只有一个局部最低点，该点也是全局最低点。经典的 U 形函数都是严格凸函数。
不过，有些凸函数（例如直线）则不是这样。
很多常见的损失函数 (#loss_functions)（包括下列函数）都是凸函数：
L2 损失函数 (#L2_loss)
对数损失函数 (#Log_Loss)
L1 正则化 (#L1_regularization)
L2 正则化 (#L2_regularization)
梯度下降法 (#gradient_descent)的很多变体都一定能找到一个接近严格凸函数最小值的点。同
样，随机梯度下降法 (#SGD)的很多变体都有很高的可能性能够找到接近严格凸函数最小值的
点（但并非一定能找到）。
两个凸函数的和（例如 L2 损失函数 + L1 正则化）也是凸函数。
深度模型 (#deep_model)绝不会是凸函数。值得注意的是，专门针对凸优化
(#convex_optimization)设计的算法往往总能在深度网络上找到非常好的解决方案，虽然这些解
决方案并不一定对应于全局最小值。

凸优化 (convex optimization)

使用数学方法（例如梯度下降法 (#gradient_descent)）寻找凸函数 (#convex_function)最小值的
过程。机器学习方面的大量研究都是专注于如何通过公式将各种问题表示成凸优化问题，以及如何更高效地解决这些问题。
如需完整的详细信息，请参阅 Boyd 和 Vandenberghe 合著的 Convex Optimization
(https://web.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf)（《凸优化》）。

卷积 (convolution)

简单来说，卷积在数学中指两个函数的组合。在机器学习中，卷积结合使用卷积过滤器和输
入矩阵来训练权重。
机器学习中的“卷积”一词通常是卷积运算 (#convolutional_operation)或卷积层
(#convolutional_layer)的简称。
如果没有卷积，机器学习算法就需要学习大张量中每个单元格各自的权重。例如，用 2K x
2K 图像训练的机器学习算法将被迫找出 400 万个单独的权重。而使用卷积，机器学习算法
只需在卷积过滤器 (#convolutional_¦lter)中找出每个单元格的权重，大大减少了训练模型所需
的内存。在应用卷积过滤器后，它只需跨单元格进行复制，每个单元格都会与过滤器相乘。

卷积过滤器 (convolutional ‹lter)

卷积运算 (#convolutional_operation)中的两个参与方之一。（另一个参与方是输入矩阵切
片。）卷积过滤器是一种矩阵，其等级 (#rank)与输入矩阵相同，但形状小一些。以 28×28 的
输入矩阵为例，过滤器可以是小于 28×28 的任何二维矩阵。
在图形操作中，卷积过滤器中的所有单元格通常按照固定模式设置为 1 和 0。在机器学习
中，卷积过滤器通常先选择随机数字，然后由网络训练出理想值。

卷积层 (convolutional layer)

深度神经网络的一个层，卷积过滤器 (#convolutional_¦lter)会在其中传递输入矩阵。以下面的
3x3 卷积过滤器 (#convolutional_¦lter)为例：

下面的动画显示了一个由 9 个卷积运算（涉及 5x5 输入矩阵）组成的卷积层。请注意，每个
卷积运算都涉及一个不同的 3x3 输入矩阵切片。由此产生的 3×3 矩阵（右侧）就包含 9 个卷
积运算的结果：

积神经网络 (convolutional neural network)
一种神经网络，其中至少有一层为卷积层 (#convolutional_layer)。典型的卷积神经网络包含以
下几层的组合：

• 卷积层
• 池化层
• 密集层
  卷积神经网络在解决某些类型的问题（如图像识别）上取得了巨大成功。

卷积运算 (convolutional operation)

如下所示的两步数学运算：

1. 对卷积过滤器 (#convolutional_¦lter)和输入矩阵切片执行元素级乘法。（输入矩阵切片与
   卷积过滤器具有相同的等级和大小。）
2. 对生成的积矩阵中的所有值求和。
   以下面的 5x5 输入矩阵为例：

现在，以下面这个 2x2 卷积过滤器为例：

每个卷积运算都涉及一个 2x2 输入矩阵切片。例如，假设我们使用输入矩阵左上角的 2x2 切
片。这样一来，对此切片进行卷积运算将如下所示：

卷积层 (#convolutional_layer)由一系列卷积运算组成，每个卷积运算都针对不同的输入矩阵切
片。
成本 (cost)
与损失 (#loss)的含义相同。

交叉熵 (cross-entropy)

对数损失函数 (#Log_Loss)向多类别分类问题 (#multi-class)的一种泛化。交叉熵可以量化两种
概率分布之间的差异。另请参阅困惑度 (#perplexity)。

自定义 Estimator (custom Estimator)

您按照这些说明 (https://www.tensor§ow.org/extend/estimators)自行编写的 Estimator
(#Estimators)。 与预创建的 Estimator (#pre-made_Estimator) 相对。

D

数据分析 (data analysis)

根据样本、测量结果和可视化内容来理解数据。数据分析在首次收到数据集、构建第一个模
型之前特别有用。此外，数据分析在理解实验和调试系统问题方面也至关重要。

DataFrame

一种热门的数据类型，用于表示 Pandas 中的数据集。DataFrame 类似于表格。DataFrame
的每一列都有一个名称（标题），每一行都由一个数字标识。

数据集 (data set)

一组样本 (#example)的集合。

Dataset API (“.data)

一种高级别的 TensorFlow API，用于读取数据并将其转换为机器学习算法所需的格式。
tf.data.Dataset 对象表示一系列元素，其中每个元素都包含一个或多个张量 (#tensor)。 tf.data.Iterator 对象可获取 Dataset 中的元素。
如需详细了解 Dataset API，请参阅《TensorFlow 编程人员指南》中的导入数据
(https://www.tensor§ow.org/programmers_guide/datasets)。

决策边界 (decision boundary)

在二元分类 (#binary_classi¦cation)或多类别分类问题 (#multi-class)中，模型学到的类别之间的
分界线。例如，在以下表示某个二元分类问题的图片中，决策边界是橙色类别和蓝色类别之
间的分界线：

密集层 (dense layer)

与全连接层 (#fully_connected_layer)的含义相同。

深度模型 (deep model)

一种神经网络 (#neural_network)，其中包含多个隐藏层 (#hidden_layer)。深度模型依赖于可训练
的非线性关系。
与宽度模型 (#wide_model)相对。

密集特征 (dense feature)

一种大部分值是非零值的特征 (#feature)，通常是浮点值张量 (#tensor)。与稀疏特征
(#sparse_features)相对。

设备 (device)

一类可运行 TensorFlow 会话的硬件，包括 CPU、GPU 和 TPU。

离散特征 (discrete feature)

一种特征 (#feature)，包含有限个可能值。例如，某个值只能是“动物”、“蔬菜”或“矿物”的特征
便是一个离散特征（或分类特征）。与连续特征 (#continuous_feature)相对。

丢弃正则化 (dropout regularization)

正则化 (#regularization)的一种形式，在训练神经网络 (#neural_network)方面非常有用。丢弃正
则化的运作机制是，在一个梯度步长中移除从神经网络层中随机选择的固定数量的单元。丢
弃的单元越多，正则化效果就越强。这类似于训练神经网络以模拟较小网络的指数级规模集
成学习。如需完整的详细信息，请参阅 Dropout: A Simple Way to Prevent Neural Networks
from Over¦tting (http://jmlr.org/papers/volume15/srivastava14a.old/srivastava14a.pdf)（《丢弃：
一种防止神经网络过拟合的简单方法》）。

动态模型 (dynamic model)

一种模型 (#model)，以持续更新的方式在线接受训练。也就是说，数据会源源不断地进入这
种模型。

E

早停法 (early stopping)

一种正则化 (#regularization)方法，是指在训练损失仍可以继续降低之前结束模型训练。使用
早停法时，您会在验证数据集 (#validation_set)的损失开始增大（也就是泛化 (#generalization)效
果变差）时结束模型训练。

嵌套 (embeddings)

一种分类特征，以连续值特征表示。通常，嵌套是指将高维度向量映射到低维度的空间。例
如，您可以采用以下两种方式之一来表示英文句子中的单词：
表示成包含百万个元素（高维度）的稀疏向量 (#sparse_features)，其中所有元素都是整
数。向量中的每个单元格都表示一个单独的英文单词，单元格中的值表示相应单词在句
子中出现的次数。由于单个英文句子包含的单词不太可能超过 50 个，因此向量中几乎
每个单元格都包含 0。少数非 0 的单元格中将包含一个非常小的整数（通常为 1），该
整数表示相应单词在句子中出现的次数。
表示成包含数百个元素（低维度）的密集向量 (#dense_feature)，其中每个元素都存储一
个介于 0 到 1 之间的浮点值。这就是一种嵌套。
在 TensorFlow 中，会按反向传播 (#backpropagation)损失 (#loss)训练嵌套，和训练神经网络
(#neural_network)中的任何其他参数一样。

经验风险最小化 (ERM, empirical risk minimization)

用于选择可以将基于训练集的损失降至最低的函数。与结构风险最小化 (#SRM)相对。

集成学习 (ensemble)

多个模型 (#model)的预测结果的并集。您可以通过以下一项或多项来创建集成学习：
不同的初始化
不同的超参数 (#hyperparameter)
不同的整体结构
深度模型和宽度模型 (https://www.tensor§ow.org/tutorials/wide_and_deep)属于一种集成学习。

周期 (epoch)

在训练时，整个数据集的一次完整遍历，以便不漏掉任何一个样本。因此，一个周期表示
（N/批次大小 (#batch_size)）次训练迭代 (#iteration)，其中 N 是样本总数。

Estimator

tf.Estimator 类的一个实例，用于封装负责构建 TensorFlow 图并运行 TensorFlow 会话的
逻辑。您可以创建自定义 Estimator (#custom_estimator)（如需相关介绍，请点击此处
(https://www.tensor§ow.org/extend/estimators)），也可以实例化其他人预创建的 Estimator
(#pre-made_Estimator)。

样本 (example)

数据集的一行。一个样本包含一个或多个特征 (#feature)，此外还可能包含一个标签 (#label)。
另请参阅有标签样本 (#labeled_example)和无标签样本 (#unlabeled_example)。

F

假负例 (FN, false negative)
被模型错误地预测为负类别 (#negative_class)的样本。例如，模型推断出某封电子邮件不是垃
圾邮件（负类别），但该电子邮件其实是垃圾邮件。
假正例 (FP, false positive)
被模型错误地预测为正类别 (#positive_class)的样本。例如，模型推断出某封电子邮件是垃圾
邮件（正类别），但该电子邮件其实不是垃圾邮件。
假正例率（false positive rate, 简称 FP 率）
ROC 曲线 (#ROC)中的 x 轴。FP 率的定义如下：

特征 (feature)

在进行预测 (#prediction)时使用的输入变量。

特征列 (“.feature_column)

指定模型应该如何解读特定特征的一种函数。此类函数的输出结果是所有 Estimators
(#Estimators) 构造函数的必需参数。
借助 tf.feature_column 函数，模型可对输入特征的不同表示法轻松进行实验。有关详
情，请参阅《TensorFlow 编程人员指南》中的特征列
(https://www.tensor§ow.org/get_started/feature_columns)一章。
“特征列”是 Google 专用的术语。特征列在 Yahoo/Microsoft 使用的 VW
(https://en.wikipedia.org/wiki/Vowpal_Wabbit) 系统中称为“命名空间”，也称为场
(https://www.csie.ntu.edu.tw/~cjlin/libffm/)。

特征组合 (feature cross)

通过将单独的特征进行组合（求笛卡尔积）而形成的合成特征 (#synthetic_feature)。特征组合
有助于表达非线性关系。

特征工程 (feature engineering)

指以下过程：确定哪些特征 (#feature)可能在训练模型方面非常有用，然后将日志文件及其他
来源的原始数据转换为所需的特征。在 TensorFlow 中，特征工程通常是指将原始日志文件
条目转换为 tf.Example (#tf.Example) 协议缓冲区。另请参阅 tf.Transform
(https://github.com/tensor§ow/transform)。
特征工程有时称为特征提取。

特征集 (feature set)

训练机器学习模型时采用的一组特征 (#feature)。例如，对于某个用于预测房价的模型，邮政
编码、房屋面积以及房屋状况可以组成一个简单的特征集。

特征规范 (feature spec)

用于描述如何从 tf.Example (#tf.Example) 协议缓冲区提取特征 (#feature)数据。由于
tf.Example 协议缓冲区只是一个数据容器，因此您必须指定以下内容：
要提取的数据（即特征的键）
数据类型（例如 §oat 或 int）
长度（固定或可变）
Estimator API (#Estimators) 提供了一些可用来根据给定 FeatureColumns (#feature_columns)
列表生成特征规范的工具。

少量样本学习 (few-shot learning)

一种机器学习方法（通常用于对象分类），旨在仅通过少量训练样本学习有效的分类器。

全连接层 (fully connected layer)

一种隐藏层 (#hidden_layer)，其中的每个节点 (#node)均与下一个隐藏层中的每个节点相连。
全连接层又称为密集层 (#dense_layer)。

G

泛化 (generalization)
指的是模型依据训练时采用的数据，针对以前未见过的新数据做出正确预测的能力。
广义线性模型 (generalized linear model)
最小二乘回归 (#least_squares_regression)模型（基于高斯噪声
(https://en.wikipedia.org/wiki/Gaussian_noise)）向其他类型的模型（基于其他类型的噪声，例如
泊松噪声 (https://en.wikipedia.org/wiki/Shot_noise)或分类噪声）进行的一种泛化。广义线性模型
的示例包括：

• 逻辑回归 (#logistic_regression)
• 多类别回归
• 最小二乘回归

可以通过凸优化 (https://en.wikipedia.org/wiki/Convex_optimization)找到广义线性模型的参数。
广义线性模型具有以下特性：

• 最优的最小二乘回归模型的平均预测结果等于训练数据的平均标签。
• 最优的逻辑回归模型预测的平均概率等于训练数据的平均标签。

广义线性模型的功能受其特征的限制。与深度模型不同，广义线性模型无法“学习新特征”。
梯度 (gradient)
偏导数 (#partial_derivative)相对于所有自变量的向量。在机器学习中，梯度是模型函数偏导数
的向量。梯度指向最高速上升的方向。
梯度裁剪 (gradient clipping)
在应用梯度 (#gradient)值之前先设置其上限。梯度裁剪有助于确保数值稳定性以及防止梯度爆
炸
(http://www.cs.toronto.edu/~rgrosse/courses/csc321_2017/readings/L15%20Exploding%20and%20Va
nishing%20Gradients.pdf) 。

梯度下降法 (gradient descent)

一种通过计算并且减小梯度将损失 (#loss)降至最低的技术，它以训练数据为条件，来计算损
失相对于模型参数的梯度。通俗来说，梯度下降法以迭代方式调整参数，逐渐找到权重
(#weight)和偏差的最佳组合，从而将损失降至最低。

图 (graph)

TensorFlow 中的一种计算规范。图中的节点表示操作。边缘具有方向，表示将某项操作的结
果（一个张量 (https://www.tensor§ow.org/api_docs/python/tf/Tensor)）作为一个操作数传递给另
一项操作。可以使用 TensorBoard (#TensorBoard) 直观呈现图。

H

启发法 (heuristic)

一种非最优但实用的问题解决方案，足以用于进行改进或从中学习。

隐藏层 (hidden layer)

神经网络 (#neural_network)中的合成层，介于输入层 (#input_layer)（即特征）和输出层
(#output_layer)（即预测）之间。神经网络包含一个或多个隐藏层。

合页损失函数 (hinge loss)

一系列用于分类 (#classi¦cation_model)的损失 (#loss)函数，旨在找到距离每个训练样本都尽可
能远的决策边界 (#decision_boundary)，从而使样本和边界之间的裕度最大化。 KSVM
(#KSVMs) 使用合页损失函数（或相关函数，例如平方合页损失函数）。对于二元分类，合页
损失函数的定义如下：

其中“y’”表示分类器模型的原始输出：

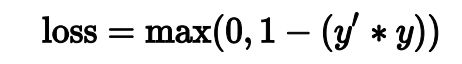
“y”表示真标签，值为 -1 或 +1。
因此，合页损失与 (y * y’) 的关系图如下所示：

维持数据 (holdout data)

训练期间故意不使用（“维持”）的样本 (#example)。验证数据集 (#validation_set)和测试数据集
(#test_set)都属于维持数据。维持数据有助于评估模型向训练时所用数据之外的数据进行泛化
的能力。与基于训练数据集的损失相比，基于维持数据集的损失有助于更好地估算基于未见
过的数据集的损失。

超参数 (hyperparameter)

在模型训练的连续过程中，您调节的“旋钮”。例如，学习速率 (#learning_rate)就是一种超参
数。
与参数 (#parameter)相对。

超平面 (hyperplane)

将一个空间划分为两个子空间的边界。例如，在二维空间中，直线就是一个超平面，在三维
空间中，平面则是一个超平面。在机器学习中更典型的是：超平面是分隔高维度空间的边
界。核支持向量机 (#KSVMs)利用超平面将正类别和负类别区分开来（通常是在极高维度空间
中）。
I

独立同等分布 (i.i.d, independently and identically distributed)

从不会改变的分布中提取的数据，其中提取的每个值都不依赖于之前提取的值。i.i.d. 是机器
学习的理想气体 (https://en.wikipedia.org/wiki/Ideal_gas) - 一种实用的数学结构，但在现实世界
中几乎从未发现过。例如，某个网页的访问者在短时间内的分布可能为 i.i.d.，即分布在该短
时间内没有变化，且一位用户的访问行为通常与另一位用户的访问行为无关。不过，如果将
时间窗口扩大，网页访问者的分布可能呈现出季节性变化。

推断 (inference)

在机器学习中，推断通常指以下过程：通过将训练过的模型应用于无标签样本
(#unlabeled_example)来做出预测。在统计学中，推断是指在某些观测数据条件下拟合分布参
数的过程。（请参阅维基百科中有关统计学推断的文章
(https://en.wikipedia.org/wiki/Statistical_inference)。）

输入函数 (input function)

在 TensorFlow 中，用于将输入数据返回到 Estimator (#Estimators) 的训练、评估或预测方法
的函数。例如，训练输入函数会返回训练集 (#training_set)中的一批 (#batch)特征和标签。

输入层 (input layer)

神经网络 (#neural_network)中的第一层（接收输入数据的层）。

实例 (instance)

与样本 (#example)的含义相同。

可解释性 (interpretability)

模型的预测可解释的难易程度。深度模型通常不可解释，也就是说，很难对深度模型的不同
层进行解释。相比之下，线性回归模型和宽度模型 (#wide_model)的可解释性通常要好得多。

评分者间一致性信度 (inter-rater agreement)

一种衡量指标，用于衡量在执行某项任务时评分者达成一致的频率。如果评分者未达成一
致，则可能需要改进任务说明。有时也称为注释者间一致性信度或评分者间可靠性信度。另
请参阅 Cohen’s kappa (https://en.wikipedia.org/wiki/Cohen%27s_kappa)（最热门的评分者间一致
性信度衡量指标之一）。

迭代 (iteration)

模型的权重在训练期间的一次更新。迭代包含计算参数在单批次 (#batch)数据上的梯度损失。

K

k-means
一种热门的聚类 (#clustering)算法，用于对非监督式学习中的样本进行分组。k-means 算法基
本上会执行以下操作：
以迭代方式确定最佳的 k 中心点（称为形心 (#centroid)）。
将每个样本分配到最近的形心。与同一个形心距离最近的样本属于同一个组。
k-means 算法会挑选形心位置，以最大限度地减小每个样本与其最接近形心之间的距离的累
积平方。
以下面的小狗高度与小狗宽度的关系图为例：

如果 k=3，则 k-means 算法会确定三个形心。每个样本都被分配到与其最接近的形心，最终
产生三个组：

假设制造商想要确定小、中和大号狗毛衣的理想尺寸。在该聚类中，三个形心用于标识每只
狗的平均高度和平均宽度。因此，制造商可能应该根据这三个形心确定毛衣尺寸。请注意，
聚类的形心通常不是聚类中的样本。
上图显示了 k-means 应用于仅具有两个特征（高度和宽度）的样本。请注意，k-means 可以
跨多个特征为样本分组。
k-median 与 k-means (#k-means) 紧密相关的聚类算法。两者的实际区别如下：
对于 k-means，确定形心的方法是，最大限度地减小候选形心与它的每个样本之间的距
离平方和。
对于 k-median，确定形心的方法是，最大限度地减小候选形心与它的每个样本之间的
距离总和。
请注意，距离的定义也有所不同：

• k-means 采用从形心到样本的欧几里得距离
  (https://en.wikipedia.org/wiki/Euclidean_distance)。（在二维空间中，欧几里得距离即使用
  勾股定理来计算斜边。）例如，(2,2) 与 (5,-2) 之间的 k-means 距离为：
  

• k-median 采用从形心到样本的曼哈顿距离 (https://en.wikipedia.org/wiki/Taxicab_geometry)
  。这个距离是每个维度中绝对差异值的总和。例如，(2,2) 与 (5,-2) 之间的 k-median 距
  离为：
  

Keras

一种热门的 Python 机器学习 API。Keras (https://keras.io) 能够在多种深度学习框架上运行，
其中包括 TensorFlow（在该框架上，Keras 作为 tf.keras
(https://www.tensor§ow.org/api_docs/python/tf/keras) 提供）。

核支持向量机 (KSVM, Kernel Suppo’ Vector Machines)

一种分类算法，旨在通过将输入数据向量映射到更高维度的空间，来最大化正类别
(#positive_class)和负类别 (#negative_class)之间的裕度。以某个输入数据集包含一百个特征的
分类问题为例。为了最大化正类别和负类别之间的裕度，KSVM 可以在内部将这些特征映射
到百万维度的空间。KSVM 使用合页损失函数 (#hinge-loss)。

L

L1 损失函数 (L₁ loss)

一种损失 (#loss)函数，基于模型预测的值与标签 (#label)的实际值之差的绝对值。与 L2 损失
函数 (#squared_loss)相比，L1 损失函数对离群值的敏感性弱一些。

L1 正则化 (L₁ regularization)

一种正则化 (#regularization)，根据权重的绝对值的总和来惩罚权重。在依赖稀疏特征
(#sparse_features)的模型中，L1 正则化有助于使不相关或几乎不相关的特征的权重正好为
0，从而将这些特征从模型中移除。与 L2 正则化 (#L2_regularization)相对。

L2 损失函数 (L₂ loss)

请参阅平方损失函数 (#squared_loss)。 L2 正则化 (L₂ regularization)
一种正则化 (#regularization)，根据权重的平方和来惩罚权重。L2 正则化有助于使离群值（具
有较大正值或较小负值）权重接近于 0，但又不正好为 0。（与 L1 正则化 (#L1_regularization)
相对。）在线性模型中，L2 正则化始终可以改进泛化。

标签 (label)

在监督式学习中，标签指样本 (#example)的“答案”或“结果”部分。有标签数据集中的每个样本
都包含一个或多个特征以及一个标签。例如，在房屋数据集中，特征可能包括卧室数、卫生
间数以及房龄，而标签则可能是房价。在垃圾邮件检测数据集中，特征可能包括主题行、发
件人以及电子邮件本身，而标签则可能是“垃圾邮件”或“非垃圾邮件”。

有标签样本 (labeled example)

包含特征 (#feature)和标签 (#label)的样本。在监督式训练中，模型从有标签样本中学习规律。

lambda

与正则化率 (#regularization_rate)的含义相同。
（多含义术语，我们在此关注的是该术语在正则化 (#regularization)中的定义。）

层 (layer)

神经网络 (#neural_network)中的一组神经元 (#neuron)，负责处理一组输入特征，或一组神经元
的输出。
此外还指 TensorFlow 中的抽象层。层是 Python 函数，以张量 (#tensor)和配置选项作为输
入，然后生成其他张量作为输出。当必要的张量组合起来后，用户便可以通过模型函数
(#model_function)将结果转换为 Estimator (#Estimators)。

Layers API (“.layers)

一种 TensorFlow API，用于以层组合的方式构建深度 (#deep_model)神经网络。通过 Layers
API，您可以构建不同类型的层 (#layer)，例如：
通过 tf.layers.Dense 构建全连接层 (#fully_connected_layer)。
通过 tf.layers.Conv2D 构建卷积层。
在编写自定义 Estimator (#custom_estimator) 时，您可以编写“层”对象来定义所有隐藏层
(#hidden_layers)的特征。
Layers API 遵循 Keras (#Keras) layers API 规范。也就是说，除了前缀不同以外，Layers API
中的所有函数均与 Keras layers API 中的对应函数具有相同的名称和签名。

学习速率 (learning rate)

在训练模型时用于梯度下降的一个标量。在每次迭代期间，梯度下降法 (#gradient_descent)都
会将学习速率与梯度相乘。得出的乘积称为梯度步长。
学习速率是一个重要的超参数 (#hyperparameter)。

最小二乘回归 (least squares regression)

一种通过最小化 L2 损失 (#L2_loss)训练出的线性回归模型。

线性回归 (linear regression)

一种回归模型 (#regression_model)，通过将输入特征进行线性组合输出连续值。

逻辑回归 (logistic regression)

一种模型，通过将 S 型函数 (#sigmoid_function)应用于线性预测，生成分类问题中每个可能的
离散标签值的概率。虽然逻辑回归经常用于二元分类 (#binary_classi¦cation)问题，但也可用于
多类别 (#multi-class)分类问题（其叫法变为多类别逻辑回归或多项回归）。

对数 (logits)

分类模型生成的原始（非标准化）预测向量，通常会传递给标准化函数。如果模型要解决多
类别分类问题，则对数通常变成 softmax 函数
(https://www.tensor§ow.org/api_docs/python/tf/nn/softmax_cross_entropy_with_logits_v2)的输入。
之后，softmax 函数会生成一个（标准化）概率向量，对应于每个可能的类别。
此外，对数有时也称为 S 型函数 (#sigmoid_function)的元素级反函数。如需了解详细信息，请
参阅 tf.nn.sigmoid_cross_entropy_with_logits

对数损失函数 (Log Loss)

二元逻辑回归 (#logistic_regression)中使用的损失 (#loss)函数。

对数几率 (log-odds)

某个事件几率的对数。
如果事件涉及二元概率，则几率指的是成功概率 § 与失败概率 (1-p) 之比。例如，假设某个
给定事件的成功概率为 90％，失败概率为 10％。在这种情况下，几率的计算公式如下：

简单来说，对数几率即几率的对数。按照惯例，“对数”指自然对数，但对数的基数其实可以
是任何大于 1 的数。若遵循惯例，上述示例的对数几率应为：

对数几率是 S 型函数 (#sigmoid_function)的反函数.

损失 (Loss)

一种衡量指标，用于衡量模型的预测 (#prediction)偏离其标签 (#label)的程度。或者更悲观地说
是衡量模型有多差。要确定此值，模型必须定义损失函数。例如，线性回归模型通常将均方
误差 (#MSE)用作损失函数，而逻辑回归模型则使用对数损失函数 (#Log_Loss)。

M

机器学习 (machine learning)

一种程序或系统，用于根据输入数据构建（训练）预测模型。这种系统会利用学到的模型根
据从分布（训练该模型时使用的同一分布）中提取的新数据（以前从未见过的数据）进行实
用的预测。机器学习还指与这些程序或系统相关的研究领域。

均方误差 (MSE, Mean Squared Error)

每个样本的平均平方损失。MSE 的计算方法是平方损失 (#squared_loss)除以样本 (#example)
数。TensorFlow Playground (#TensorFlow_Playground) 显示的“训练损失”值和“测试损失”值都
是 MSE。

指标 (metric)

您关心的一个数值。可能可以也可能不可以直接在机器学习系统中得到优化。您的系统尝试
优化的指标称为目标 (#objective)。 Metrics API (“.metrics)
一种用于评估模型的 TensorFlow API。例如，tf.metrics.accuracy 用于确定模型的预测
与标签匹配的频率。在编写自定义 Estimator (#custom_estimator) 时，您可以调用 Metrics
API 函数来指定应如何评估您的模型。

小批次 (mini-batch)

从整批样本 (#example)内随机选择并在训练或推断过程的一次迭代中一起运行的一小部分样
本。小批次的批次大小 (#batch_size)通常介于 10 到 1000 之间。与基于完整的训练数据计算
损失相比，基于小批次数据计算损失要高效得多。
小批次随机梯度下降法 (SGD, mini-batch stochastic gradient descent)
一种采用小批次 (#mini-batch)样本的梯度下降法 (#gradient_descent)。也就是说，小批次 SGD
会根据一小部分训练数据来估算梯度。Vanilla SGD (#SGD) 使用的小批次的大小为 1。

模型 (model)

机器学习系统从训练数据学到的内容的表示形式。多含义术语，可以理解为下列两种相关含
义之一：

• 一种 TensorFlow (#TensorFlow) 图，用于表示预测的计算结构。
• 该 TensorFlow 图的特定权重和偏差，通过训练 (#model_training)决定。

模型函数 (model function)

Estimator (#Estimators) 中的函数，用于实现机器学习训练、评估和推断。例如，模型函数的
训练部分可以处理以下任务：定义深度神经网络的拓扑并确定其优化器 (#optimizer)函数。如
果使用预创建的 Estimator (#pre-made_Estimator)，则有人已为您编写了模型函数。如果使用
自定义 Estimator (#custom_estimator)，则必须自行编写模型函数。
有关编写模型函数的详细信息，请参阅创建自定义 Estimator
(https://www.tensor§ow.org/get_started/custom_estimators)。

模型训练 (model training)

确定最佳模型 (#model)的过程。

动量 (Momentum)

一种先进的梯度下降法，其中学习步长不仅取决于当前步长的导数，还取决于之前一步或多
步的步长的导数。动量涉及计算梯度随时间而变化的指数级加权移动平均值，与物理学中的
动量类似。动量有时可以防止学习过程被卡在局部最小的情况。

多类别分类 (multi-class classi‹cation)

区分两种以上类别的分类问题。例如，枫树大约有 128 种，因此，确定枫树种类的模型就属
于多类别模型。反之，仅将电子邮件分为两类（“垃圾邮件”和“非垃圾邮件”）的模型属于二元

分类模型 (#binary_classi¦cation)。

多项分类 (multinomial classi‹cation) 与多类别分类 (#multi-class)的含义相同。

N

NaN 陷阱 (NaN trap)

模型中的一个数字在训练期间变成 NaN (https://en.wikipedia.org/wiki/NaN)，这会导致模型中的
很多或所有其他数字最终也会变成 NaN。
NaN 是“非数字”的缩写。

负类别 (negative class)

在二元分类 (#binary_classi¦cation)中，一种类别称为正类别，另一种类别称为负类别。正类别
是我们要寻找的类别，负类别则是另一种可能性。例如，在医学检查中，负类别可以是“非肿
瘤”。在电子邮件分类器中，负类别可以是“非垃圾邮件”。另请参阅正类别 (#positive_class)。

神经网络 (neural network)

一种模型，灵感来源于脑部结构，由多个层构成（至少有一个是隐藏层 (#hidden_layer)），每
个层都包含简单相连的单元或神经元 (#neuron)（具有非线性关系）。

神经元 (neuron)

神经网络 (#neural_network)中的节点，通常会接收多个输入值并生成一个输出值。神经元通过
将激活函数 (#activation_function)（非线性转换）应用于输入值的加权和来计算输出值。

节点 (node)

多含义术语，可以理解为下列两种含义之一：
隐藏层 (#hidden_layer)中的神经元。
TensorFlow 图 (#graph)中的操作。

标准化 (normalization)

将实际的值区间转换为标准的值区间（通常为 -1 到 +1 或 0 到 1）的过程。例如，假设某个
特征的自然区间是 800 到 6000。通过减法和除法运算，您可以将这些值标准化为位于 -1 到
+1 区间内。
另请参阅缩放 (#scaling)。

数值数据 (numerical data)

用整数或实数表示的特征 (#feature)。例如，在房地产模型中，您可能会用数值数据表示房子
大小（以平方英尺或平方米为单位）。如果用数值数据表示特征，则可以表明特征的值相互
之间具有数学关系，并且与标签可能也有数学关系。例如，如果用数值数据表示房子大小，
则可以表明面积为 200 平方米的房子是面积为 100 平方米的房子的两倍。此外，房子面积的
平方米数可能与房价存在一定的数学关系。
并非所有整数数据都应表示成数值数据。例如，世界上某些地区的邮政编码是整数，但在模
型中，不应将整数邮政编码表示成数值数据。这是因为邮政编码 20000 在效力上并不是邮政
编码 10000 的两倍（或一半）。此外，虽然不同的邮政编码确实与不同的房地产价值有关，
但我们也不能假设邮政编码为 20000 的房地产在价值上是邮政编码为 10000 的房地产的两
倍。邮政编码应表示成分类数据 (#categorical_data)。
数值特征有时称为连续特征 (#continuous_feature)。

目标 (objective)

算法尝试优化的指标。

离线推断 (oˆine inference)

生成一组预测 (#prediction)，存储这些预测，然后根据需求检索这些预测。与在线推断
(#online_inference)相对。

独热编码 (one-hot encoding)

一种稀疏向量，其中：
一个元素设为 1。
所有其他元素均设为 0。
独热编码常用于表示拥有有限个可能值的字符串或标识符。例如，假设某个指定的植物学数
据集记录了 15000 个不同的物种，其中每个物种都用独一无二的字符串标识符来表示。在特
征工程过程中，您可能需要将这些字符串标识符编码为独热向量，向量的大小为 15000。

单样本学习（one-shot learning，通常用于对象分类）

一种机器学习方法，通常用于对象分类，旨在通过单个训练样本学习有效的分类器。
另请参阅少量样本学习 (#few-shot_learning)。

一对多 (one-vs.-all)

假设某个分类问题有 N 种可能的解决方案，一对多解决方案将包含 N 个单独的二元分类器
(#binary_classi¦cation) - 一个二元分类器对应一种可能的结果。例如，假设某个模型用于区分
样本属于动物、蔬菜还是矿物，一对多解决方案将提供下列三个单独的二元分类器：
动物和非动物
蔬菜和非蔬菜
矿物和非矿物

在线推断 (online inference)

根据需求生成预测 (#prediction)。与离线推断 (#o©ine_inference)相对。

操作 (op, Operation)

TensorFlow 图中的节点。在 TensorFlow 中，任何创建、操纵或销毁张量 (#tensor)的过程都
属于操作。例如，矩阵相乘就是一种操作，该操作以两个张量作为输入，并生成一个张量作
为输出。

优化器 (optimizer)

梯度下降法 (#gradient_descent)的一种具体实现。TensorFlow 的优化器基类是
tf.train.Optimizer (https://www.tensor§ow.org/api_docs/python/tf/train/Optimizer)。不同的优化器
可能会利用以下一个或多个概念来增强梯度下降法在指定训练集 (#training_set)中的效果：
动量 (https://www.tensor§ow.org/api_docs/python/tf/train/MomentumOptimizer) (Momentum)
更新频率（AdaGrad (https://www.tensor§ow.org/api_docs/python/tf/train/AdagradOptimizer)
= ADAptive GRADient descent；Adam
(https://www.tensor§ow.org/api_docs/python/tf/train/AdamOptimizer) = ADAptive with
Momentum；RMSProp）
稀疏性/正则化 (Ftrl (https://www.tensor§ow.org/api_docs/python/tf/train/FtrlOptimizer))
更复杂的数学方法（Proximal
(https://www.tensor§ow.org/api_docs/python/tf/train/ProximalGradientDescentOptimizer)，等
等）
甚至还包括 NN 驱动的优化器 (https://arxiv.org/abs/1606.04474)。

离群值 (outlier)

与大多数其他值差别很大的值。在机器学习中，下列所有值都是离群值。
绝对值很高的权重 (#weight)。
与实际值相差很大的预测值。
值比平均值高大约 3 个标准偏差的输入数据。
离群值常常会导致模型训练出现问题。

输出层 (output layer)

神经网络的“最后”一层，也是包含答案的层。

过拟合 (ovei”ing)

创建的模型与训练数据 (#training_set)过于匹配，以致于模型无法根据新数据做出正确的预
测。

参数 (parameter)

机器学习系统自行训练的模型的变量。例如，权重 (#weight)就是一种参数，它们的值是机器
学习系统通过连续的训练迭代逐渐学习到的。与超参数 (#hyperparameter)相对。
参数服务器 (PS, Parameter Server)
一种作业，负责在分布式设置中跟踪模型参数 (#parameter)。

参数更新 (parameter update)

在训练期间（通常是在梯度下降法 (#gradient_descent)的单次迭代中）调整模型参数
(#parameter)的操作。

偏导数 (pa’ial derivative)

一种导数，除一个变量之外的所有变量都被视为常量。例如，f(x, y) 对 x 的偏导数就是 f(x)
的导数（即，使 y 保持恒定）。f 对 x 的偏导数仅关注 x 如何变化，而忽略公式中的所有其他
变量。

划分策略 (pa’itioning strategy)

在参数服务器 (#Parameter_Server)间分割变量的算法。

性能 (peormance)

多含义术语，具有以下含义：
在软件工程中的传统含义。即：相应软件的运行速度有多快（或有多高效）？
在机器学习中的含义。在机器学习领域，性能旨在回答以下问题：相应模型 (#model)的
准确度有多高？即模型在预测方面的表现有多好？

困惑度 (perplexity)

一种衡量指标，用于衡量模型 (#model)能够多好地完成任务。例如，假设任务是读取用户使
用智能手机键盘输入字词时输入的前几个字母，然后列出一组可能的完整字词。此任务的困
惑度 § 是：为了使列出的字词中包含用户尝试输入的实际字词，您需要提供的猜测项的个
数。
困惑度与交叉熵 (#cross-entropy)的关系如下：

流水线 (pipeline)

机器学习算法的基础架构。流水线包括收集数据、将数据放入训练数据文件、训练一个或多
个模型，以及将模型导出到生产环境。

池化 (pooling)

将一个或多个由前趋的卷积层 (#convolutional_layer)创建的矩阵压缩为较小的矩阵。池化通常
是取整个池化区域的最大值或平均值。以下面的 3x3 矩阵为例：
池化运算与卷积运算类似：将矩阵分割为多个切片，然后按步长 (#stride)逐个运行卷积运算。
例如，假设池化运算按 1x1 步长将卷积矩阵分割为 2x2 个切片。如下图所示，进行了四个池
化运算。假设每个池化运算都选择该切片中四个值的最大值：
池化有助于在输入矩阵中实现平移不变性 (#translational_invariance)。
对于视觉应用来说，池化的更正式名称为空间池化。时间序列应用通常将池化称为时序池
化。按照不太正式的说法，池化通常称为下采样或降采样。

正类别 (positive class)

在二元分类 (#binary_classi¦cation)中，两种可能的类别分别被标记为正类别和负类别。正类别
结果是我们要测试的对象。（不可否认的是，我们会同时测试这两种结果，但只关注正类别
结果。）例如，在医学检查中，正类别可以是“肿瘤”。在电子邮件分类器中，正类别可以
是“垃圾邮件”。 与负类别 (#negative_class)相对。

本术语表中列出了一般的机器学习术语和 TensorFlow 专用术语的定义。
以下内容可下载:https://download.csdn.net/download/bigdata_wangzhe/15543442