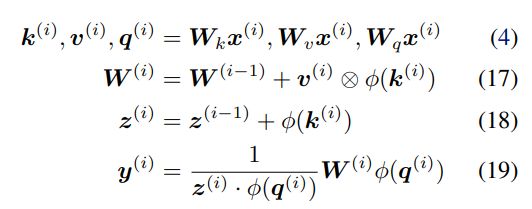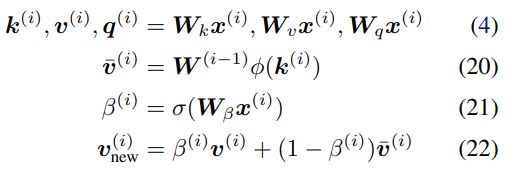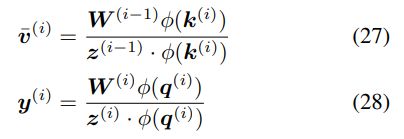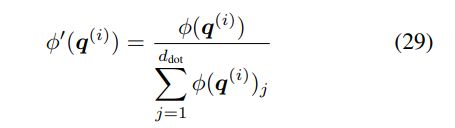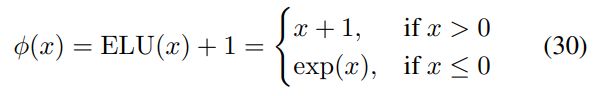LSTM之父重提30年前的「快速权重存储系统」：线性Transformer只是它的一种变体...

作者｜陈萍、维度

 来源｜机器之心

来自瑞士人工智能实验室、亚琛工业大学的研究者建立了线性（核）注意力与快速权重存储系统之间的内在联系，并提出更新规则，在合成检索问题、机器翻译、语言模型等实验上性能优越。

Transformer 在深度学习中占据主导地位，但二次存储和计算需求使得 Transformer 的训练成本很高，而且很难使用。许多研究都尝试线性化核心模块：以 Performer 为例，使用带核的注意力机制。然而，这种方法还存在很多缺点，例如它们依赖于随机特征。

本文中，来自瑞士人工智能实验室（IDSIA）、亚琛工业大学的研究者建立起了线性（核）注意力与 90 年代深度学习之父 Jürgen Schmidhuber 推广的更古老的快速权重存储系统之间的内在联系，不仅指出了这些算法的基本局限性，还提出了新的更新规则和新的核来解决这些问题。在关键的综合实验和实际任务中，所得到的模型优于 Performers。

论文链接：

https://arxiv.org/abs/2102.11174

代码地址：

https://github.com/ischlag/fast-weight-transformers

具体而言，该研究推测线性化的 softmax 注意力变量存在存储容量限制。在有限存储的情况下，快速权重存储模型的一个理想行为是操纵存储的内容并与之动态交互。

受过去对快速权重研究的启发，研究者建议用产生这种行为的替代规则替换更新规则。此外，该研究还提出了一个新的核函数来线性化注意力，平衡简单性和有效性。他们进行了大量的实验，实验内容包括合成检索问题、标准机器翻译以及语言建模。实验结果证明了该研究方法的益处。

将线性 Transformer 作为快速权重系统进行分析和改进

将线性 Transformer 变量视为快速权重系统，研究者给出了两个见解：作为关联存储容量的限制；无法编辑以前存储的关联内容。

容量限制

不断地将新的关联添加到有限大小的存储中，如下公式 17 所示，这样不可避免地会达到极限。在线性注意力中，信息存储在矩阵中，并使用矩阵乘法进行检索（如下公式 19）。因此，为了防止关联在检索时相互干扰，各个键（keys）需要正交。否则，点积将处理多个键并返回值的线性组合。对于嵌入在 d_dot 空间中的键，则不能有多余 d_dot 正交向量。

也就是说，存储多个 d_dot 关联将导致检索误差。在线性 Transformer 中，当序列长度大于 d_dot 时，模型可能处于这样一种容量过剩状态。

改进与更新

受快速权重存储研究（Schlag 等人，2021 年）的启发，研究者提出了以下存储更新规则。

给定新的输入键 - 值对 (k^ (i) , v ^(i) )，模型首先访问存储的当前状态 W^(i−1)，并检索当前与键 k^(i) 配对的值。然后，该模型存储检索值和输入 v^(i) 的凸组合，使用插值权重 0≤β^(i)≤1 的输入 v ^(i) 也由该模型生成。因此，该模型按顺序将输入序列转化为输出序列，如下所示：

归一化：在以上等式中，检索的值没有应用归一化。通过推导可以得到一个简单的归一化，即通过引入累加器（accumulator）：

将公式 20、25 分别替换为：

然而，这种方法也有缺陷。首先，公式 26 中正值的累积总是随着步数的增加而增加，并且可能导致不稳定；其次，特别是对于该研究提出的更新规则，这种归一化不足以平衡公式 23 中写入和删除运算之间的权重（参见附录 A.2 中的推导）。

在这里，研究者提出了一种基于简单归一化的更好方法，将有效值和查询向量φ(k^(i))、φ(q^(i)) 除以其分量之和。例如，对于查询：

线性注意力函数

Katharopoulos 线性注意力

Katharopoulos 等人提出使用简单的逐元素 ELU + 1 函数（Clevert 等人， 2016）：

选择 ELU 而不是 ReLU 的动机是因为负数部分的非零梯度。重要的是，作为一个简单的函数，这个Φ函数保留了输入键向量（d_key=d_dot）的维数，而不需要修改第 4.1 节中讨论的存储容量。

DPFP

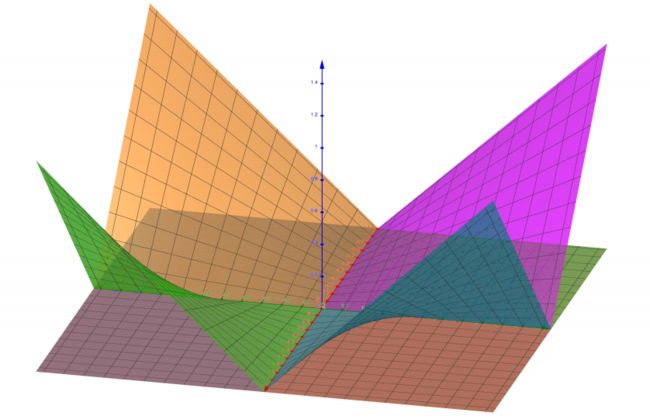
前面两小节强调了现有Φ函数的次优性。采样会给 FAVOR + 增加额外的复杂度，而线性 Transformer 缺乏投影点积维数的能力。因此，研究者提出了一种称为确定性无参数投影（deterministic parameter-free projection, DPFP） 的替代方法。它是确定性的，并像线性 Transformer 一样易于计算，同时增加点积维数，而不需要 FAVOR + 的随机特性。

下图中四维空间的元素被显示为四个彩色表面的 z 分量，以及 2d 平面中的每个向量如何在 4d 空间中具有单个非零分量，并将输入空间平均分割为在投影空间中正交的四个区域。

实验

该研究从三个方面进行了实验：合成检索问题、机器翻译和语言模型。

合成检索问题

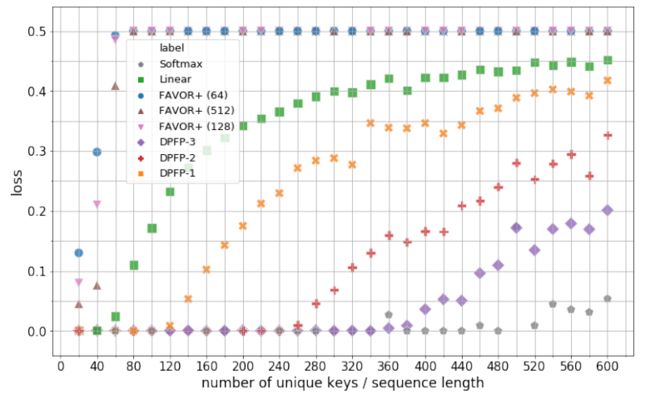
所有模型都以最小批次 32 进行训练，直到评估损失降到 0.001 以下，或者进行了 1000 训练步。下图 2 展示了模型的最佳验证集性能以及对不同 S 的显示。唯一键的数量初始值 S=20，然后每次递增 20，直到 S=600 为止。实验对以下模型进行对比：Softmax、线性注意力、具有 64、128 和 512 个随机特征的 FAVOR + 以及ν∈{1、2、3} 的 DPFP-ν。

下图 3 展示了学习曲线。实验结果表明，该研究提出的更新规则优于其他变体。正如预期的那样，基线总和更新规则失败。

机器翻译

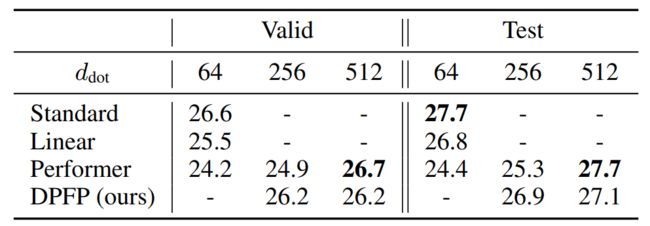
下表 1 显示了 BLEU 得分结果。当样本数 m 足够大时（当 d_dot=512，m=256），Performer 与基础 Transformer 性能相当。实际上，当 d_key=64 时，m 的推荐值是 d_dot log（d_dot）=266。当 d_dot 相对较小时，该研究的 DPFP 模型优于线性 Transformer 和 Performer；在简单性和性能之间提供了一个很好的折衷。

语言模型

该研究使用标准 WikiText-103（Merity 等，2017）数据集进行实验。WikiText-103 数据集由维基百科的长文组成；训练集包含大约 28K 篇文章、总共 103M 个单词。这将产生约 3600 个单词的上下文文本块。验证集和测试集也包含类似的长依赖关系，分别有 218K 和 246K 个运行单词，对应 60 篇文章，词汇量约为 268K 个单词。下表 2 展示了在该研究更新规则下，WikiText-103 语言模型的困惑度结果。

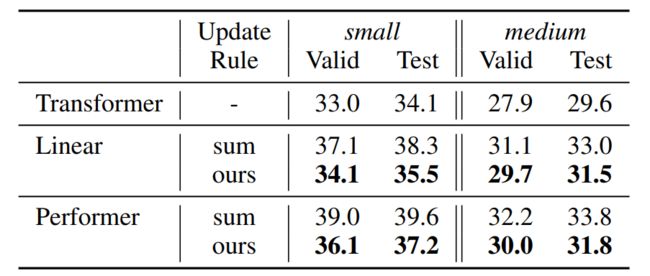
在下表 3 中，使用该研究更新规则下的 Transformer（medium 配置），在 WikiText-103 语言模型的困惑度结果。

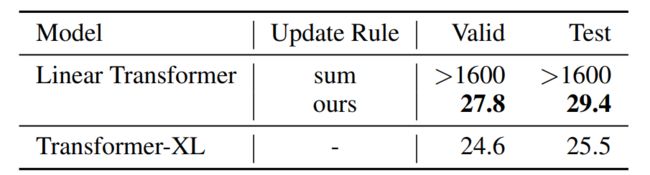
在下表 4 中，WikiText-103 语言模型在没有截断上下文的情况下训练和评估模型的困惑度，这与上表 2 中上下文窗口受到限制的情况相反。medium 配置既不用于位置编码，也不用于注意力标准化。

????

现在，在「知乎」也能找到我们了

进入知乎首页搜索「PaperWeekly」

点击「关注」订阅我们的专栏吧

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击「交流群」，小助手将把你带入 PaperWeekly 的交流群里。