用matlab和C++ ROS实现基于搜索的规划算法——A*，Dijkstra，DFS，BFS等

search based planning method

github源码
欢迎大家star和关注我呀~
从github里面可以直接看到动画哦~

我发布的仓库用于实现各种规划算法，包括基于搜索的算法、基于采样的算法等。我从中学到了很多，希望能对你有所帮助。

现在用MATLAB和C++，ROS实现了结果，之后会添加混合A*、state lattice planner、frenet坐标系下的规划等。

• the discrete planning/离散规划概述

离散可行规划The discrete feasible planning 使用状态空间(state-space)模型进行定义。主要含义是，地图中的每个不同情况/situation被称作一个状态state，用x表示，所以可能的状态集合为状态空间state space，用X表示。对于离散规划而言，要保证是该集合是可数的、有限的。
状态state的定义很关键。不要将无用信息加入到其中而增加复杂度。
动作action，用u表示，指的是能够从当前状态x到新状态x’的行为。而这个行为用状态转移函数 f 进行定义。也可以定义为有向图的形式。
x' = f(x,u)
状态空间是X，动作空间是U(x)。
初始状态X_I，目标状态X_G。
离散规划的统一表述形式：

• 通用的前向搜索算法框架：
  

其中，Q是指优先级队列(搜索算法中的唯一显著区别就是对Q进行排序的特定函数)，xI是起点，XG是终点集合。
这只是总的框架，有很多小细节，比如1. 如何判断x ∈XG; 2. 如何输出plan结果，即动作action序列; 3. 如何判断x’已经访问过visited (比如邻接矩阵，邻接表等); 4.如何定义排序方式等。

• 典型的forward search methods前向搜索算法：

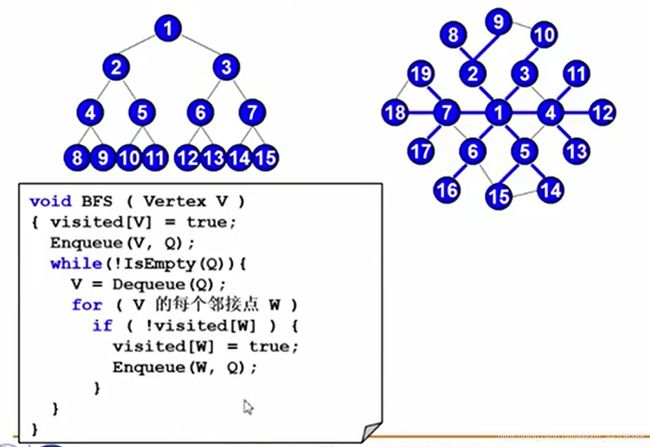
1. Breadth first广度优先搜索【不包含路径权重】
2. Depth first深度优先搜索【不包含路径权重】
3. Dijkstra’s algorithm【包含路径权重】
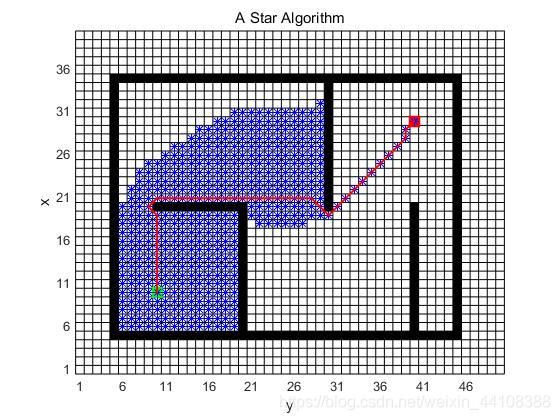
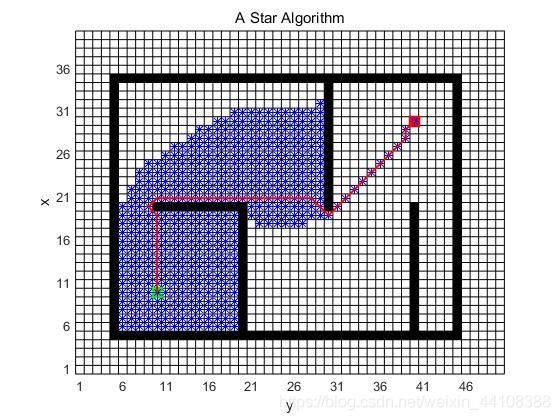
4. A-star【包含路径权重】
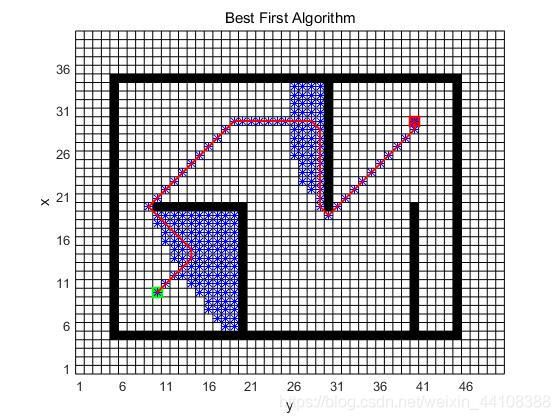
5. Best first【包含路径权重】

• 通用的后向搜索算法框架：
  

其中，Q是指优先级队列(搜索算法中的唯一显著区别就是对Q进行排序的特定函数)，xI是起点，XG是终点集合。
注意，动作序列为u^{-1，说明需要不是当前点能到那些邻接点，而是哪些邻接点能够到达当前点。对应的状态转移方程f}-1，即向后搜索。

• 通用的双向搜索算法框架：
  

其中，QI是指从起点出发的优先级队列(搜索算法中的唯一显著区别就是对Q进行排序的特定函数)，QG是指从终点出发的优先级队列，xI是起点，XG是终点集合。

ROS result

A star，A星：
同时考虑代价项g和启发项h。

Dijkstra算法：
只考虑代价项g。

Best First Search算法：
只考虑启发项h。

MATLAB result

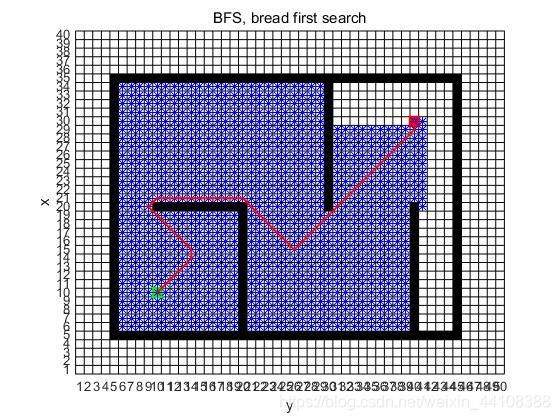
breadth first

可以用于求(每条路径权重为1的)最短路径。

• matlab程序实现:

  BreadFirstSearch文件夹里

• matlab实现结果：
  

• 思路逻辑

类似于树中的层序遍历的扩展：所以一定是随着边edge的长度增加而逐渐一层一层地访问下去。
步骤：
①将起点/根节点压入队列中，然后弹出，并将该弹出节点的邻接点压入到队列中；
②重复弹出节点并将弹出节点的尚未访问过的邻接点压入到队列中；
③直至队列为空，所有点都已经遍历完成(针对遍历)；对于找终点而言，就是到达终点结束。

• 数据结构思路：
  先进先出(FIFO, First-In First-Out) -> 优先级队列
  

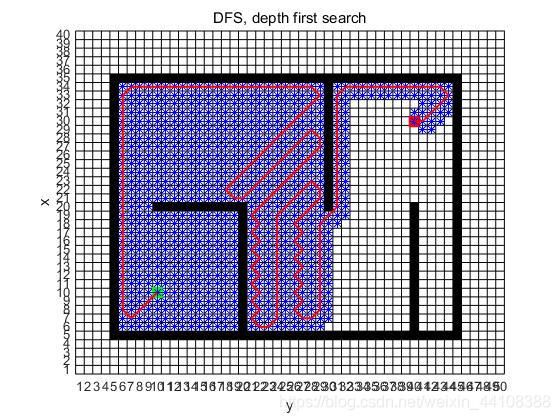
depth first

不可以用于求(每条路径权重为1的)最短路径，而只是用于搜索。

• matlab程序实现:

  DepthFirstSearch文件夹里

• matlab实现结果：
  

• 思路逻辑

类似于树中的先序遍历的扩展：所以一定是某一边的访问完了，再到另一边。
这个与A* 还不一样，因为A*有启发值，但是这个没有，就是随机地往某个方向走，走不通了再返回。
步骤：
①当前节点遍历，从邻接点中随机选择一个尚未遍历的顶点vertex继续遍历；
②如果当前节点的所有顶点都遍历过，就原路返回；【程序里用堆栈来实现】
③循环①②；
④直到回到起点(针对遍历)；对于找终点而言，就是到达终点结束。
深度优先搜索（Depth-First-Search），简称 DFS，最直观的例子就是走迷宫。
假设你站在迷宫的某个分岔路口，你想找到出口。你随意选择一个岔路口来走，走着走着发现走不通的时候就原路返回到上一个分岔路口，再选择另一条路继续走，直到找到出口，这种走法就是深度优先搜索的策略。

• 数据结构思路：
  后进先出(LIFO, Last-In, First-Out) -> 堆栈

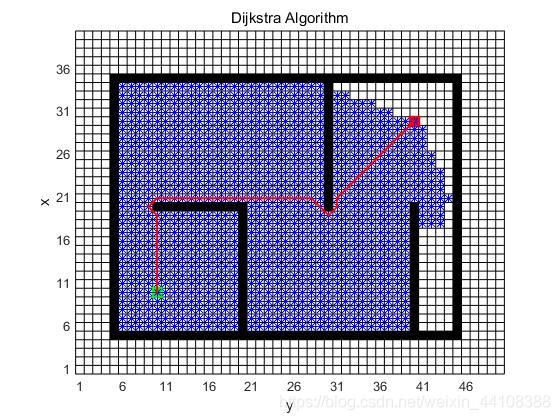
Dijkstra’s algorithm

可以用于求(带权重的)最短路径。
与BFS和DFS不同的是，需要进行代价更新。见“通用的前向搜索算法框架”中的第12行。

• matlab程序实现:

  DijkstraAlgorithm文件夹里

• matlab实现结果：
  

• 思路逻辑

步骤：
①初始化代价dist矩阵为inf，正无穷∞；将代价为0的起点放入优先级队列。
②如果优先级队列为空，则退出，说明搜索失败；否则，从优先级队列中选择一个最小代价的顶点vertex作为当前节点；
③遍历当前节点的周围搜索邻接点，如果该邻接点G代价小于原本的G代价，并且没有从队列中取出过，就更新代价dist矩阵，并放入优先级队列；否则更新优先级队列中的该已有的邻接点代价【程序里用最小堆（优先级队列）来实现】
④循环②③；
⑤直到到达终点。
注意：这里的dist就不能初始化为-1了，因为需要满足不等式 dist[W] + E < dist[W] ，所以这里dist[i]应该初始化为正无穷∞；同时起点的邻接点的dist初始化为对应的权重值。

• 数据结构思路：
  优先级队列

A star

可以用于求(带权重的)最短路径。
与Dijkstra’s algorithm不同的是，代价多了启发项。

• matlab程序实现:

  AStarAlgorithm文件夹里

• matlab实现结果：
  

• 思路逻辑

与Dijkstra’s algorithm几乎一模一样，只是代价值计算的时候多了启发项(到目标点的距离)：
可以看到程序中的对比：

1. Dijkstra’s algorithm

    V.Q = g_cost;
   

2. A star

    V.Q = g_cost+h_cost;
   

• 数据结构思路：
  优先级队列

Best first

不能保证一定可以找到(带权重的)最短路径。
与A star不同的是，代价只考虑启发项。

• matlab程序实现:

  BestFirstAlgorithm文件夹里

• matlab实现结果：
  

• 思路逻辑

与Dijkstra’s algorithm几乎一模一样，只是代价值计算的时候只考虑启发项(到目标点的距离)：
可以看到程序中的对比：

1. Dijkstra’s algorithm

    V.Q = g_cost;
   

2. A star

    V.Q = g_cost+h_cost;
   

3. Best first

    V.Q = h_cost;
   

• 数据结构思路：
  优先级队列

Bidirectional A Star Algorithm

从此开始有许多A*算法的变种，可以查看：
Amit’s A* Pages

• matlab程序实现:

  BidirectionalAStarAlgorithm文件夹里

• matlab实现结果：
  

• 思路逻辑
  双向A*，在原本的forward A*基础上考虑了同时从起点和终点出发，直到两者相遇。

• 数据结构思路：
  优先级队列

Anytime Repairing A*

ARA*: Anytime A* with Provable Bounds on
Sub-Optimality
Anytime Repairing A*(ARA*)的学习笔记

• 思路逻辑

ARA*是一种anytime planner，这种算法适合在有限的时间里做出尽可能最好的路径规划的场合，方法是先快速的得到一条次优路径，然后在时间允许的范围内不断地优化这条路径，可以证明在时间足够充裕的条件下，这个算法可以得到最优路径。
Weighted A*
Weighted A* 是对传统A*的改良，加入了膨胀因子（一般大于1）:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-WINYsCdN-1617089767018)()]
膨胀因子越大，搜索更容易朝着目标扩展，扩展的状态数量会越小，因此搜索时间会缩短；但是此算法会导致得到的路径并不一定是最优路径，比如距离最优。

ARA*
ARA* 则在 weighted A* 的基础上进行了发展，使得膨胀因子会变化，在时间允许的范围内，膨胀因子会越来越小直到变成1；在时间不够的时候，膨胀因子会尽可能的接近1，因为膨胀因子为1时，ARA* 算法接近于A* 算法，而A* 算法在理论上是最优的。
设置三个列表（open，closed, incons）的作用主要是为了使得ARA* 算法能够在每次降低膨胀因子后能够利用先前搜索所得到的一些结果，从而提高搜索效率。下面是ARA* 算法执行的基本流程：

1. 选取一个比较大的膨胀因子，快速的规划出一条次优的路径。
2. 在上一步规划的过程中会得到一个OPEN列表和INCONS列表,将二者合并为一个包含所有inconsistent状态的列表。
3. 将膨胀因子降低，在包含所有inconsistent状态的列表中进行搜索，规划出一个相对更优的路径。
4. 重复第2 3步,直到路径收敛(总的代价没有明显变化)或者膨胀因子降低为1为止。
5. 看是否规划出一条路径,返回成功/失败。

得到的一些结果，从而提高搜索效率。下面是ARA* 算法执行的基本流程：

1. 选取一个比较大的膨胀因子，快速的规划出一条次优的路径。
2. 在上一步规划的过程中会得到一个OPEN列表和INCONS列表,将二者合并为一个包含所有inconsistent状态的列表。
3. 将膨胀因子降低，在包含所有inconsistent状态的列表中进行搜索，规划出一个相对更优的路径。
4. 重复第2 3步,直到路径收敛(总的代价没有明显变化)或者膨胀因子降低为1为止。
5. 看是否规划出一条路径,返回成功/失败。