【机器学习】逻辑回归
上一章——正规方程
文章目录
- 线性回归并不全能
- 逻辑回归(对数几率回归)
-
- 决策边界
- 逻辑回归中的代价函数
-
- 为什么选择log?
- 损失函数的图像
- 如何在逻辑回归内实现梯度下降
(注意,从本章开始我更换为了新版的网课,可能会出现一些公式变动:
例如假设函数从 h θ ( x ) h_θ(x) hθ(x)变为了 f w , q ( x ) f_{w,q}(x) fw,q(x),在你看到公式可能与前面章节不对应时应当知道它是什么,毕竟不同的课程写法会有不同,但是原理都是相同的,只是换了个写法)
线性回归并不全能
在之前讲监督学习与无监督学习的时候,我们提到了一些问题应用,比如回归问题,在回归问题上我们是比较推荐使用线性回归的,但是还有一类问题:分类问题。我们之前提到过,分类问题希望能将给出的训练集划分为不同的类,再判断离散值结果该属于哪一类。
最典型的分类问题就是二元分类:其结果只有两种可能的类(classes)或者类别(catogories)
其结果往往是:“是”与“否”,“Y”与“N”,“T”与“F”,“1”与“0”等
比如我们之前提到的”是否为垃圾邮件“、”肿块是否为良性“都是属于这类问题 那么我们可以用线性回归来解决这类分类问题吗?答案是否定的,以下图为例
那么我们可以用线性回归来解决这类分类问题吗?答案是否定的,以下图为例

给出判断一个肿瘤是否为良性的训练集,如果我们想要用线性回归来处理这个问题就会变成下面这样
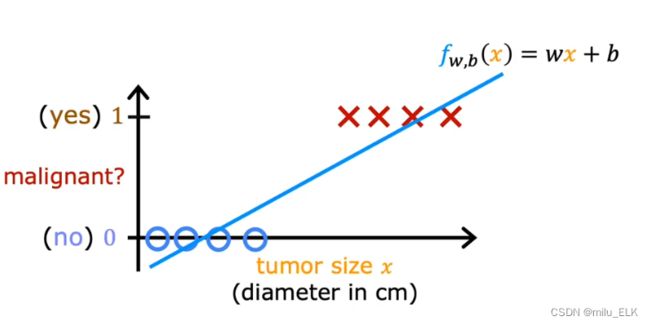
我们知道线性回归的目的并不是预测结果值是0,还是1这样的离散值,线性回归是为了预测连续值的输出,其结果不一定是”0“或”1“,而是[0,1]区间上乃至区间外的所有数,而分类问题的结果只有“0”和“1”。那么当我们把线性回归放到分类问题,想要预测出结果的类别是不太合适的
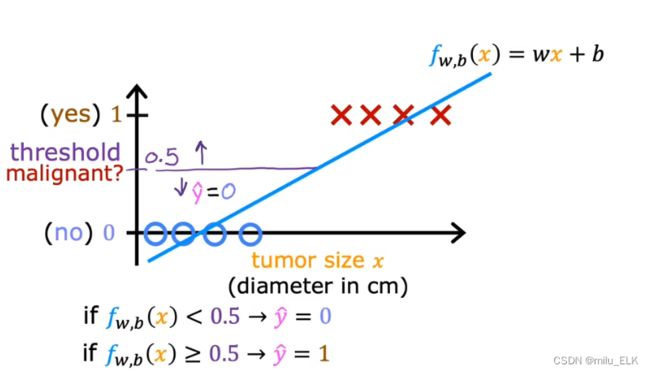
当然你可以自行决定一个判断阈值,当 预测的连续值 < 阈值 预测的连续值<阈值 预测的连续值<阈值时认为它是0,当 预测的连续值 > 阈值 预测的连续值>阈值 预测的连续值>阈值时认为它是1。我们当然可以这样做,但是如果你认为这样做能解决分类问题就大错特错了。
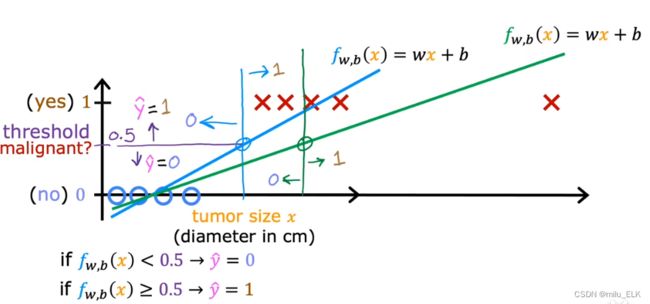 假设我们在右边很远的地方再加一个恶性样本,那么为了得到最佳拟合曲线,肯定要调整假设函数,那么此时阈值0.5所对应的位置就处于绿点处,那么我们再看,以上图中从左往右第一个红叉为例,在未添加新样本时,这个红叉我们认为它是恶性的;但是当添加新样本后,这个红叉反而成了良性。结果添加了1个新样本就改变了我们的预测结果,这显然是不合理的。因此线性回归并不适合解决分类问题,这也是为什么我们要选择逻辑回归来解决此类问题的理由
假设我们在右边很远的地方再加一个恶性样本,那么为了得到最佳拟合曲线,肯定要调整假设函数,那么此时阈值0.5所对应的位置就处于绿点处,那么我们再看,以上图中从左往右第一个红叉为例,在未添加新样本时,这个红叉我们认为它是恶性的;但是当添加新样本后,这个红叉反而成了良性。结果添加了1个新样本就改变了我们的预测结果,这显然是不合理的。因此线性回归并不适合解决分类问题,这也是为什么我们要选择逻辑回归来解决此类问题的理由
逻辑回归(对数几率回归)
注意逻辑回归和“逻辑”没有关系,只是因为它使用了Logistic函数(或者可以叫它Sigmoid函数)。
Logistic函数: g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1
用Logistic函数,我们拟合出来的曲线是这样的 并且我们重新绘制了如右图所示的图像,纵轴与函数交与0.5这个点,
并且我们重新绘制了如右图所示的图像,纵轴与函数交与0.5这个点,
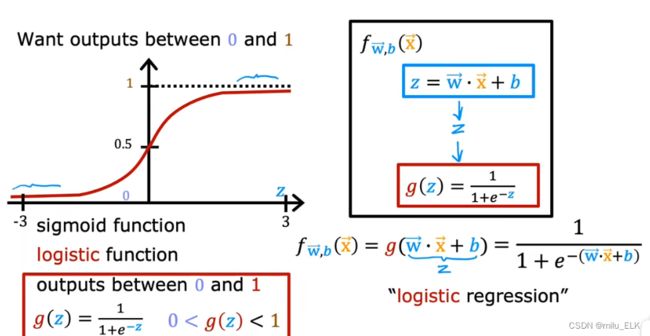 其中假设函数 f w , b ( x ) = g ( w ⋅ x + b ) = 1 1 + e − ( w ⋅ x + b ) f_{w,b}(x)=g(w\cdot x+b)=\frac{1}{1+e^{-(w\cdot x+b)}} fw,b(x)=g(w⋅x+b)=1+e−(w⋅x+b)1
其中假设函数 f w , b ( x ) = g ( w ⋅ x + b ) = 1 1 + e − ( w ⋅ x + b ) f_{w,b}(x)=g(w\cdot x+b)=\frac{1}{1+e^{-(w\cdot x+b)}} fw,b(x)=g(w⋅x+b)=1+e−(w⋅x+b)1
g ( z ) = 1 1 + e − z , z = w ⋅ x + b g(z)=\frac{1}{1+e^{-z}},z=w\cdot x+b g(z)=1+e−z1,z=w⋅x+b,从图像上不难看出 0 < g ( z ) < 1 0
但是有一个问题,Logistic函数的结果不也是连续值吗?为什么分类问题要使用Logistic函数呢?
首先,从Logistic函数的范围来看,Logistic函数的取值范围在(0,1),符合我们对分类问题只有两种不同真值的取值定义。
其次,Logistic函数的预测值虽然也是连续值,但它本质上是一个连续型的概率分布函数,也就是说我们可以将其预测值视为判断真值的概率

例如:当我们以y=1为条件,输入参数 x ⃗ , w ⃗ , b \vec x,\vec w,b x,w,b,得到的Logistic函数 f w ⃗ , b ⃗ ( x ) f_{\vec w,\vec b}(x) fw,b(x)相当于 P ( y = 1 ∣ x ⃗ ; w ⃗ , b ) P(y=1|\vec x;\vec w,b) P(y=1∣x;w,b),即当y=1时的概率,例如当前得到的预测值为0.7,就代表肿块为恶性的概率为0.7,反之良性的概率为0.3,概率之和为1。
当然,如果我们使用之前用过的“定义阈值来判断属于哪一类”的方法也是可以的,并且比线性回归要更直观

当 f = g ≥ 0.5 f=g\ge0.5 f=g≥0.5时,代表 z = w ⋅ x + b ≥ 0 z=w\cdot x +b \ge 0 z=w⋅x+b≥0,反之亦然,直接通过 w ⋅ x + b w\cdot x +b w⋅x+b的值就可以判断最终结果与阈值的关系。
决策边界
 在上图中,我们定义的 g ( z ) g(z) g(z)中的 z z z被称为决策边界,结合图像也很好理解——以z函数为边界,将训练集分为两个不同真值的部分。
在上图中,我们定义的 g ( z ) g(z) g(z)中的 z z z被称为决策边界,结合图像也很好理解——以z函数为边界,将训练集分为两个不同真值的部分。
当我们需要对分类问题的逻辑回归进行拟合时,应当做的就是正确地调整决策边界的系数值。
在决策边界的两边,分别将数据归为了不同的类,而如果有数据点落在了决策边界上,意味着这个数据的y=1和y=0的概率是几乎一致的。
 决策边界的函数选择当然也可以是非线性的,比如上图中用圆来作为决策边界,
决策边界的函数选择当然也可以是非线性的,比如上图中用圆来作为决策边界,
或者你也可以选择更加复杂的函数作为决策边界,只要满足拟合即可
逻辑回归中的代价函数
再讲回之前说过的代价函数,不过我们将线性回归的代价函数换成了这个式子
J ( w ⃗ , b ) = 1 m ∑ i = 1 m 1 2 ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) 2 J(\vec w,b)=\cfrac{1}{m}\displaystyle\sum_{i=1}^m \cfrac{1}{2}\bigg(f_{\vec w,b}(\vec x^{(i)})-y^{(i)}\bigg)^{2} J(w,b)=m1i=1∑m21(fw,b(x(i))−y(i))2
你可能注意到了,相比于旧版,式子中的变量向量化了,而且我们将 1 2 \cfrac{1}{2} 21放在了sum的里面

让我们画出逻辑回归的代价函数图像——它就像右图那样。对比线性回归的代价函数,明显线性回归的代价函数是一个凸函数,而线性回归则是非凸函数。如果我们想要在这样的代价函数上运行梯度下降法,显然不合理,因为它随时会落入局部最小值,而这是我们不想看到的。
这也说明了,如果逻辑回归沿用线性回归的最小二乘法来作代价函数是不可行的,因此,在逻辑回归中我们要学到一个新的代价函数:
J ( w ⃗ , b ) = 1 m L ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) J(\vec w,b)=\cfrac{1}{m}L\bigg(f_{\vec w,b}(\vec x^{(i)})-y^{(i)}\bigg) J(w,b)=m1L(fw,b(x(i))−y(i))
我们将 L ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) L\bigg(f_{\vec w,b}(\vec x^{(i)})-y^{(i)}\bigg) L(fw,b(x(i))−y(i))这个函数称之为损失函数,损失函数可以告诉我们模型在样本上的训练效果如何
其中 L ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) = { − l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) if y ( i ) = 1 − l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) if y ( i ) = 0 L\bigg(f_{\vec w,b}(\vec x^{(i)})-y^{(i)}\bigg)= \begin{cases} -log\bigg(f_{\vec w,b}(\vec x^{(i)})\bigg ) &\text{if } y^{(i)}=1 \\ -log\bigg(1-f_{\vec w,b}(\vec x^{(i)})\bigg ) &\text{if } y^{(i)}=0 \end{cases} L(fw,b(x(i))−y(i))=⎩ ⎨ ⎧−log(fw,b(x(i)))−log(1−fw,b(x(i)))if y(i)=1if y(i)=0
或者这个式子 L ( f w ⃗ , b ( x ⃗ ( i ) ) − y ( i ) ) = − y ( i ) l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) − ( 1 − y ( i ) ) l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) L\bigg(f_{\vec w,b}(\vec x^{(i)})-y^{(i)}\bigg)= -y^{(i)}log\bigg(f_{\vec w,b}(\vec x^{(i)})\bigg )-(1-y^{(i)})log\bigg(1-f_{\vec w,b}(\vec x^{(i)})\bigg ) L(fw,b(x(i))−y(i))=−y(i)log(fw,b(x(i)))−(1−y(i))log(1−fw,b(x(i)))
为什么选择log?
这个问题涉及到概率论的知识,作者本人概率论并不是很好,只是知道这是使用了极大似然估计,感兴趣的同学可以自行查阅资料
损失函数的图像
对于两种损失函数,我们画出它们两种函数的图像
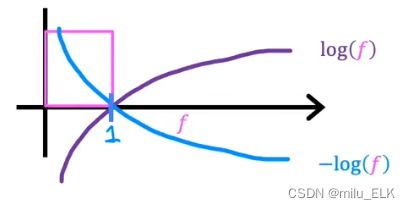
其中由于假设函数的取值范围是属于(0,1)的,因此我们只需看(0,1)区间上的图像即可

当 y ( i ) = 1 y^{(i)}=1 y(i)=1时,图像如图所示,其中纵轴代表了损失函数的损失,横轴代表了假设函数的值。
在第一种情况中,当假设函数值越接近0,损失函数损失越大,反之假设函数越接近1,损失函数损失值越小。
例如某肿瘤以真标签y=1为恶性,当其假设函数=0.9时,其损失函数较小,说明当假设函数为0.9(90%概率为恶性),我们判断它是恶性的损失是很小的。

那么反之,当 y ( i ) = 0 y^{(i)}=0 y(i)=0时,图像如图所示。我们依旧以刚才的例子为例,
例如某肿瘤以真标签y=0为良性,当其假设函数=0.9时(90%概率为恶性),那么在这种情况下认为该样本为良性,则它的损失是很大的,因此我们不该判断它为良性。
综上所述,损失函数代表了:如果预测值离y的真标签值越远,那么损失越大。我们鼓励算法选择损失更小的预测值来得到较高的准确率。
如何在逻辑回归内实现梯度下降
这是逻辑回归的代价函数:
J ( w ⃗ , b ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( f w ⃗ , b ( x ⃗ ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − f w ⃗ , b ( x ⃗ ( i ) ) ) ] J(\vec w,b)=-\cfrac{1}{m}\displaystyle\sum_{i=1}^m { \bigg[y^{(i)}log\bigg(f_{\vec w,b}(\vec x^{(i)})\bigg )+(1-y^{(i)})log\bigg(1-f_{\vec w,b}(\vec x^{(i)})\bigg )\bigg ]} J(w,b)=−m1i=1∑m[y(i)log(fw,b(x(i)))+(1−y(i))log(1−fw,b(x(i)))]
想要对其梯度下降,那么当然要求偏导了
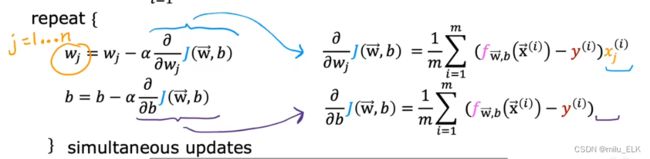

看起来似乎和线性回归的公式是一样的,不过还是有不同的,主要就是在于假设函数的定义不同了,在逻辑回归中假设函数是Logistic函数而非线性函数,不要忘记以下几点
- 观察图像,选择合适的学习率保证它快速收敛
- 你可以用向量化的逻辑回归梯度下降的速度更快
- 别忘了特征缩放
下一章——过拟合与正则化