论C语言中算法的重要性
最近一直在学数据结构与算法,深深的感受到我们学习语言,永远都只是一项工具,方法才是其中最重要的部分。这篇文章我将会通过几个例子来说明算法,也就是写程序的思路在程序中的重要意义。
目录
一、问题一(打印阶乘)
问题描述:
问题分析:
解决方案:
二、问题二(比较多项式计算时间)
问题描述:
问题分析:
解决方案:
一、问题一(打印阶乘)
问题描述:
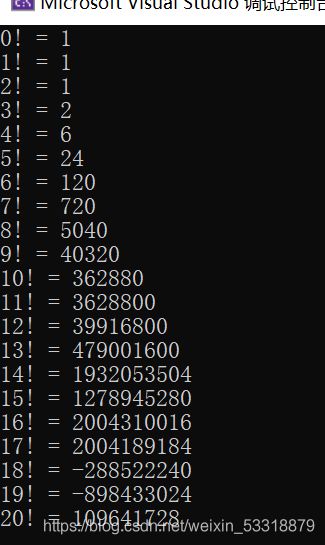
打印出数字一到数字20的阶乘
一开始,我总会多打印出一个1,这令我十分苦恼,并且从n等于13开始,数据就开始溢出
问题分析:
让我们分析一下问题,这里面存在着两个问题:
1.多打印出一个1
2.数据溢出
解决方案:
1.让我们检查一下结果,发现问题很有可能是循环的时候没有循环本身
for (i = 1; i < num; i++)//这句话明显错了
改成
for (i = 1; i <= num; i++) {//i的值要乘以它本身!
n = n * i;
}2.这里要引入C++中STL库的一个知识点
常规的32位整数只能够处理40亿以下的数。
如果遇到比40亿要大的数,就要用到C++的64位扩展。不同的编译器对64位整数的扩展有所不同。这个我也是听别人科普的,大家可以站内搜索一下。
优化后的代码如下:
#include
void main() {
__int64 fac(int num);
int n = 1;
int num;
for (num = 0; num <= 20; ++num) {
printf("%3d! = %I64d\n", num, fac(num));
}
}
__int64 fac(int num) {
register __int64 n = 1, i; //寄存器变量
for (i = 1; i <= num; i++) {//i的值要乘以它本身!
n = n * i;
}
return n;
} 二、问题二(比较多项式计算时间)
问题描述:
这里先科普几个测试代码中的知识点:
这个表示本程序开始计时:
start = clock();
本程序结束计时:
stop = clock();
clock tick :时钟打点
CLK_TCK:机器时钟每秒所走的时钟打点数
问题分析:
首先这个问题有两种算法:
直接算
p1 += (pow(x, i)/i);
把x当成公因式提出计算(秦九韶法)
p2 = 1.0/(a[i - 1])+ (x*p2);
然后我发现了三个问题:
1.测量不出时间
2.程序重复性高
3.第一种结果和第二种结果不一致
解决方案:
1.让被测函数重复运行多次,使得测出的总时钟打点间隔充分长,最后计算被测函数除以运行次数即可得出平均每次的运行时间
duration = ((double)(stop - start)) / CLK_TCK / MAXK;2.可以通过多设置几个函数,并调用函数解决问题
3.这是算法的问题
这个地方真的特别容易出错,我改了不知道多少遍。。。。。。
double f2(int n, double a[], double x) {
int i;
double p2 = 1.0/a[n];
for (i = n; i > 0; i--) {
p2 = 1.0/(a[i - 1])+ (x*p2);//算法思路出毛病了(数学)
}
return p2;
}总体的代码:
#include
#include
#include
clock_t start, stop;
double duration;
#define MAXN 101//数组里元素个数(多项式的系数),如果看n值需要减一,因为有a0
#define MAXK 1000//重复调用的次数
double f1(int n, double a[], double x)
{
double p1 = a[0];//a[0]都已经算出来了,循环从1开始
for (int i = 1; i <= n; i++) {
p1 += (pow(x, i)/i);
}
return p1;
}
double f2(int n, double a[], double x) {
int i;
double p2 = 1.0/a[n];
for (i = n; i > 0; i--) {
p2 = 1.0/(a[i - 1])+ (x*p2);//算法思路出毛病了(数学)
}
return p2;
}
double ceshijian()
{
stop = clock();//停止计时
duration = ((double)(stop - start)) / CLK_TCK / MAXK;//计算单次运行时间
printf("ticks=%f\n", (double)(stop - start));
printf("duration=%6.2e\n", duration);
return 0;
}
int main()
{
int i;
double a[MAXN];
for (i = 0; i < MAXN; i++) {
a[i] = (double)i;
}//输入的早就是i值了
a[0] = 1;
//不在测试范围内的准备工作写在clock()调用之前
start = clock();//开始计时
for (int i = 0; i < MAXK; i++)//重复调用
f1(MAXN - 1, a, 1.1);//被测函数,这里如果写数组的话就越界了,而且要调用某个值是不确定的,只能写a,因为要定义的就是a值
printf("第一种结果为%f\n", f1(MAXN - 1, a, 1.1));
ceshijian();
start = clock();//开始计时
for (i = 0; i < MAXK; i++)
f2(MAXN - 1, a, 1.1);//被测函数,这里如果写数组的话就越界了,而且要调用某个值是不确定的
printf("第二种结果为%f\n", f2(MAXN - 1, a, 1.1));
ceshijian();
return 0;
} 结果如下
明显看出第二种方法比第一种方法运行时间短了不少
因此,秦九韶法更加优越
算法是计算或解决问题的步骤,使用合理的算法可以缩短运行时间,使结果更加准确