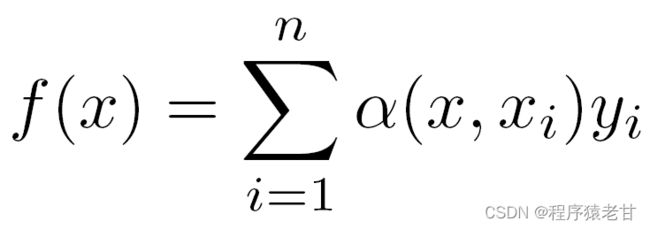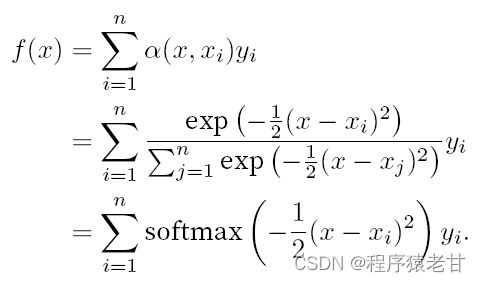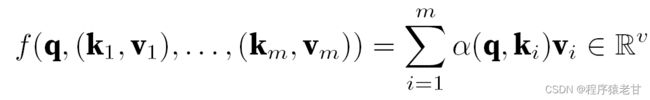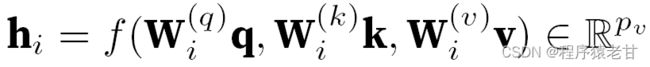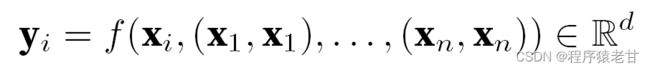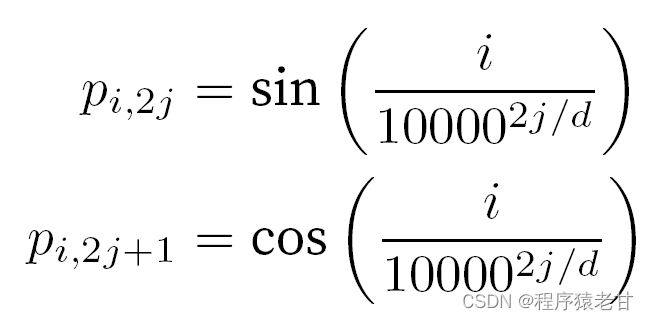点云深度学习系列博客(四): 注意力机制原理概述
目录
1. 注意力机制由来
2. Nadaraya-Watson核回归
3. 多头注意力与自注意力
4. Transformer模型
Reference
随着Transformer模型在NLP,CV甚至CG领域的流行,注意力机制(Attention Mechanism)被越来越多的学者所注意,将其引入各种深度学习任务中,以提升性能。清华大学胡世民教授团队近期发表在CVM上的Attention综述 [1],详细介绍了该领域相关研究的进展。对于点云应用,引入注意力机制,设计新的深度学习模型,自然是一个研究热点。本文以注意力机制为对象,概述其发展脉络,以及在点云应用领域的成功应用,为期望在该研究方向有所突破的同学,提供一点参考。
1. 注意力机制由来
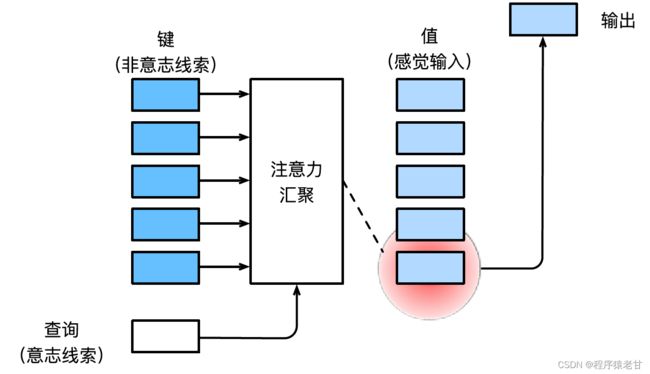
参考李沐老师深度学习教材 [2] 关于注意力机制部分的介绍,这里对注意力机制给出一个简单的解释。注意力机制即模拟人类视觉感知下,选择性地筛选信息进行接收和处理的机制。在信息筛选时,如果不提供任何自主性提示,即人在不做任何思考的情况下,阅读一段文本,观察一个场景,或听一段音频时,注意力机制偏重于异常信息,如一个黑白场景下穿红色衣服的女孩,或一段文字中的一个感叹号等。当引入自主性提示时,比如希望阅读和某个名词有关的语句,或有各对象关联的场景时,注意力机制引入这种提示,并且在信息筛选时,提高对这种信息的敏感度。为了对上述过程进行数学建模,注意力机制引入三个基本元素,即查询(Query),键(Key)和值(Value)。这三个元素共同构成了Attention Module的基本处理单元。键(Key)和值(Value)对应信息的输入和输出,查询(Query)对应的自主性提示。Attention Module基本处理单元如下图所示。
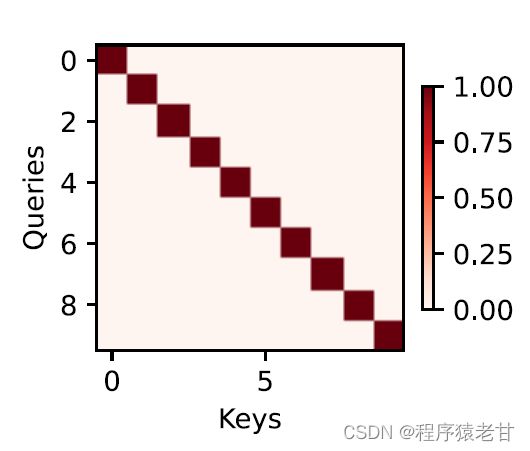
注意力机制通过注意力汇集,将查询和键结合在一起,实现对值的选择倾向。键和值是成对的,就像训练任务中的输入输出,是已知的数据分布,或者类别对应。注意力机制通过在注意力汇聚中输入查询,建立查询到每一个键的权重编码,得到查询与键的关系,进而指导对应值的输出。简而言之,就是当查询越接近某个键时,查询的输出结果就越接近键对应的值。该过程将注意力引入了更接近查询的键值对应关系,以指导符合注意力的输出。如果将查询与键对应建立一个二维的关系矩阵,当值相同时为1,不同时为0,其可视化结果可表示为:
2. Nadaraya-Watson核回归
这里介绍一个经典的注意力机制模型,即Nadaraya-Watson核回归 [3][4],用以理解注意力机制的基本运行逻辑。假设我们我们有一个受函数f控制的键值对应关系数据集{(x1,y1),(x2,y2),...(xi,yi)},学习任务是建立f,并指导对新的x键的求值。在这个任务中,(xi,yi)对应的就是键和值,输入的x表示查询,目标是获得其对应的值。按照注意力机制,需要通过考察x与键值对应关系数据集中每一个键值的相似关系,建立对其值的预测。当输入的x越接近某个xi键时,那么输出的值就越接近yi。这里对键值最简单的估计器是求平均:
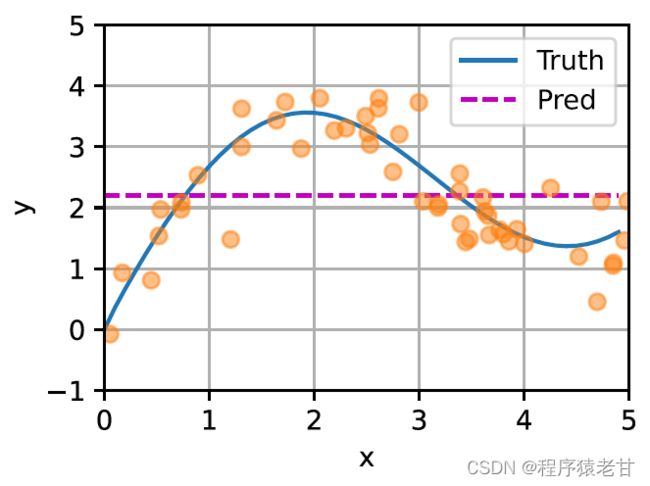
显然,这不是一个好主意。因为平均汇聚忽略了样本在键值分布上的偏离差异。如果将键值的差异引入到求值的过程,那么结果自然会变好。Nadaraya-Watson核回归即使用了这样的思路,提出了基于加权的求值方法:
K被认为是核,即被理解为衡量偏离差异的权重。如果将上面公式按照输入与键的差异权重,重写其自身公式,则可得到:
如果把上述权重替换为一个高斯核驱动的高斯权重,那么函数f即可表示为 :
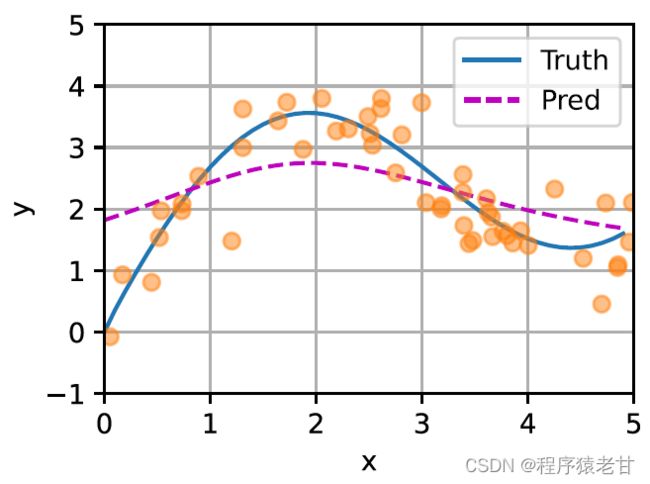
这里给出一个示意图,以对比平均汇聚(左图)和基于高斯核驱动的注意力汇聚(右图)推导出的不同f对于样本键值对的拟合情况。可以看到,后者的拟合性能会好很多。
上述模型是一个无参模型,对于带可学习参数的情况,建议阅读 [2] 注意力机制章节。这里所使用的高斯核及其对应的高斯权重,用来描述查询与键的关系。在注意力机制中,这种关系的量化表示,即为注意力评分。上述对查询值建立预测的过程,可以表示为对查询建立基于键值对的评分,通过对评分赋权,以获得查询值,表示为:
其中α表示权重,q表示查询,kv表示键值对。在教材 [2] 中还介绍了如何处理查询和键长度不匹配时间的加性注意力处理方法以及缩放点积注意力,用于定义注意力评分,这里不再详述。
3. 多头注意力与自注意力
1)多头注意力
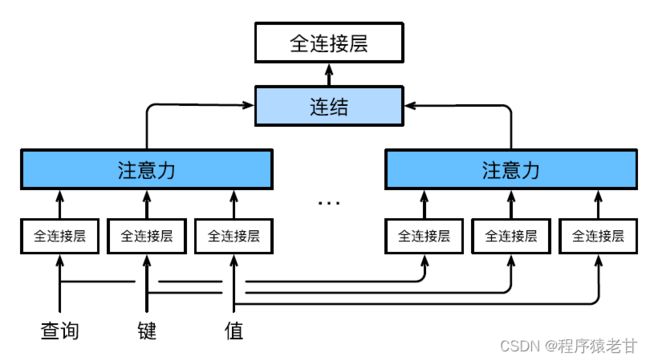
多头注意力用来组合使用查询、键值不同的子空间表示,基于注意力机制实现对不同行为的组织,来学习结构化的知识以及数据依赖关系。通过独立学习得到不同的线性投影,来变换查询、键和值。然后,将变换后的查询、键值并行地送到注意力汇聚中,然后将多个注意力汇聚的输出拼接在一起,并且通过另一个可以学习的线性投影进行变换,并产生最终输出。这种设计被称为多头注意力 [5]。下图展示了一个可学习的多头注意力模型:
这里给出每个注意力头的数学定义,给定查询q, 键k,值v,每个注意力头h的计算方法为:
这里的f可以是加性注意力和缩放点积注意力。多头注意力的输出经过另一个线性变换,以连接欸多个注意力机制输出,进而模仿更复杂的函数。
2)自注意力与位置编码
基于注意力机制,将NLP问题中的词元序列输入注意力汇聚,将一组词元同时充当查询、键值。每个查询都会关注所有的键值对并生成一个注意力输出。由于查询、键值均来自同一组输入,因此被称为自注意力机制。这里将给出基于自注意力机制的编码方法。
给定一个词元输入序列x1,x2,...,xn,对应的输出为一个相同的序列y1,y2,...,yn。y表示为:
这个公式起初我不是很理解。不过结合文本翻译的具体任务,就方便理解了。这里的意思是,一个词元某个位置上的元素,对应了输入和输出。即键值都是这个元素本身。我们需要学习的函数,即通过学习每个词与词元中的所有词汇的权重,来建立对值的预测。
在处理词元时,由于自注意力需要并行计算,而放弃了顺序操作。为了使用序列的顺序信息,可以在输入表示中添加位置编码来注入绝对的或相对的位置信息。通过对输入矩阵添加一个相同形状的位置嵌入矩阵,以实现绝对位置编码,其行列对应的元素表示为:
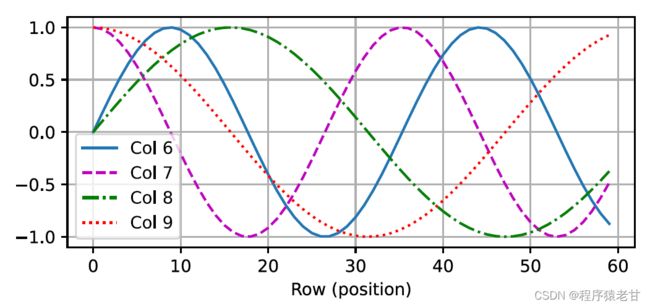
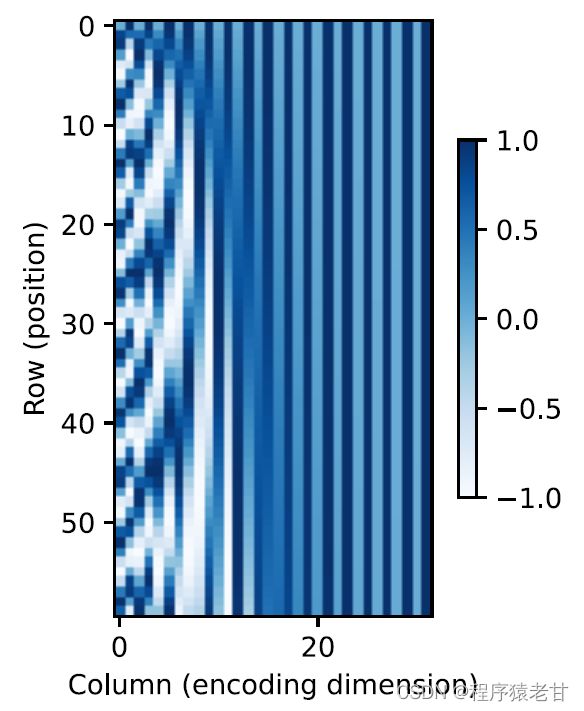
这种基于三角函数方法表示的位置嵌入矩阵元素并不直观。我们只知道编码维度与三角函数驱动的曲线频率存在一种关系。即每个词元内部不同维度的信息,其对应的三角函数曲线频率是不同的,如图表示:
似乎随着每个词元维度的升高,其间隔对应的频率会随之降低。为了搞清楚这种频率变化与绝对位置的关系,这里使用一个例子来解释。这里打印出0-7的二进制表示(右图为频率热图):
这里较高比特位的交替频率低于较低位。通过使用位置编码,实现词源不同维度基于频率变换的编码,进而实现对位置信息的添加。相对位置编码此处不再详述。
4. Transformer模型
终于到了激动人心的时候了!我们在理解了上述知识之后,就打好了学习Transformer的基础。相比之前依然依赖循环神经网络实现输入表示的自注意力模型,Transformer模型完全基于自注意力机制,没有任何卷积层或循环神经网络层。
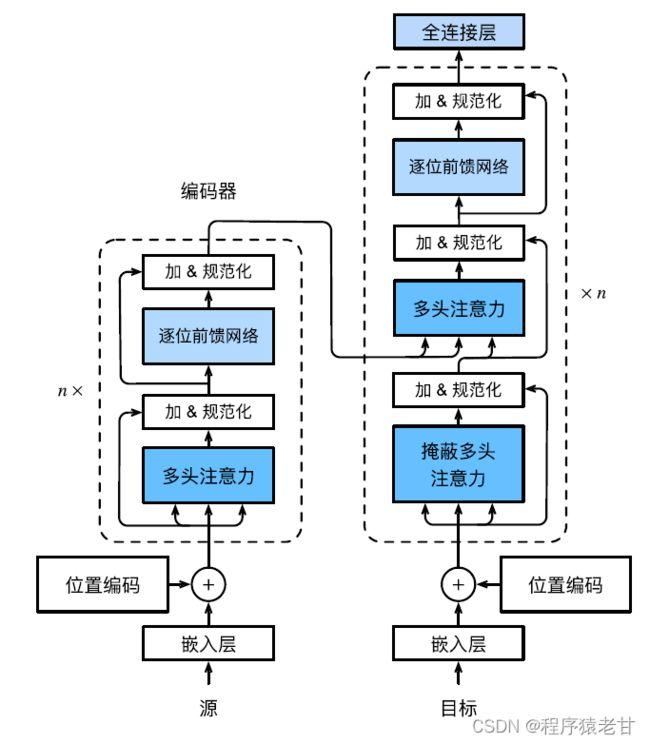
Transformer模型是一个编解码架构,整体架构图如下所示:
Transformer是由编码器和解码器组成的,基于自注意力模块构建,源(输入)序列和目标(输出)序列嵌入表示将加上位置编码,再分别输入到编码器和解码器中。 编码器是由多个相同的层叠叠加而成的,每个层都有两个⼦层。第一个子层是多头自注意力汇聚,第二个子层是基于位置的前馈网络。编码器层计算的查询,键,值均来自于上一层的输出。每个子层都使用了残差连接。解码器同编码器类似,也是由多个相同的层叠加⽽成,且使用了残差连接和层规范化。除了编码器中描述的两个子层外,解码器还添加了一个中间子层,称为编码器-解码器注意力层。该层中查询来自前一个解码器层的输出,⽽键和值来⾃整个编码器的输出。在解码器自注意力中,查询,键和值都来自上一个解码器层的输出。解码器中的每个位置只能考虑之前的所有位置。这种遮蔽注意力保留了自回归属性,确保预测仅依赖于已生成的输出词元。不同module的具体实现不再详述。
注:以上关于注意力机制的名词解释,原理介绍以及公式,主要参考李沐老师的教材 [2]。
基于上述注意力机制原理,针对点云处理任务的注意力机制深度学习模型被提出。我们将在下篇博客详细介绍相关工作,欢迎持续关注我的博客。
Reference
[1] MH. Guo, TX, Xu, JJ. Liu, et al. Attention mechanisms in computer vision: A survey[J]. Computational Visual Media, 2022, 8(3): 331-368.
[2] A. Zhang, ZC. Lipton, M. Li, and AJ. Smola. 动手学深度学习(Dive into Deep Learning) [B]. https://zh-v2.d2l.ai/d2l-zh-pytorch.pdf.
[3] EA. Nadaraya. On estimating regression[J]. Theory of Probability & Its Applications, 1964, 9(1): 141-142.
[4] GS. Watson. Smooth regression analysis. Sankhyā: The Indian Journal of Statistics, Series A, pp. 359‒372.
[5] A. Vaswani, N. Shazeer, N. Parmar, et al. Attention is all you need. Advances in neural information processing systems, 2017,5998‒6008.