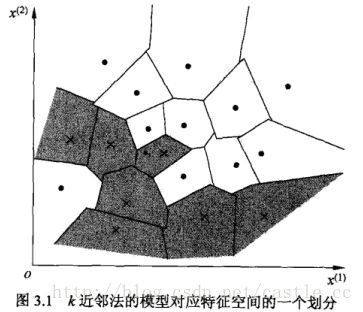
K近邻算法

给定一个训练数据集，对新的输入实例，在训练数据集中找到跟它最近的k个实例，根据这k个实例的类判断它自己的类（一般采用多数表决的方法）
距离度量： 一般使用欧氏距离，也可以使用其他距离。
k值的选择：k较小，容易被噪声影响，发生过拟合。k较大，较远的训练实例也会对预测起作用，容易发生错误。
分类决策规则：多数表决（应该也可以根据距离使用带权重的表决方式）。
主要问题：如何快速的进行k近邻搜索。

最近邻(1-NN)算法图示：

5-NN算法图示：

k近邻算法的实现：kd树

T = [[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]]


class node:
    def __init__(self, point, split):
        self.left = None
        self.right = None
        self.point = point
        self.parent = None
        self.split = split;
        pass

    def set_left(self, left):
        if left == None: pass
        left.parent = self
        self.left = left

    def set_right(self, right):
        if right == None: pass
        right.parent = self
        self.right = right


def median(lst):
    m = len(lst) // 2
    return lst[m], m


def build_kdtree(data, d):
    data = sorted(data, key=lambda x: x[d])
    p, m = median(data)
    tree = node(p, d)

    del data[m]

    if m > 0: tree.set_left(build_kdtree(data[:m], not d))
    if len(data) > 1: tree.set_right(build_kdtree(data[m:], not d))
    return tree


def distance(a, b):
    print (a, b)
    return ((a[0] - b[0]) ** 2 + (a[1] - b[1]) ** 2) ** 0.5


def search_kdtree(tree, d, target, root):
    if target[d] < tree.point[d]:
        if tree.left != None:
            return search_kdtree(tree.left, not d, target, root)
    else:
        if tree.right != None:
            return search_kdtree(tree.right, not d, target, root)

    def update_best(t, best):
        if t == None: return
        t = t.point
        d = distance(t, target)
        if d < best[1]:
            best[1] = d
            best[0] = t


    best = [tree.point, distance(tree.point, target)]
    while (tree.parent != None and tree != root):
        split = tree.parent.split
        if(best[1] > abs(target[split] - tree.parent.point[split])):
            update_best(tree.parent, best)
            tempBest = None
            if(tree.point[split] < tree.parent.point[split]):
                if(tree.parent.right != None):
                    tempBest = search_kdtree(tree.parent.right, tree.parent.right.split, target, tree.parent.right)
            else:
                if(tree.parent.left != None):
                    tempBest = search_kdtree(tree.parent.left, tree.parent.left.split, target, tree.parent.left)
            if(tempBest != None and tempBest[1] < best[1]):
                best = tempBest
        tree = tree.parent
    return best


kd_tree = build_kdtree(T, 0)
print (search_kdtree(kd_tree, 0, [5, 2], kd_tree))

上述代码只给出了寻找二维空间最邻近点的解法。

kd树的原理可参考：详解KDTree

knn算法不仅可以用于分类， 还可以用于回归， 回归的值由k个最近的样例值决定。

参考：
[1] 统计学习方法， 李航 著
[2] k近邻法