分类算法 - k近邻算法(原理、kd树)

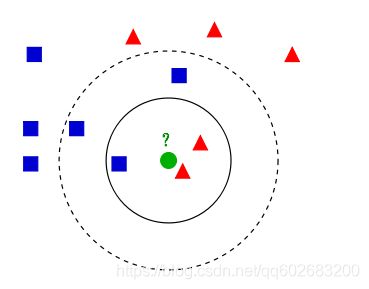
1. 算法概述

k近邻算法解决分类问题一种常见的方法，其主要思路是，根据给定距离度量，在训练集中找到目标点最近的k个样本的分类结果，经过分类规则，预测目标样本的分类。

2. 模型三要素

从算法概述可以得到3个重要的要素：距离、k值以及分类规则。

2.1 距离度量

k近邻一般特征空间为N维实数空间，一般采用欧氏距离，但在一些情况下，也可以采用其他距离，下面介绍一些常见的距离度量。

欧式距离

欧式距离又称为欧几里得距离，定义在欧几里得空间中，$(x_1,x_2,...,x_n)$与$(y_1,y_2,...,y_n)$之间的欧式距离定义为：
$$d(X,Y)=\sqrt{(x_1-y_1{)}^2+(x_2-y_2{)}^2+...+(x_n-y_n{)}^2}$$

曼哈顿距离

曼哈顿距离是城市区块距离，实际上是在欧几里得空间两点之间连线在固定直角坐标系投影的距离总和，$(x_1,x_2,...,x_n)$与$(y_1,y_2,...,y_n)$之间的曼哈顿距离定义为：
$$d(X,Y)=|x_1-y_1|+|x_2-y_2|+...+|x_n-y_n|$$

切比雪夫距离

切比雪夫距离是一种超凸度量，$(x_1,x_2,...,x_n)$与$(y_1,y_2,...,y_n)$之间的切比雪夫距离定义为：
$$d(X,Y)=max(|x_1-y_1|,|x_2-y_2|,...,|x_n-y_n|)$$
直观解释：在国际象棋中，国王可以移动到相邻8个方格的任意一个，那么国王从$(x_1,y1)$移动到$(x_2,y_2)$最少需要走$max(|x_1-y_1|,|x_2-y_2|)$步，切比雪夫距离是一种类似的度量

闵可夫斯基距离

闵式距离不是一种距离而是一组距离的定义，给出了普遍的定义，$(x_1,x_2,...,x_n)$与$(y_1,y_2,...,y_n)$之间的闵可夫斯基距离定义为：
$$d(X,Y)=\sqrt[p]{\sum _{k=1}^n|x_i-y_i{|}^n}$$
p是一个可变参数，
当p=1，闵式距离就是曼哈顿距离
当p=2，闵式距离就是欧式距离
当p->$\infty$，闵式距离就是切比雪夫距离

马氏距离

马氏距离可以应对高维线性分布数据中，各维度间非独立同分布的问题，是用于衡量两个样本集之间相似度的度量。假设有M个样本$X=(x_1,x_2,...,x_m{)}^t$, 协方差矩阵为S，均值$\mu =({\mu }_1,...,{\mu }_m)$

• 单个数据点的马氏距离（X和$\mu$的距离）：
  $$D_M(X)=\sqrt{(X-\mu {)}^T{S}^{-1}(X-\mu )}$$
• 数据点X,Y之间的马氏距离：
  $$D_M(X)=\sqrt{(X-Y{)}^T{\Sigma }^{-1}(X-Y)}$$

马氏距离与特征的量纲无关，排除变量之间的相关性的干扰。

余弦夹角

几何中余弦夹角是用来衡量两个向量方向的差异，定义如下‘：
$$cos\theta =\frac{\sum x_i{y}_i}{\sqrt{\sum {x_i}^2}\sqrt{\sum y_i^2}}$$’
余弦夹角的取值范围在[-1,1]之间，夹角余弦值越大两个向量夹角越小，重合为1，相反为-1。

常用的距离还有巴氏距离（两个离散或连续概率分布的相似性）、Jaccard相似度（2个集合的相似度）、皮尔逊相关系数等

2.2 k值选择

k值过小： 学习器容易忽略数据本身的分布，学习了噪声数据,并且容易导致模型出现过拟合（试想k=1的情况）

k值过大：学习器可能会忽略数据样本中大量有用的信息（试想k=N的情况）

选取规则：采用交叉验证来获取最优的k值

2.3 分类规则

多数投票表决：即由k个近邻范围内的训练样本中，多数类决定目标样例的类别，事实上，多数投票表决可以使得误分率最小

参考:k近邻法学习笔记

2. 算法流程

• 对训练集合测试集的特征进行标准化
• 计算测试数据与每条训练数据的距离
• 计算结果进行递增排序
• 选取与测试数据最近的k个训练样本
• 根据k个样本的类别进行多数投票表决
• 返回k个样本中出现最多的类别作为测试数据的类别

3.优缺点分析

优点：

• 算法简单易懂、可解释性强
• 可用于离散型数据和离散型数据

缺点：

• 需要计算目标点与所有训练数据的距离，计算开销大
• 必须保存全部数据，对存储要求高
• 样本不平衡时，可能导致较大偏差

4.算法优化

4.1 距离加权

为避免因一个样本数据过多导致误判，可以考虑对距离进行加权，增大距离小的样本权重，可以考虑如下加权方式：

【反函数】
即距离的倒数，但如果距离非常接近会导致权重很大，为了避免出现无穷大的情形，建议在距离上加一个常量
$$w=\frac{1}{distance+c}$$
注意，这种方法对噪声比较敏感

【高斯函数】

高斯函数：
$$f(x)=a{e}^{-\frac{(x-b{)}^2}{2c^2}}$$
x为距离，a、b、c为指定实数，高斯加权的好处是距离为0时权重不会吴庆大，随着距离变大，权重变小但不会为0

4.2 kd - tree

k-d树是一种对k维空间样本点进行存储的二叉树，可以实现快速搜索，从而实现减少距离计算次数。

4.2.1 kd树的构造

构造kd树相当于不断用垂直于坐标轴的超平面将k维空间划分，构造一系列的k维超矩形区域。

以下是书上描述的构造方法：

不太好理解，下面给一个例子：

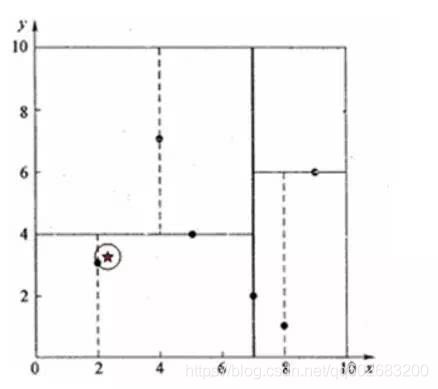
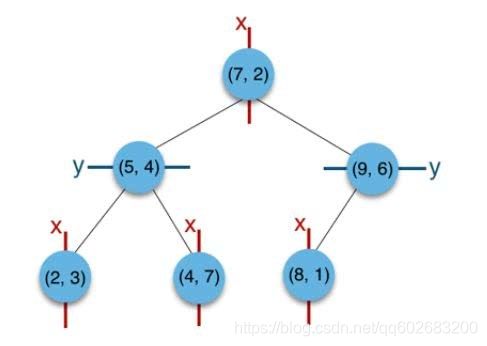
以二维为例，假设有集合集合(2,3)，(5,4)，(9,6)，(4,7)，(8,1)，(7,2)，

• 首先构建根节点:
  x方向上集合的排序为(2,3)，(4,7)，(5,4)，(7,2)，(8,1)，(9,6), 取x方向上中位数的点(7,2)作为根节点
• 构建根节点的左子树
  x<=7小的点在左子树，x>7的点在右子树，即(2,3)，(4,7)，(5,4)在(7,2)的左子树，(8,1)，(9,6)在(7,2)的右子树
• 下一层左节点划分
  下一层的划分维度为y，(2,3)，(4,7)，(5,4)中y中值点(5,4)作为父节点，(2,3)为其左子节点，(4,7)为其右子节点
• 下一层右节点划分
  同样的，点集合(8,1)，(9,6)此时的切分维度也为y，中值为(9,6)作为分割平面，(8,1)在其左子树。

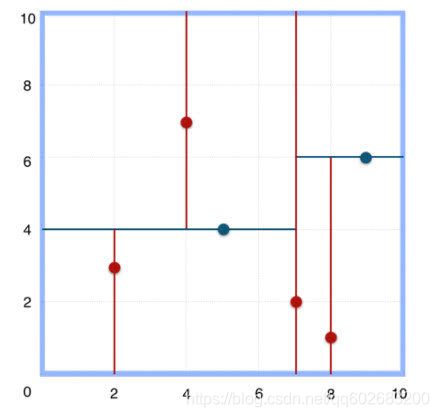
划分的二维空间如下：

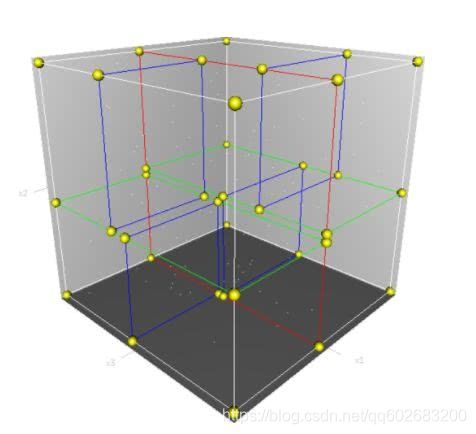
三维的情况类似，划分出来的就不是一个矩形平面而是一个立体的空间：

4.2.2 利用kd树进行近邻搜索

以下是书上给的步骤：


还是不太好理解，大体思路是：

• 先找到最近的叶子节点
• 进行回溯，判断父节点是否为近邻样本点
• 判断父节点的另一子节点是否为近邻样本点

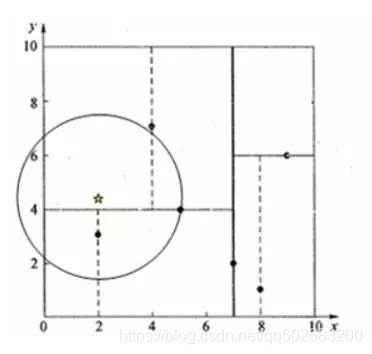
下面给两个例子，

例子1：与右子空间无交集情形

• 目标点为(2.1, 3.1)
• 首先顺着kd树找到目标点所在区域对应的叶子节点(2,3)
• 回溯至其父节点(5,4)
• 由于最邻近点肯定位于以查询点为圆心且通过叶子节点的圆域内，发现该圆并不和超平面y = 4交割，因此节点在该父节点的其他子节点空间中无有距离查询点更近的数据点，因此不用进入（5,4）节点右子空间中去搜索。
• 继续回溯到上一层（7,2），也不相交，不需要搜索（7,2）右子空间
• （7,2）为根节点，搜索终止

例子2：与右子空间有交集情形

• 首先顺着kd树找到最近的叶子节点(4,7), 计算其与目标查找点的距离
• 回溯到(5,4)，与目标点间的距离更小，当前最近邻点变成（5,4）
• 以目标点为圆心，以目标点到当前最近邻点的距离为半径作圆
• 该圆和（5,4）左子空间有交集，需回溯至(2,3)叶子节点
• (2,3)距离比(5,4)近，当前最近邻点更新为(2,3)，最近距离更新为1.5
• 回溯至(7,2)，作圆，不和x = 7分割超平面交割
• (7,2)为根节点，搜索终止

寻找k个最近邻点的算法与之类似：

5. 模型参数

sklearn.neighbors.KNeighborsClassifier(n_neighbors=5, weights=’uniform’, 
algorithm=’auto’, leaf_size=30, p=2, metric=’minkowski’, metric_params=None, n_jobs=None, **kwargs)

参数解释：

• n_neighbors： default=5
  k值,

• weights: {‘uniform’, ‘distance’} 或者自定义, default=’uniform’
  距离权重，uniform等权重，distance权重和距离呈反比，callable自定义权重array

• algorithm：{‘auto’, ‘ball_tree’, ‘kd_tree’, ‘brute’}, default=’auto’
  计算方式
  auto - 自动选择最合适的方式
  ball_tree - ball_tree算法
  kd_tree - kd_tree算法
  brute - 蛮力算法

• leaf_size: default = 30
  停止建子树的叶子节点阈值

• p,metric: 距离度量参数
  p取1为曼哈顿距离，p取2为欧式距离，默认取2
  metric默认取闵可夫斯基距离

• metric_params：距离度量其他附属参数
  一般用不上

n_jobs:并行处理任务数

6. 算法实现

from sklearn.datasets import load_iris
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import classification_report
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
import matplotlib.pyplot as plt

# 获取数据
iris = load_iris()
iris_data = iris.data
iris_target = iris.target

# 数据处理
##标准化
std = StandardScaler()
iris_data_std = std.fit_transform(iris_data)

## 划分训练集、测试集
x_train, x_test, y_train, y_test = train_test_split(iris_data_std,iris_target,test_size = 0.25)

# 模型训练
def knn_train(k):
    knn = KNeighborsClassifier(n_neighbors=k)
    knn.fit(x_train,y_train)
    y_pred = knn.predict(x_test)
    return y_pred

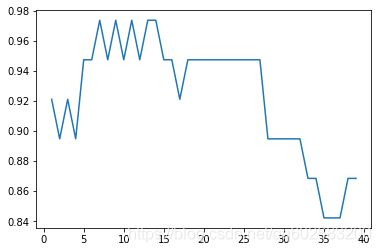
# 结果
accuracy_score_list = []    
for k in range(1,40):
    y_pred = knn_train(k) 
    accuracy_score_list.append(accuracy_score(y_test,y_pred))
    
plt.plot(range(1,40),accuracy_score_list)

k取值超过一定范围后，模型效果变差，结果变化如下图：

7. 参考

1. 从K近邻算法、距离度量谈到KD树、SIFT+BBF算法
2. KNN(k近邻算法)最最最全面总结
3. k最邻近算法——加权kNN
4. 机器学习系列之——Knn算法 kd树详解
5. KNN算法和kd树详解（例子+图示）