第十届蓝桥杯大赛第二场省赛赛题 C++ 大学C组

试题A：求和

问题描述

   小明对数位中含有2、0、1、9的数字很感兴趣，在1到40中这样的数包括1、2、9、10至32、39和40，共28个，他们的和是574。
  请问，在1到2019中，所有这样的数的和是多少？

算法设计

• 用函数将数位中含有2、0、1、9的数字筛选出来，并进行求和即可。

# include 
using namespace std;
bool number(int x);
int main(){
    int n;
    cin >> n;
    long long int sum = 0;
    for (int i = 1; i <= n; ++i) {
        if(number(i)){
           sum = sum + i;
        }
    }
    cout << sum << endl;
    return 0;
}
bool number(int x){
    while(x){
        int temp = x % 10;
        if(temp == 0 || temp == 2 || temp == 1 || temp == 9){
            return true;
        }
        x = x / 10;
        temp = x;
    }
    return false;
}

输入：

40

输出：

574

输入：

2019

输出：

1905111

试题B：矩形切割

问题描述

  小明有一些矩形的材料，他要从这些矩形材料中切割出一些正方形。
  当他面对一块矩形材料时，他总是从中间切割一刀，切出一块最大的正方形，剩下一块矩形，然后再切割剩下的矩形材料，直到全部切为正方形为止。
  例如，对于一块两边分别为5和3的材料（记为$5\times 3$），小明会依次切出$3\times 3$、$2\times 2$、$1\times 1$、$1\times 1$ 共4个正方形。
  现在小明有一块矩形的材料，两边长分别是2019和324。请问小明最终会切出多少个正方形？

算法设计

• 类似去做一个完全平方数的求和，但需要注意的是长方形长和宽有个迭代变换的关系。

# include 
using namespace std;
int solve(int x,int y);
int main(){
    int c,k;
    cin >> c >> k;
    int c_1 = max(c,k);
    int k_1 = min(c,k);
    cout << solve(c_1,k_1) << endl;
}
int solve(int c,int k){
    int count = 0;
    long long int sum = 0;
    long long int s = c * k;
    for (int i = k; s >= sum; --i) {
        sum = sum + k * k;
        int temp = k;
        k = min(k,c-k);
        c = max(temp,c-k);
        count++;
        if(k == 1 || k == 0){
            break;
        }

    }
    return count+(s-sum);
}

输入：

2019 324

输出：

21

试题C：年号子串

问题描述

   小明用字母A对应数字1，B对应2，以此类推，用Z对应26,。对于27以上的数字，小明用两位或更长位的字符串来对应，例如AA对应27，AB对应28，AZ对应52，LQ对应329。
  请问2019对应的字符串是什么？

算法设计

• 类似于26进制的转换，但要注意的是，0在其中没有对应字母。答案为BYQ。

试题D：质数

问题描述

   我们知道第一个质数是2、第二个质数3、第三个质数是5…请你计算第2019个质数是多少？

算法设计

• 编写素数判断函数，找到第2019个素数。

# include 
using namespace std;
bool check(long long int x);
int main(){
    int count = 0;
    long long int i = 2;
    while(count <= 2019){
        if(check(i)){
            count++;
            if(count == 2019){
                break;
            }
            else{
                i++;
            }
        }
        else{
            i++;
        }
    }
    cout << i;
    return 0;
}
bool check(long long int x){
    if(x == 1){
        return false;
    }
    else{
        for (int i = 2; i <= sqrt(x); ++i) {
            if(x % i == 0){
                return false;
            }
        }
        return true;
    }
}

输出：

17569

试题E：最大降雨量

问题描述

   由于沙之国长年干旱，法师小明准备施展自己的一个神秘法术来求雨。
   这个法术需要用到他手中的49张法术符，上面分别写着1至49这49个数字。法术一共持续7周，每天小明都要使用一张法术符，法术符不能重复使用。
   每周，小明施展法术产生的能量为这7周7张法术符上数字的中位数。法术施展完7周后，求雨将获得成功，降雨量为7周能量的中位数。
   由于干旱太久，小明希望这次求雨的降雨量尽可能大，请求出最大值是多少？

算法设计

• 要想7周能量的中位数尽可能大，那么每周的中位数要尽可能大，这里我们往后面取，7个数，也就是从小到大第4个数为中位数，前面三个数我们取最小，后面三个数我们取最大，即1、2、3、47、48、49，47为第1周的中位数，依次类推。
  
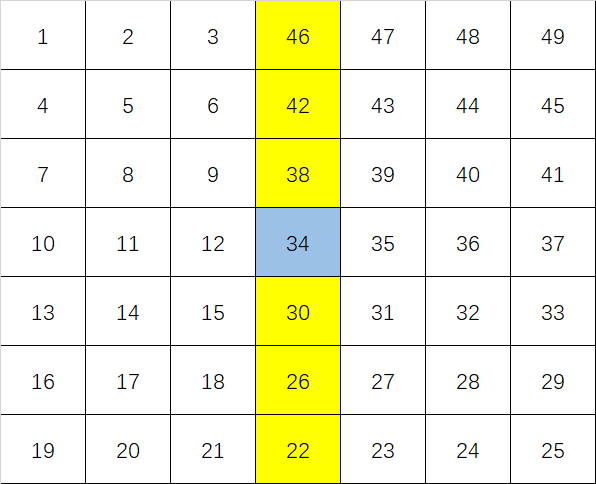
• 由此得到每周最大中位数，7周中位数为34，答案为34。

试题F：旋转

问题描述

  图片旋转是对图片最简单的处理方式之一，在本题中，你需要对图片顺时针旋转90度。
  我们用一个$n\times m$的二维数组来表示一个图片，给定初始图片，请计算旋转后的图片。

输入格式

  输入的第一行包含两个整数$n$和$m$，分别表示行数和列数。
  接下来$n$行，每行$m$个整数，表示给定的图片，图片中的每个元素（像素为一个值为0至255之间的整数）。

输出格式

  输出$m$行$n$列，表示旋转后的图片。

算法设计

• 实际上是矩阵的转置，但是需要注意的是矩阵不一定是方阵，要将$m\times n$变为$n\times m$

# include 
using namespace std;
int main(){
    int m,n;
    cin >> m >> n;
    int num[m][n];
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            cin >> num[i][j];
        }
    }
    int ans[n][m];
    for (int i = 0; i < m; ++i) {
        for (int j = 0; j < n; ++j) {
            ans[j][m-i-1] = num[i][j];
        }
    }
    for (int i = 0; i < n; ++i) {
        for (int j = 0; j < m; ++j) {
            cout << ans[i][j] << " ";
        }
        cout << endl;
    }
}

输入：

3 4
1 3 5 7
9 8 7 6
3 5 9 7

输出：

3 9 1
5 8 3
9 7 5
7 6 7

试题G：外卖店优先级

问题描述

  “饱了么”外卖系统中维护着N家外卖店，编号1 ~ N。每家外卖店都有一个优先级，初始时（0时刻）优先级都为0。
  每经过1个时间单位，如果外卖店没有订单，则优先级会减少1，最低减到0；而如果外卖店有订单，则优先级不减反加，每有一单优先级加2。
  如果某家外卖店某时某刻优先级大于5，则会被系统加入优先缓存中，如果优先级小于等于3，则会被清除出优先缓存。
  给定T时刻以内的M条订单信息，请你计算T时刻时有多少外卖店在优先缓存中。

输入格式

  第一行包含3个整数N、M和T。
  以下M行每行包含两个整数ts和id，表示ts时刻编号id的外卖店收到一个订单。

输出格式

  输出一个整数代表答案。

算法设计

# include 
using namespace std;
int main(){
    int N,M,T;
    cin >> N >> M >> T;
    int a,b;
    vector<vector<int> > dd(M+1,vector<int>(M+1)); //创建各时刻下各店铺的订单数，dd[M+1][M+1]，并初始化为0
    vector<pair<int,int > > pr(N+1); //创建店铺优先级数组
    vector<bool> check(N+1,false); //创建检查数组，并初始化为false
    for (int i = 1; i <= N; ++i) { //店铺优先级数组初始化
        pr[i].first = i;
        pr[i].second = 0;
    }
    for (int i = 0; i < M; ++i) { //订单数量
        cin >> a >> b;
        dd[a][b]++;
    }
    for (int i = 1; i <= T; ++i) {
        vector<pair<int,int > > copy(pr); //复制一个优先级列表
        for (int j = 0; j < dd[i].size(); ++j) {
            if(dd[i][j] != 0){
                pr[j].second += dd[i][j] * 2; //每一个订单获得两个优先级
            }
        }
        for (int j = 1; j <= N; ++j) { //更新优先级
            if(pr[j].second - copy[j].second == 0 && copy[j].second != 0){ //对比上一时刻店铺优先级
                pr[j].second -= 1;
            }
        }
        for (int i = 1; i <= N; ++i) { 
            if(pr[i].second > 5 && !check[i]){ // 判断店铺是否加入优先缓存
                check[i] = true;
            }
            else if(pr[i].second <= 3 && check[i]){ //判断店铺是否被移出优先缓存
                check[i] = false;
            }
        }
    }
    int count = 0;
    for (int i = 1; i <= N; ++i) {
        if(check[i]){
            count++;
        }
    }
    cout << count << endl;
    return 0;
}

输入：

2 6 6
1 1
5 2
3 1
6 2
2 1
6 2

输出：

1

试题H：人物相关性分析

问题描述

  小明正在分析一本小说中的人物相关性。他想知道在小说Alice和Bob有多少次同时出现。
  更准确的说，小明定义Alice和Bob“同时出现”的意思是：在小说文本中Alice和Bpb之间不超过K个字符。

输入格式

  第1行包含一个整数K。
  第2行包含一行字符串，只包含大小写字母、标点符号和空格。长度不超过1000000.

输出格式

  输出一个整数，表示Alice和Bob同时出现的次数。

算法设计

• 移动窗口算法实现。

#include 
using namespace std;
string s; //定义全局变量s
bool checkA(int i, int len); //判断是否为Alice, i为下标, len为字符串长度
bool checkB(int i, int len); //判断是否为Bob, i为下标, len为字符串长度
int main(){
    int k; //定义k
    cin >> k; //输入k
    getchar(); //吃回车
    getline(cin, s); //整行输入字符串s
    int len = s.length(); //定义len为s的长度
    vector<int> Alice, Bob; //定义数组记录名字出现时的下标
    for(int i = 0; i < len; i++){ //遍历字符串
        if(s[i] == 'A' && checkA(i, len)){ //如果字符为'A'判断是否为Alice
            Alice.push_back(i); //添加下标到数组
            i += 5; //跳过名字(名字后后空格,无需担心循环中的i++)
        }
        else if(s[i] == 'B' && checkB(i, len)){ //如果字符为'B'判断是否为Bob
            Bob.push_back(i); //添加下标到数组
            i += 3; //跳过名字
        }
    }
    int As = Alice.size(), Bs = Bob.size(); //As与Bs分别为两数组元素个数
    int bl = 0, br = 0; //bl与br分别为窗口左右边界
    long long ans = 0; //定义答案（最后一个评测点会超过int范围）
    for(int i = 0; i < As; i++){ //遍历Alice数组元素
        while(bl < Bs && Bob[bl] < Alice[i] - k - 3)    bl++; //维护窗口左边界
        while(br < Bs && Bob[br] <= Alice[i] + k + 5)   br++; //维护窗口右边界
        ans += br - bl; //答案加上窗口中元素个数
    }
    cout << ans << endl; //输出答案
    return 0;
}
bool checkA(int i, int len){ //判断是否为Alice, i为下标, len为字符串长度
    if(len - i < 5)  return false;//如果字符串长度减去A出现的下标没有5个，说明不存在
    return s[i+1] == 'l' && s[i+2] == 'i' && s[i+3] == 'c' && s[i+4] == 'e';
}
bool checkB(int i, int len){ //判断是否为Bob, i为下标, len为字符串长度
    if(len - i < 3)  return false;
    return s[i+1] == 'o' && s[i+2] == 'b';
}

输入：

20
This is a story about Alice and Bob. Alice wants to send a private message to Bob.

输出：

2

试题I：等差数列

问题描述

  数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列，只记得其中N个整数。
  现在给出这N个整数，小明想知道包含这N个整数的最短的等差数列有几项？

输入格式

  输入的第一行包含一个整数N。
  第二行包含N个整数$A_1$、$A_2$、…、$A_N$。

输出格式

  输出一个整数表示答案

算法设计

• 找出相邻数间最大差值，从差值到1依次遍历，直到找到公差。

# include 
using namespace std;
bool contrast(vector<int> x,vector<int> y); //y是否为x的子集
int main() {
    vector<int> num;
    int N;
    cin >> N;
    int temp;
    for (int i = 0; i < N; ++i) { //存储数组
        cin >> temp;
        num.push_back(temp);
    }
    sort(num.begin(), num.end());
    int max = 0;
    for (int i = 0; i < N - 1; ++i) { //取相邻数最大差值
        temp = num[i + 1] - num[i];
        if (max < temp) {
            max = temp;
        }
    }
    vector<int> cs; //创建等差数组
    cs.push_back(num[0]);
    for (int i = max; i > 0 ; --i) {
        int j = 0;
        while(*(cs.end()-1) < num[N-1]){ //创建的等差数组最大值大于等于数组的最大值
            cs.push_back(cs[j] + i);
            j++;
        }
        if(contrast(cs,num)){ //若输入数组为等差数组的子集
            cout << cs.size() << endl; //输出数组大小
            break;
        }
        else{
            cs.clear(); //清空数组
            cs.push_back(num[0]);
        }
    }
    return 0;
}

bool contrast(vector<int> x,vector<int> y){
    int n = y.size();
    for (int i = 0; i < n; ++i) {
        auto iter = find(x.begin(), x.end(), y[i]); //查找
        if(iter == x.end()){
            return false;
        }
    }
    return true;
}

输出：

5
2 6 4 10 20

输出：

10

试题J：扫地机器人

问题描述

  小明公司的办公区有一条长长的走廊，由N个方格区域组成。
  走廊内部署了K台扫地机器人，其中第i台在第$A_i$个方格区域中。
  已知扫地机器人每分钟可以移动到左右相邻的方格中，并将该区域清扫干净。
  请你编写一个程序，计算每台机器人的清扫路线，使得
  1. 他们最终都返回出发方格
  2. 每个方格区域都至少被清扫一遍
  3. 从机器人开始行动到最后一台机器人归位花费的时间最少
  注意多台机器人可以同时清扫同一方块区域，它们不会互相影响。输出最少花费的时间。

输入格式

  第一行包含两个整数N和K。
  接下来K行，每行一个整数$A_i$。

输出格式

  输出一个整数表示答案。

算法设计

• 使用二分法查找。

# include 
using namespace std;
int n,k;
vector<int> a;
bool check(int x);
int main(){
    cin >> n >> k;
    int temp;
    for (int i = 0; i < k; ++i) {
        cin >> temp;
        a.push_back(temp);
    }
    sort(a.begin(),a.end());
    int l,r;
    l = 0;
    r = n;
    while(l < r){
        int mid = l + (r-l)/2;
        if(check(mid)){
            r = mid;
        }
        else{
            l = mid+1;
        }
    }
    cout << (l-1) * 2 << endl;
    return 0;
}

bool check(int x){
    int left = 0;
    for (int i = 0; i < k; ++i) {
        if(a[i] - x <= left){
            if(a[i] < left){
                left = a[i] + x -1;
            }
            else{
                left = left + x;
            }
        }
        else{
            return false;
        }
    }
    if(left < n){
        return false;
    }
    else{
        return true;
    }
}

输入：

10 3
5
2
10

输出：

6