R-Drop: Regularized Dropout for Neural Networks 论文笔记（介绍，模型结构介绍、代码、拓展KL散度等知识）

---

前言

R-Drop——神经网络的正则化DropOut

一、摘要

摘要：Dropout是一种强大且广泛应用的深度神经网络的调整训练的技术。尽管效果很好，但由于Dropout所带来的随机性导致了训练和实际之间的不一致性。在本文中，我们引入了一种简单的一致性训练策略来正则化dropout，即R-Drop，它强制dropout生成的不同子模型的输出分布彼此一致。具体来说，对于每个训练样本，R-Drop最小化dropout采样的两个子模型输出分布之间的双向kl -散度。理论分析表明，R-Drop降低了上述不一致性。（有关于KL散度请查看文章末尾附录介绍，有关于DropOut的详细介绍请看下方链接）
Dropout的深入理解（基础介绍、模型描述、原理深入、代码实现以及变种）

二、R-Drop介绍

背景：在训练神经网络的过程中，过拟合时有发生，DropOut技术可以解决过拟合问题并且提高模型的泛化能力，但是DropOut的随机性导致了训练和实际应用中模型的不一致性。（即训练阶段采用随机删除单元的方法，而在实际应用的过程中采用的是不删除任何单元的完整模型）本论文中介绍了一种简单的方法来正则化由DropOut引起的不一致性，称为R-Drop。

定义：R-Drop通过最小化两个分布之间的双向KL散度，来使得同一份数据的两个子模型输出的两个分布保持一致。与传统的神经网络训练中的DropOut策略相比，R-Drop只是增加了一个没有任何结构改变的kl散度损失。

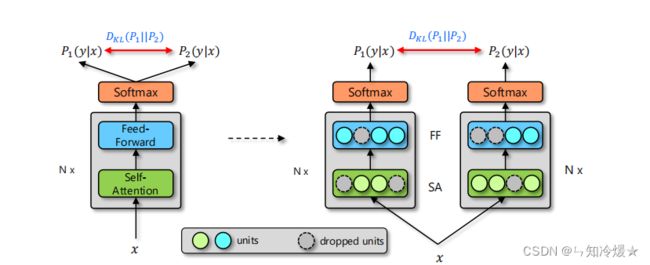
整体框架结构：R-Drop的总体框架如下，以Transformer为例，左图显示了一个输入x将遍历模型两次，得到两个分布p1和p2，右图显示了dropout产生的两个不同的子模型。（如图右侧所示，输出预测分布P1和输出分布P2在各层删除的单元各不相同，因此，对于同一输入数据对（$x_i$, $y_i$）, P1和P2的分布是不同的，我们的R-Drop方法试图通过最小化同一样本这两个输出分布之间的双向KL散度来正则化模型预测)。

三、R-Drop公式详解

训练的数据对集合：n为训练样本的个数，（$x_i$，$y_i$）代表数据对，例如在自然语言处理中，x代表源语言，y代表目标语言。
$$D=\{(x_i,y_i){\}}_i^n$$

模型预测的分布： P1和P2
$$P_1^w(y_i|x_i)$$ $$P_2^w(y_i|x_i)$$

分布P1和P2的KL散度：
$$D_{KL}(p1|p2)$$

输出分布P1和P2的双向KL散度：
$$L_{KL}^i=\frac{1}{2}(D_{KL}(P_1^w(y_i|x_i)||P_2^w(y_i|x_i))+D_{KL}(P_2^w(y_i|x_i)||P_1^w(y_i|x_i)))$$

对数似然损失函数：
$$L_{NLL}^i=-log{P}_1^w(y_i|x_i)-log{P}_2^w(y_i|x_i)$$

对于数据对集合$\{(x_i,y_i){\}}_i^n$，训练的目标是最小化函数： 其中α为控制双向KL散度目标函数的系数。

$$L^i=L_{NLL}^i+\alpha L_{KL}^i=-log{P}_1^w(y_i|x_i)-log{P}_2^w(y_i|x_i)+\frac{\alpha }{2}(D_{KL}(P_1^w(y_i|x_i)||P_2^w(y_i|x_i))+D_{KL}(P_2^w(y_i|x_i)||P_1^w(y_i|x_i)))$$

四、R-Drop计算流程

• 训练数据对集合$D=\{(x_i,y_i){\}}_i^n$
• 得到模型参数w
• 使用参数w来初始化模型
• 如果没有收敛，则以下步骤循环执行：

---

• 随机抽样数据对 $(x_i,y_i)$
• 重复输入 数据两次，并且得到两个输出分布
• 计算对数似然损失函数
• 计算双向KL散度
• 通过最小化函数 $L^i$ 来更新模型参数。

---

附录0：代码

import torch.nn.functional as F

# define your task model, which outputs the classifier logits
model = TaskModel()

def compute_kl_loss(self, p, q, pad_mask=None):
    
    p_loss = F.kl_div(F.log_softmax(p, dim=-1), F.softmax(q, dim=-1), reduction='none')
    q_loss = F.kl_div(F.log_softmax(q, dim=-1), F.softmax(p, dim=-1), reduction='none')
    
    # pad_mask is for seq-level tasks
    if pad_mask is not None:
        p_loss.masked_fill_(pad_mask, 0.)
        q_loss.masked_fill_(pad_mask, 0.)

    # You can choose whether to use function "sum" and "mean" depending on your task
    p_loss = p_loss.sum()
    q_loss = q_loss.sum()

    loss = (p_loss + q_loss) / 2
    return loss

# keep dropout and forward twice
logits = model(x)

logits2 = model(x)

# cross entropy loss for classifier
ce_loss = 0.5 * (cross_entropy_loss(logits, label) + cross_entropy_loss(logits2, label))

kl_loss = compute_kl_loss(logits, logits2)

# carefully choose hyper-parameters
loss = ce_loss + α * kl_loss

附录一：熵以及信息熵

熵：用于描述不确定性，表示系统混乱的程度，越整齐熵也就越小，越混乱不确定的程度越大，熵也就越大，因此整个环境会自发的朝着混乱的方向发展，也就是熵增原理。

信息熵含义：信息熵表示随机变量不确定的程度。一件事情发生的概率越高，那么他的确定性也就越大，那么它的熵也就越小。信息熵常常被作为一个系统的信息含量的量化指标。

性质：信息熵非负。当一件事发生的概率为1时，信息就没有不确定，那么它的熵就是0。
公式：p(x)代表的是事件x发生的概率。
$$H(X)=-\sum _{x\in X}p(x)logp(x)$$

总结：那些接近确定性的分布（输出几乎可以确定）具有较低的熵，那些接近均匀分布的概率分布具有较高的熵。

附录二：KL散度（相对熵）

定义：在机器学习领域，KL散度用来度量两个函数（概率分布）的相似程度或者相近程度，是用来描述两个概率分布差异的一种方法，也叫做相对熵。也就是说KL散度可以作为一种损失，来计算两者之间的概率差异。
公式：
$$KL(p||q)=\sum p(x)log\frac{p(x)}{q(x)}=\sum p(x)(logp(x)-logq(x))$$

性质：

• KL散度的值始终>=0，当且仅当P(x)=Q(x)时等号成立。
• KL散度并不是一个对称量，KL(p||q)不等于KL(q||p)

双向KL散度定义：通过交换这两种分布的位置以间接使用整体对称的KL散度。

$$双向KL散度=0.5\ast KL(A|B)+0.5\ast KL(B|A)$$

附录三：JS散度

定义：KL散度是不对称的，训练神经网络会因为不同的顺序造成不一样的训练结果，为了克服这个问题，提出了JS散度。

$$JS(P1||P2)=\frac{1}{2}KL(P1||\frac{P1+P2}{2})+\frac{1}{2}KL(P2||\frac{P1+P2}{2})$$

性质：

• JS散度的值域范围是[0，1]，相同为0，相反则为1，相比于KL，对相似度的判断更加准确了。
• JS散度是一个对称量，JS(p||q)等于JS(q||p)， 对称可以让散度度量更加准确，下边是证明代码。

import numpy as np
import math


# 离散随机变量的KL散度和JS散度的计算方法

def KL(p, q):
    # p,q为两个list，里面存着对应的取值的概率，整个list相加为1
    if 0 in q:
        raise ValueError
    return sum(_p * math.log(_p / _q) for (_p, _q) in zip(p, q) if _p != 0)


def JS(p, q):
    M = [0.5 * (_p + _q) for (_p, _q) in zip(p, q)]
    return 0.5 * (KL(p, M) + KL(q, M))


def exp(a, b):
    a = np.array(a, dtype=np.float32)
    b = np.array(b, dtype=np.float32)
    a /= a.sum()
    b /= b.sum()
    print(a)
    print(b)
    print(KL(a, b))
    print(JS(a, b))


if __name__ == '__main__':
    # exp1
    print('exp1: Start')
    print(exp([1, 2, 3, 4, 5], [5, 4, 3, 2, 1]))
    print('exp1: End')

    # exp2
    # 把公式中的第二个分布做修改，假设这个分布中有某个值的取值非常小，就有可能增加两个分布的散度值
    print('exp2: Start')
    print(exp([1, 2, 3, 4, 5], [1e-12, 4, 3, 2, 1]))
    print(exp([1, 2, 3, 4, 5], [5, 4, 3, 2, 1e-12]))
    print('exp2: End')

    # exp3
    print('exp3: Start')
    print(exp([1e-12,2,3,4,5],[5,4,3,2,1]))
    print(exp([1,2,3,4,1e-12],[5,4,3,2,1]))
    print('exp3: End')

输出：
exp1: Start
[0.06666667 0.13333334 0.2 0.26666668 0.33333334]
[0.33333334 0.26666668 0.2 0.13333334 0.06666667]
0.5216030835963031
0.11968758856917597
None
exp1: End
exp2: Start
[0.06666667 0.13333334 0.2 0.26666668 0.33333334]
[1.e-13 4.e-01 3.e-01 2.e-01 1.e-01]
2.065502018456509
0.0985487692550548
None
[0.06666667 0.13333334 0.2 0.26666668 0.33333334]
[3.5714287e-01 2.8571430e-01 2.1428572e-01 1.4285715e-01 7.1428574e-14]
9.662950847122168
0.19399530008415986
None
exp2: End
exp3: Start
[7.1428574e-14 1.4285715e-01 2.1428572e-01 2.8571430e-01 3.5714287e-01]
[0.33333334 0.26666668 0.2 0.13333334 0.06666667]
0.7428131560123377
0.19399530008415986
None
[1.e-01 2.e-01 3.e-01 4.e-01 1.e-13]
[0.33333334 0.26666668 0.2 0.13333334 0.06666667]
0.38315075574389773
0.0985487692550548
None
exp3: End

• 将第一个实验与第二个实验做对比，可以看出KL散度的波动比较大，而JS的波动相对小。
• 如果将第二个实验和第三个实验做对比，可以发现KL散度在衡量两个分布的差异时具有很大的不对称性。如果后面的分布在某一个值上缺失，就会得到很大的散度值；但是如果前面的分布在某一个值上缺失，最终的KL散度并没有太大的波动。这个demo可以清楚地看出KL不对称性带来的一些小问题，而JS具有对称性，所以第二个实验和第三个实验的JS散度实际上是距离相等的分布组。

附录四：互信息

定义：互信息衡量的是两种度量间相互关联的程度，极端一点来理解，如果X,Y相互独立，那么互信息为0，因为两者不相关；而如果X,Y相互的关系确定（比如Y是X的函数），那么此时X,Y是“完全关联的”。
公式：
$$I(X；Y)=\sum _{x，y}p(x，y)log\frac{p(x，y)}{p(x)p(y)}=H(X)-H(X|Y)=H(Y)-H(Y|X)$$

参考文章：

原文github代码地址.
论文地址.
信息熵：什么是信息熵？
某乎：信息熵是什么？
信息熵的简单理解
信息熵？互信息？KL散度？
交叉熵损失函数（Cross Entropy Loss）
KL散度与JS散度
互联网各大公司职级和薪资一览
《论文阅读》R-Drop:Regularized Dropout for Neural Network

机器学习:Kullback-Leibler Divergence(KL散度)以及R-dropout函数的通俗讲解
初学机器学习：直观解读KL散度的数学概念

---

总结

不太好理解，泪目。‍♂️