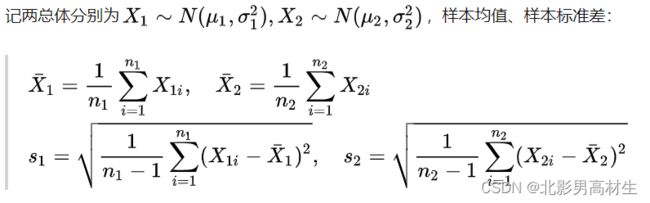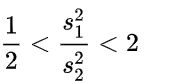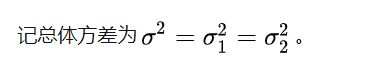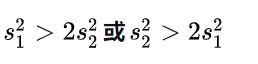数据分析之T检验
1、定义:
t检验,亦称student t检验(Student’s t test),主要用于样本含量较小(例如n < 30),总体标准差σ未知的正态分布。 t检验是用t分布理论来推论差异发生的概率,从而比较两个平均数的差异是否显著。它与f检验、卡方检验并列。来源:百度百科
用于统计量服从正态分布,但方差未知的情况。
T检验分析时,当样本量较大时,很少考虑T检验的使用条件。由中心极限定理可知,只要样本量足够大,其样本均数的抽样分布仍然是正态的。即:只要数据分布不是强烈的偏态,一般而言T检验都是适用的。当样本例数n较小时,一般要求样本取自正态本体。
t检验的前提是要求样本服从正态分布或近似正态分布,不然可以利用一些变换(取对数、开根号、倒数等等)试图将其转化为服从正态分布是数据,如若还是不满足正态分布,只能利用非参数检验方法。不过当样本量大于30的时候,可以认为数据近似正态分布。
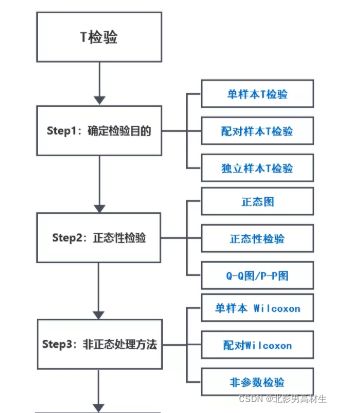
2、T检验的分类
2.1、单样本T检验
检验单个变量的均值与目标值之间是否存在差异,如果总体均值已知,样本均值与总体均值之间差异显著性检验属于单样本t检验。
2.1.1 目的
检验单样本的均值是否和已知总体的均值相等(主要用于比较一组数据与一个特定数值之间的差异情况)
2.1.2 要求
- 总体方差未知,否则就可以利用Z检验(也叫U检验,就是正态检验)
- 正态数据或近似正态
2.1.3 原假设H0与备择假设H1
- H0:样本均值与总体均值相等
- H1:样本均值与总体均值不等
2.1.4 python 中的单样本T检验 ttest_1samp
from scipy import stats
import numpy as np
np.random.seed(7654567) # 保证每次运行都会得到相同结果
# 均值为5,方差为10
rvs = stats.norm.rvs(loc=5, scale=10, size=(50,2))
stats.ttest_1samp(rvs, [1, 2])
返回结果:
Ttest_1sampResult(statistic=array([ 2.0801775 , 2.44893711]), pvalue=array([ 0.04276084, 0.01795186]))
分别显示两列数的t统计量和p值。由p值分别为0.042和0.018,当p值小于0.05时,认为差异显著,即第一列数的均值不等于1,第二列数的均值不等于2。
- 不拒绝原假设——均值等于5
stats.ttest_1samp(rvs, 5.0)
Ttest_1sampResult(statistic=array([-0.68014479, -0.04323899]), pvalue=array([ 0.49961383, 0.96568674]))
- 拒绝原假设——均值不等于5
stats.ttest_1samp(rvs, 0.0)
Ttest_1sampResult(statistic=array([ 2.77025808, 4.11038784]), pvalue=array([ 0.00789095, 0.00014999]))
- 第一列数均值等于5,第二列数均值不等于0
stats.ttest_1samp(rvs,[5.0,0.0])
Ttest_1sampResult(statistic=array([-0.68014479, 4.11038784]), pvalue=array([ 4.99613833e-01, 1.49986458e-04]))
- 第一行数均值等于5,第二行数均值不等于0
#axis=0按列运算,axis=1按行运算
stats.ttest_1samp(rvs.T,[5.0,0.0],axis=1)
- 将两列数据均值分别与5.0和0.0比较,得到4个t统计量和p值
stats.ttest_1samp(rvs,[[5.0],[0.0]])
Ttest_1sampResult(statistic=array([[-0.68014479, -0.04323899],[ 2.77025808, 4.11038784]]),
pvalue=array([[ 4.99613833e-01, 9.65686743e-01],[ 7.89094663e-03, 1.49986458e-04]]))
————————————————
原文链接:https://blog.csdn.net/m0_37777649/article/details/74938120
2.1.5 补充:检验原理
————————————————
原文链接:https://zhuanlan.zhihu.com/p/138711532
2.2 独立样本t检验
用于检验两组服从正态分布的总体均值是否一样,前提是两个样本方差相等。如果两组样本彼此不独立,应该使用配对样本t检验。
2.2.1 目的
检验两独立样本的均值是否相等。
2.2.2 要求
两样本独立,服从正态分布或近似正态。
2.2.3 根据总体方差是否相等可以分为两类
2.2.3.1 总体方差相等且未知 样本方差满足
2.3.3.2 总体方差不等且未知(或者对它们一无所知)满足
2.3.3.3 检验原理(方差相等或不等都适用)
————————————————
原文链接:https://zhuanlan.zhihu.com/p/138711532
2.2.4 python中的独立样本T检验 ttest_ind
from scipy import stats
import numpy as np
np.random.seed(12345678)
#loc:平均值 scale:方差
rvs1 = stats.norm.rvs(loc=5,scale=10,size=500)
rvs2 = stats.norm.rvs(loc=5,scale=10,size=500)
- 当两总体方差相等时,即具有“方差齐性”,可以直接检验
- 不拒绝原假设——两总体均值相等
stats.ttest_ind(rvs1,rvs2, equal_var = True)
LeveneResult(statistic=0.9775501222315258, pvalue=0.323044034693146)
- 如果两总体具有方差齐性,错将equal_var设为False,p值变大
stats.ttest_ind(rvs1,rvs2, equal_var = False)
Ttest_indResult(statistic=0.26833823296238857, pvalue=0.78849452749501059)
- 当不确定两总体方差是否相等时,应先利用levene检验,检验两总体是否具有方差齐性。
stats.levene(rvs1, rvs2)
LeveneResult(statistic=1.0117186648494396, pvalue=0.31473525853990908)
p值远大于0.05,认为两总体具有方差齐性。
如果两总体不具有方差齐性,需要将equal_val参数设定为“False”。这里设置成False则进行Welch’s t-test而不是Student’s t-test
注:
- 两总体方差不等时,若没有将equal_var参数设定为False,则函数会默认equal_var为True,这样会低估p值
rvs3 = stats.norm.rvs(loc=5, scale=20, size=500)
stats.ttest_ind(rvs1, rvs3)
Ttest_indResult(statistic=-0.5189533606202925, pvalue=0.6039083183389862)
- 正确的P值
rvs3 = stats.norm.rvs(loc=5, scale=20, size=500)
stats.ttest_ind(rvs1, rvs3, equal_var = False)
Ttest_indResult(statistic=0.8518907349603478, pvalue=0.39455490418122585)
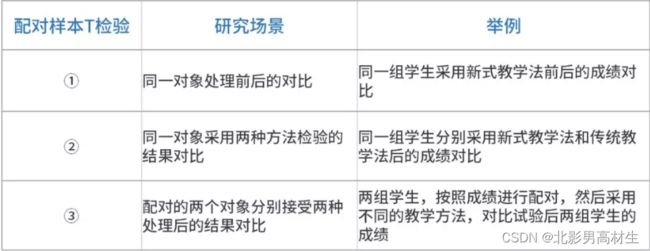
2.3、配对样本t检验
用于两个样本并不互相独立,对两个总体的均值差异进行检验,原假设d=μ1-μ2=0,即假定两个总体均值相等
2.3.1 目的
分析配对定量数据之间的差异对比关系
2.3.2 要求
- 总体方差相等
- 正态数据或近似正态
- 两个样本的样本量要相同,样本先后的顺序是一一对应的。
2.3.3 检验原理
————————————————
原文链接:https://zhuanlan.zhihu.com/p/138711532
2.3.4 python 中的配对样本T检验 ttest_rel
from scipy import stats
import numpy as np
rvs1 = stats.norm.rvs(loc=5,scale=10,size=500)
rvs2 = (stats.norm.rvs(loc=5,scale=10,size=500) + stats.norm.rvs(scale=0.2,size=500))
rvs3 = (stats.norm.rvs(loc=8,scale=10,size=500) + stats.norm.rvs(scale=0.2,size=500))
- 不拒绝原假设,认为rvs1 与 rvs2 所代表的总体均值相等
stats.ttest_rel(rvs1,rvs2)
Ttest_relResult(statistic=0.24101764965300979, pvalue=0.8096404344581155)
- 拒绝原假设,认为rvs1 与 rvs3所代表的总体均值不相等
stats.ttest_rel(rvs1,rvs3)
Ttest_relResult(statistic=-3.9995108708727924, pvalue=7.308240219166128e-05)
2.4 配对T检验与独立T检验
两者的主要区别在于:配对样本t检验需要两组样本数相等,且要求每对配对数据之间要有一定的对应关系,而独立样本t检验两组数据的样本个数可以不等
-
无论是哪种T检验,都要数据服从正态或近似正态分布。
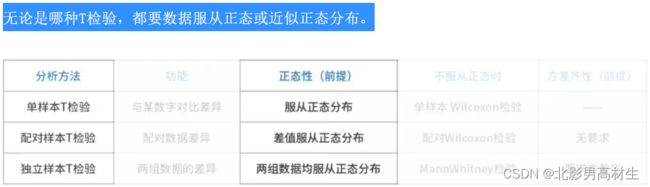
正态性有多种检验方法,常见方法如:正态图、正态性检验、P-P图/Q-Q图等。正态性检验可查看之前的文章:数据分析之正态性检验(女人近我三尺便是向我问剑)
-
非正态时处理方法
若数据满足正态性则不用考虑此步,直接选择对应方法分析。
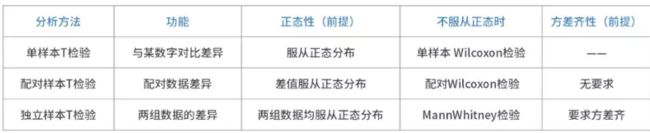
若不满足,则可考虑使用非参数检验,三种T检验对应的不同的处理方法,具体说明如下:
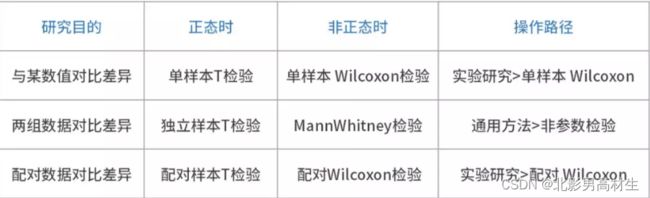
从功能上讲,它们的区别仅在于数据是否正态。除此之外,非参数检验的检验效率不如参数检验,因而在实际研究中,可能即使数据非正态,也会使用基于正态分布的参数检验。 -
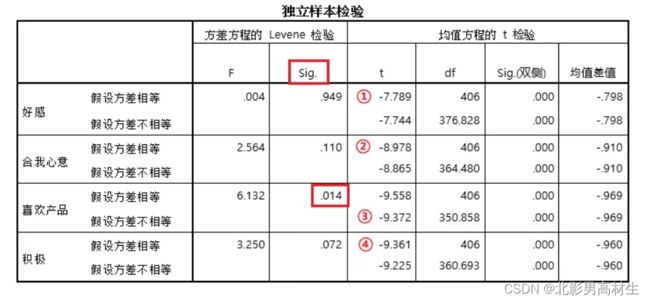
对于独立样本t检验,除了要满足正态性,还需要满足方差齐的前提条件。即方差齐的情况下,才可以使用t检验。如果方差不齐,则应采用校正T检验。
在spss软件中,会分别输出方差相等与不相等时T检验的结果,如通过Levene’s检验结果即p>0.05,则说明两组数据方差齐。
上图中只有③喜欢产品这一变量不满足方差齐条件,因此应该使用校正t检验,也就是看方差不相等时的结果。
- 无论配对t检验还是独立样本t检验,都只适用于两组数据的对比,如果数据超过两组,需要使用方差分析
参考链接:T检验分析思路完整总结,来看!
用SPSS进行T检验:
参数检验(一):为什么SPSS没有Z检验
参数检验(二):t检验的介绍与单样本t检验的SPSS操作
参数检验(三):独立样本和配对样本t检验的SPSS操作
其他T检验相关:
如何理解Z检验和T检验?
利用python进行T检验