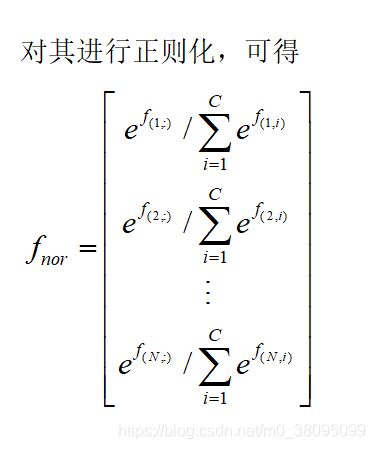
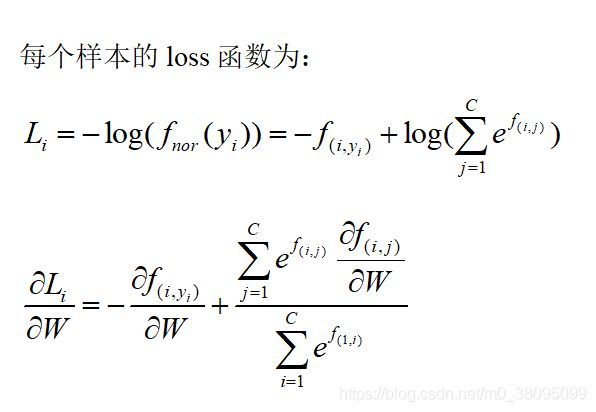cs231n_softmax损失函数对权重W求导
目录
- 前言
- 一、公式推导
-
- 1.1 将评分函数表达为矩阵形式
- 1.2 标量对列向量求导规则
- 1.3 单个样本对权重求导到全训练集
- 二、实现代码
前言
矩阵对矩阵求导法则:
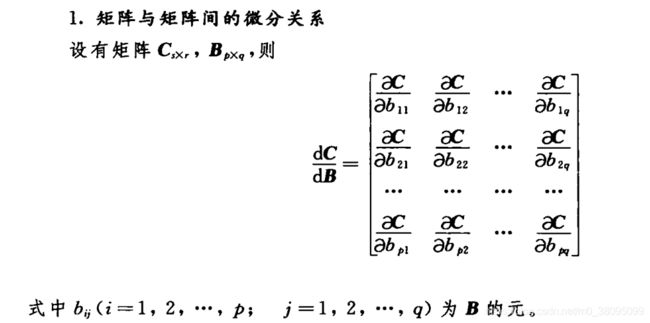
从上面公式可以看出,矩阵对矩阵求导,会导致维度倍增,即dC/dB的维度会变成(s×p,r×q),好在本文只是用到了标量(视为1*1矩阵)对矩阵求导,故所求倒数的维度和B会一样 p ∗ q p*q p∗q。
一、公式推导
基于softmax函数的损失函数形式与SVM大致一致,可直接参考。

由上面介绍可知,整个训练集的损失函数为
L = 1 N ∑ i L i + λ R ( W ) R ( W ) = ∑ k ∑ j W k , l 2 L=\frac{1}{N}\sum_{i}L_{i}+\lambda R(W)\\R(W)=\sum_{k}\sum_{j}W_{k,l}^{2} L=N1i∑Li+λR(W)R(W)=k∑j∑Wk,l2
f = X W f=XW f=XW
此处用到了和代码相同的形式,注意笔记是f=W*X,结果仅仅是转置关系,为了方便编程此处就按代码里的格式讨论了。
对于单个样本的评分函数,其公式为
L i = − f y i + l o g ( ∑ j e f j ) ∂ L i ∂ W = − ∂ f y i ∂ W + ∂ l o g ( ∑ j e f j ) ∂ W L_{i}=-f_{y_{i}}+log(\sum_{j}e^{f_{j}})\\ \frac{\partial L_{i}}{\partial W}=-\frac{\partial f_{y_i}}{\partial W}+ \frac{\partial log(\sum_{j}e^{f_{j}}) }{\partial W} Li=−fyi+log(j∑efj)∂W∂Li=−∂W∂fyi+∂W∂log(∑jefj)
1.1 将评分函数表达为矩阵形式
1.2 标量对列向量求导规则
1.3 单个样本对权重求导到全训练集

对于前两个样本,假设正确分类的标签分别是第三类和第二类,则
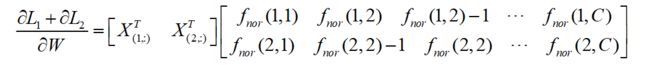
根据线性可加原则,对于所有的N个样本,有
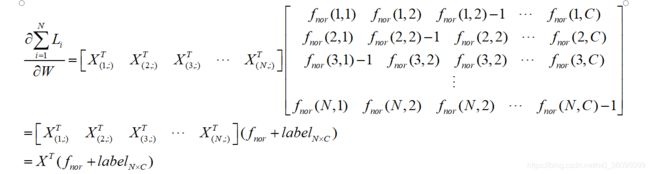
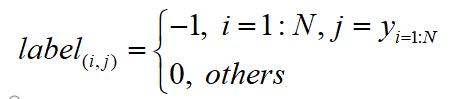
二、实现代码
代码如下(示例):
def softmax_loss_naive(W, X, y, reg):
"""
Softmax loss function, naive implementation (with loops)
Inputs have dimension D, there are C classes, and we operate on minibatches
of N examples.
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
"""
# Initialize the loss and gradient to zero.
loss = 0.0
dW = np.zeros_like(W)
N = X.shape[0]
C = W.shape[1]
for i in range(N):
score = X[i, :].dot(W)
score_exp = np.exp(score)
score_exp_nor = score_exp / np.sum(score_exp)
loss += -np.log(score_exp_nor[y[i]])
dW[:, y[i]] += - X[i]
for j in range(C):
dW[:, j] += X[i]*(np.exp(score[j]) / np.sum(score_exp))
loss = loss/N + reg * np.sum(W**2)
dW /= N
dW += 2*reg * W
矢量化实现
scores = X.dot(W)
scores_exp = np.exp(scores)
scores_exp_nor = scores_exp / ( np.sum(scores_exp, axis=1).reshape(N, 1) * np.ones([1, 10]))
loss = np.sum(-np.log(scores_exp_nor[np.arange(N), y])) / N
loss += reg*np.sum(W**2)
margin = np.zeros_like(scores)
margin += scores_exp_nor
margin[np.arange(N), y] += -1
dW = X.T.dot(margin)/N + 2 * reg * W