【人工智能】2.博弈问题、博弈搜索策略

一、问题描述方法：问题归约

1.问题归约描述

问题归约法与之前提到的状态空间法都是对进行问题描述，转换为符合或者图，但是思路不同。有许多问题可以通过一系列变换而最终变为一个子问题集合；这些子问题的解可以直接得到，通过解决这些子问题，从而就解决了初始问题。这样一种解决问题的思路就称为是问题归约法。
例如之前的汉诺塔问题，在状态空间描述中，表示的是ABC三个金片的状态 S=(i,j,k)（即位于什么位置），而在问题归约描述中，描述问题的思路是将这个复制问题拆分成几个子问题，子问题完成了，那么总的问题也就完成了。

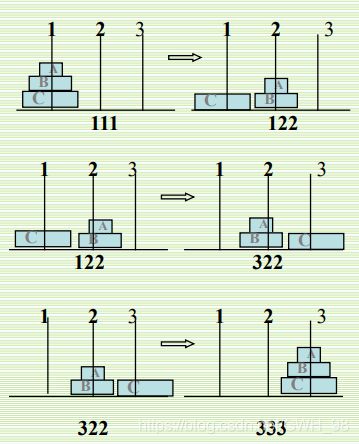
问题P：将ABC移动到3号钢针。
问题P1：把金片A及B移到2号钢针上的双金片移动问题。
问题P2：把金片C移到3号钢针上的单金片移动问题。
问题P3：把金片A及B移到3号钢针上的双金片移动问题。
与状态空间描述类似，问题归约由初始问题、问题变换操作符、本原问题组成。

2.与或图表示

1）与图：其实上面汉诺塔问题的分解就是与图。把一个问题分解成若干个问题，就可以用与图表示，只有子问题全部得到解决，原问题才能解决。P是一个与节点。

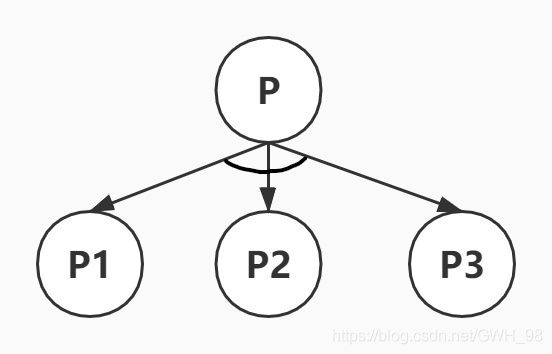
2）或图：把一个问题变换为若干个子问题，可以表示成或图。只要有一个可以解决，原问题P就可以解决，P是一个或节点。

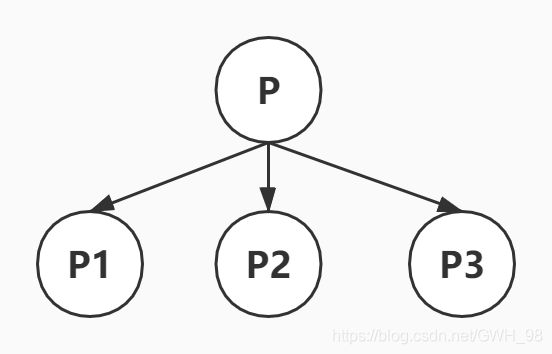
3）与或图：原问题需要通过分解和变换操作，得到本原问题，这样的归约过程可用一个与或图表示。
4）端节点：没有子节点的节点。
终叶（止）节点：本原问题所对应的节点。
可解节点：终止节点；至少有一个可解子节点的或节点；子节点全部可解的与节点。不可解节点反之。
解图（解树）：由可解节点构成的，并且由这些可解节点可以推出初始节点为可解节点的子图为解图。

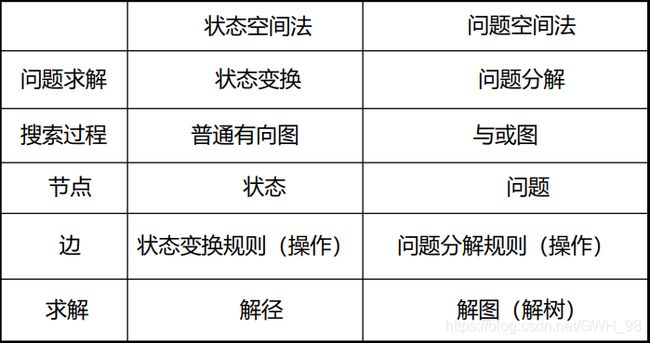
3.问题求解的比较

*在特殊情况下，只有或节点的与或图即变成普通图的状态空间搜索。

二、与或树的搜索

与状态空间搜索过程不同，因为与或树搜索出来的是一个解树，所以要不停的进行可解标示过程和不可解标示过程，自下而上进行标识：
（1）把原始问题作为初始节点S0，并把它作为当前节点；
（2）应用分解或等价变换操作对当前节点进行扩展；
（3）为每个子节点设置指向父节点的指针；
（4）选择合适的子节点作为当前节点，反复执行第（2）步和第（3）步，在此期间需要多次调用可解标记过程或不可解标记过程，直到初始节点被标记为可解节点或不可解节点为止。

1.盲目搜索

广度深度搜索，区别仅是扩展子节点在OPEN表中的顺序。搜索过程如下：
（1）把初始节点S0 放人Open表中；
（2）把Open表的第一个节点取出放入Closed表，并记该节点为n；
（3）如果节点n可扩展，则做下列工作：
① 扩展节点n，将其子节点放入Open表的尾部，并为每一个子节点设置指向父节点的指针；
② 考察这些子节点中是否有终止节点。若有，则标记这些终止节点为可解节点，并用可解标记过程对其父节点及先辈节点中的可解节点进行标记。如果初始解节点S0能够被标记为可解节点，就得到了解树，搜索成功，退出搜索过程；如果不能确定S0为可解节点，则从Open表中删去具有可解先辈的节点；
③ 转第（2）步。
（4）如果节点n不可扩展，则做下列工作：
① 标记节点n为不可解节点；
② 应用不可解标记过程对节点n的先辈中不可解的节点进行标记。如果初始解节点S0也被标记为不可解节点，则搜索失败，表明原始问题无解，退出搜索过程；如果不能确定S0为不可解节点，则从Open表中删去具有不可解先辈的节点；
③转第（2）步。

2.启发式搜索

1）与或树的启发式搜索时寻求最优解树的过程，即代价最小的解树。
2）节点的代价怎么定义和计算：
① 如果n为终止节点：
h(n)=0
② 如果n为或节点，且子节点为n1，n2，…，nk：
h(n)= min {c(n，ni)＋ h(ni)} (1≤i≤k)
③ 如果n为与节点，且子节点为n1，n2，…，nk：
和代价法： h(n)= ∑((c(n，ni)＋ h(ni)) i=1,2,……,k
最大代价法： h(n)= max{c(n，ni)＋h(ni)} (1≤i≤k)
④ 如果n是端节点，但又不是终止节点：
h(n)= ∞
按这种计算方法，最后得到的解树的代价累加到初始节点上，即为初始节点的代价。
3）希望树的概念：
在启发式的最优解树求解过程中，任何时刻都应该选择那些最有希望成为最优解树一部分的节点进行扩展，随着求解过程中不断扩展，要对希望值进行不断地估计和修正。
4）搜索过程：自顶向下，图生成过程 扩展节点，从希望树中选择一个节点扩展；自底向上，计算代价过程 修正代价估值，重新选择希望树。
(1) 把初始节点S0放入Open表中，计算h(S0)；
(2) 计算希望树T；
(3) 依次在Open表中取出T的端节点放入Closed表，并记该节点为n；
(4) 如果节点n为终止节点，则做下列工作：
① 标记节点n为可解节点；
② 在T上应用可解标记过程，对n的先辈节点中的所有可解解节点进行标记；
③ 如果初始解节点S0能够被标记为可解节点，则T就是最优解树，成功退出；
④ 否则，从Open表中删去具有可解先辈的所有节点。
⑤ 转第(2)步。
(5) 如果节点n不是终止节点，但可扩展，则做下列工作：
① 扩展节点n，生成n的所有子节点；
② 把这些子节点都放入Open表中，并为每一个子节点设置指向父节点n的指针
③ 计算这些子节点及其先辈节点的h值；
④ 转第(2)步。
(6) 如果节点n不是终止节点，且不可扩展，则做下列工作：
① 标记节点n为不可解节点；
② 在T上应用不可解标记过程，对n的先辈节点中的所有不可解解节点进行标记；
③ 如果初始解节点S0能够被标记为不可解节点，则问题无解，失败退出；
④ 否则，从Open表中删去具有不可解先辈的所有节点。
⑤ 转第(2)步。

三、博弈树的启发式搜索

1.什么是博弈树

1）研究的是一类：二人零和、全信息、非偶然的博弈
二人零和：一方赢，另一方输；或者平局
全信息：知道当前和历史
非偶然：任何一方走步时，都选择对自己最为有利，而对另一方最为不利的行动方案
2）在博弈树中：
①博弈的初始状态是初始节点；
②博弈树中的“或”节点和“与”节点是逐层交替出现的；（我方每次下是或，我方只有一种选择走；对手每次下是与，要估计对手全部的选择可能是哪些）
③整个博弈过程始终站在某一方的立场上，所有能使自己一方
获胜的终局都是本原问题，相应的节点是可解节点；所有使对方获胜的终局都是不可解节点。

2.极大极小分析

1）为其中一方选择最优行动方法；
2）要考虑每一方案实施后对方所要采取的行动，并计算可能的得分；
3）根据问题的特性信息定义评价函数（我方的得分）；
4）端节点的估值计算出后，再推算出父节点的得分。
或节点，选择子节点中最大得分（MAX）作为父节点的得分；（我方下对我方最有利的）
与节点，选择子节点中最小得分（MIN）作为父节点的得分；（对方下对我方最利的）
解树的得分越大越有利，对于很多要走很多步的解，通常不会进行全局的搜索，而是只在局部搜索局部的最优解，指导本次如何移动。

3. $\alpha$-$\beta$剪枝分析

对于$\alpha$-$\beta$剪枝死记硬背不好用，理解之后自然就明白了。
1）$\alpha$值：或节点：子节点中的最大倒推值的下界；$\beta$值：与节点：子节点中的最小倒推值的上界。
2）$\alpha$剪枝：若任一极小层节点 m 的$\beta$值小于或等于其位于极大层的父节点的$\alpha$值，则可终止该极小层中节点 m 以下的搜索过程。

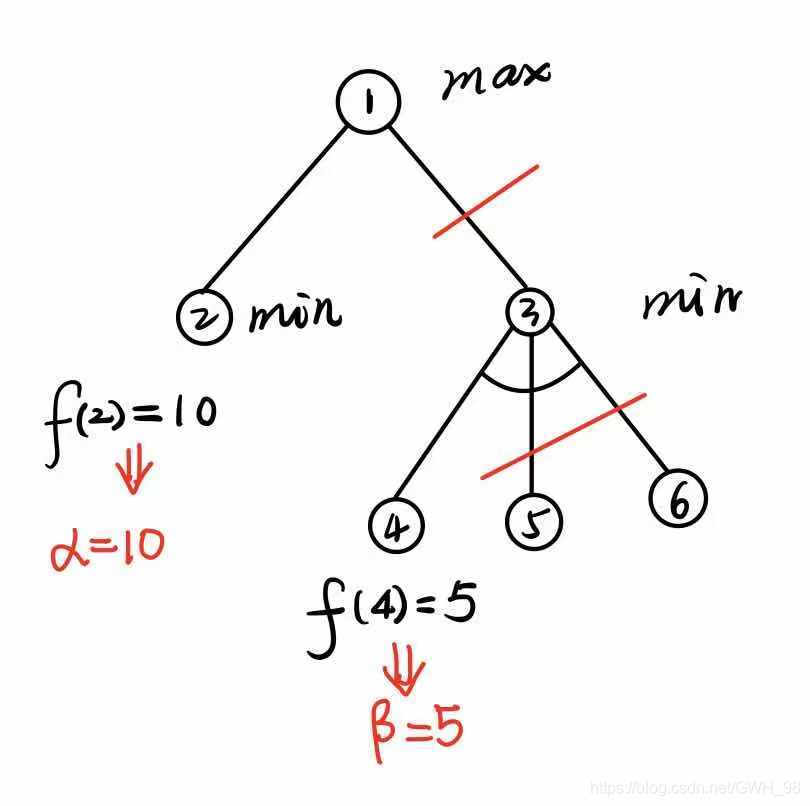
  $\beta$剪枝：若任一极大层节点 m 的$\alpha$值大于或等于其位于极小层的父节点的$\beta$值，则可终止该极大层中节点 m以下的搜索过程。

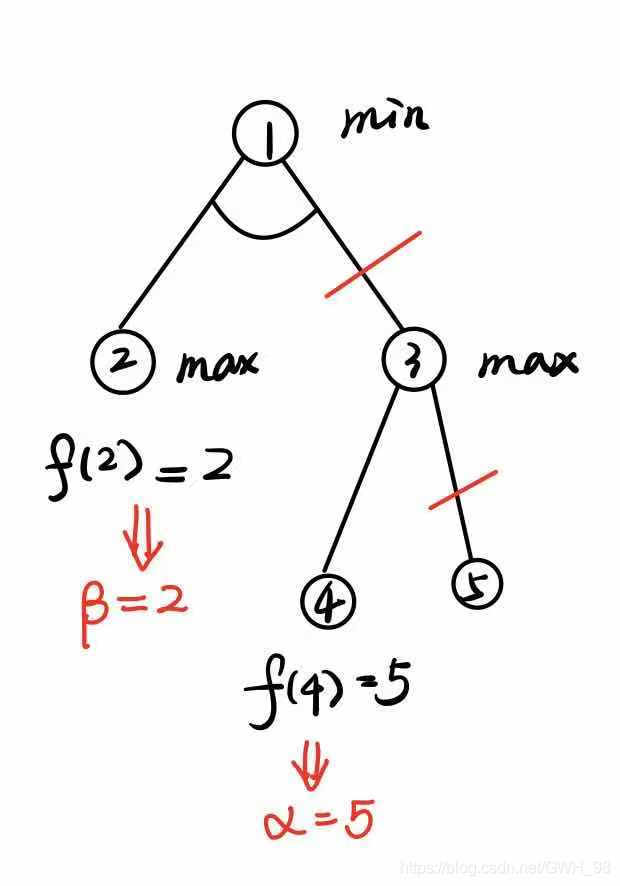
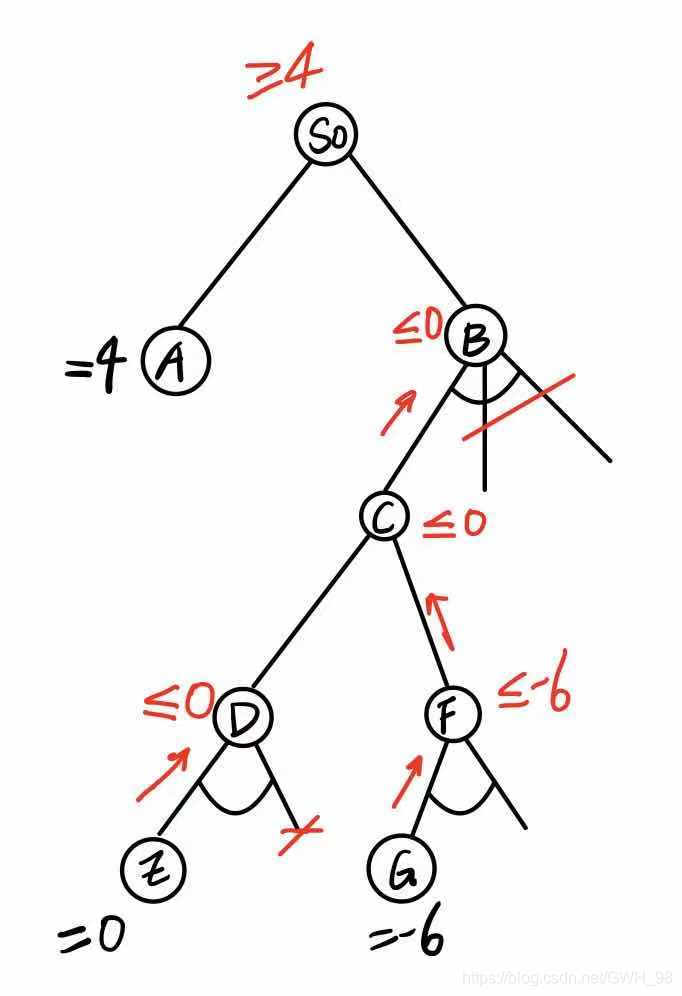
3)注意：要进行$\alpha$-$\beta$剪枝,至少必须使某一部分的搜索树生长到最大深度；采用$\alpha$-$\beta$过程都要使用某种深度优先的搜索方法；比较都是在极小结点和极大结点间进行的；$\alpha$$\beta$的影响可以是隔层的，例如：
如下图，已知扩展到A=4，继续扩展B，扩展到E时，E=0就可以自下而上推，对于C有两种可能，无论是取D<=0，导致B<=0；还是取F，D的第二个子节点都不需要再扩展了，相当于这个节点对于S0的增大已经没有贡献了，但是如果，E>=5的情况就不一样了。

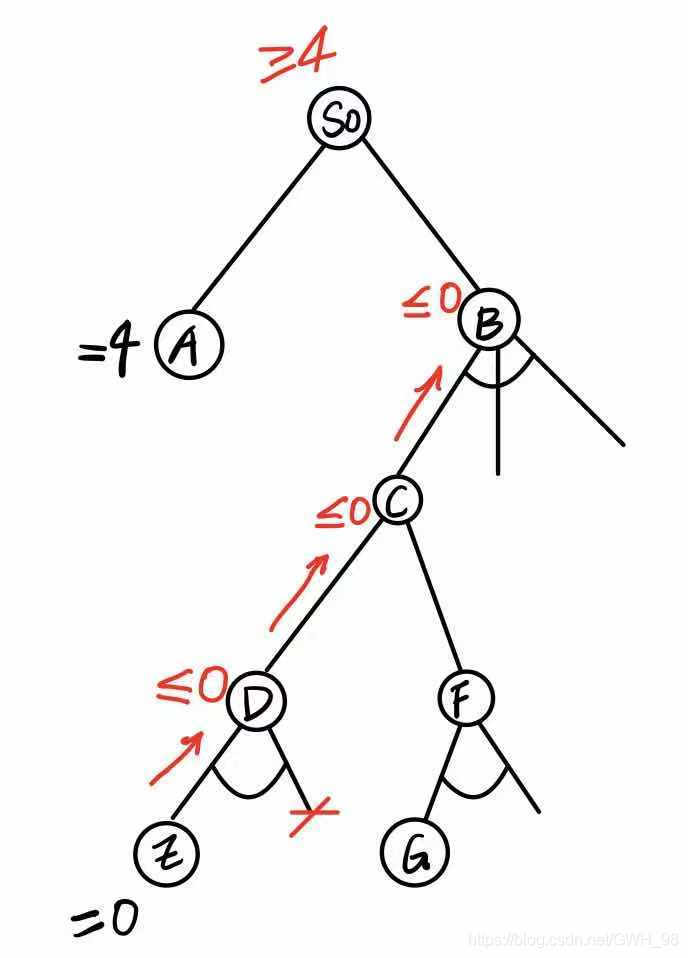
再继续如下图，对于G如果为-6，同样可以推出，G的兄弟节点不需要再扩展了。这种隔层剪枝的情况发生再隔层的$\alpha$$\beta$值之间