数据结构 | 顺序栈与链式队【栈与队列的交际舞】
数据结构之栈与队列
- 顺序栈
-
- 前言
-
- 栈的结构简介及概述
- 为什么要用顺序栈?
- 结构声明
- 接口算法实现
-
- 初始化栈
- 销毁栈
- 入栈
- 出栈
- 返回栈顶元素
- 判空
- 栈的元素个数
- ⭐开发思维 :一切功能均封装
- 运行测试
-
- 生活小案例:故障的ATM取款机&过万的打车费
- 整体代码展示
- 链式队
-
- 前言
-
- 队列的结构简介及概述
- 为什么要用链式队?
- 结构声明
- 接口算法实现
-
- 初始化队列
- 销毁队列
- 入队
- 出队
- 获取队头
- 获取队尾
- 判空
- 求解队列大小
- 运行测试
- 整体代码展示
- OJ题目实训
-
- ⌨【LeetCode】225.用队列实现栈
- ⌨【LeetCode】232.用栈实现队列
- ⌨【LeetCode】622.设计环形队列
- 栈与队列的实际应用
-
- 后缀表达式——栈
- 浏览器的前进后退——栈
- 业务办理系统——队列
- 迷宫问题——栈与队列
- 总结与提炼
顺序栈
前言
栈的结构简介及概述
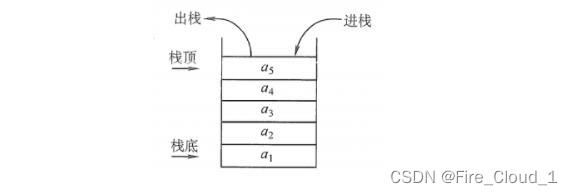
首先我们要来讲的一种数据结构叫做【栈】,相信你一定不陌生,在很多场合都听说过,以及在代码出Bug时都会有【栈溢出】这样一种错误发生,但那种栈是内存中的栈,和我们数据结构中的栈可不一样。接下来我们一起来看看这种数据结构
- 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端
称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 - 【压栈】:栈的插入操作叫做进栈/压栈/入栈,入数据在栈顶。
- 【出栈】:栈的删除操作叫做出栈。出数据也在栈顶。
为什么要用顺序栈?
- 那对于栈,为什么标题我写的是顺序栈呢,相信在学校的教材中,大家应该都接触过链式栈,就是使用我们前面所学过的单链表来进行一个模拟,我们在学习单链表的时候知道,对于很多场合,链表比顺序表来的更加受欢迎,因为其对于结点的插入和删除非常的方便
- 那有同学就会疑问,对于栈的实现,为什么不用链式栈呢,听起来也比较酷一些。我们通过图解来分析一下
- 对于顺序表来说,尾插尾删效率高一些,头插头删需要移动数据,因此将数组首元素所在位置作为栈底,尾元素所在位置作为栈顶,负责出入数据
- 对于链表来说,头插头删效率高一些,尾插尾删需要考虑是否更改头结点,因此将链表头作为栈顶,链表尾作为栈底
所以我选择使用顺序栈来实现,因为其实现起来比较简单、快捷;当前链式栈也是可以的
结构声明
- 首先我们来看看其结构。可以看到,虽然我使用的是顺序栈,但确是动态的顺序栈,也就是我们顺序表中所讲到过的动态扩容机制,这很好地弥补了因为数组大小定死而带来的困惑
typedef int STDataType;
typedef struct Stack {
STDataType* a;
int top; //栈顶指针
int capacity; //容量
}ST;
接口算法实现
接下去是对于顺序栈的接口算法实现
初始化栈
- 首先,我们可以在初始化的时候就动态开辟出来这个数组,在顺序表中我们是在插入的时候容量不够实现的扩容机制中使用【realloc】来进行的一个复用,在顺序栈中的话我们直接在初始化的时候就先开辟出一块空间也可
void InitStack(ST* st)
assert(st); //警惕随意操作,传入空指针
st->a = (STDataType*)malloc(sizeof(STDataType) * 4);
if (st->a == NULL)
{
perror("fail mallic");
exit(-1);
}
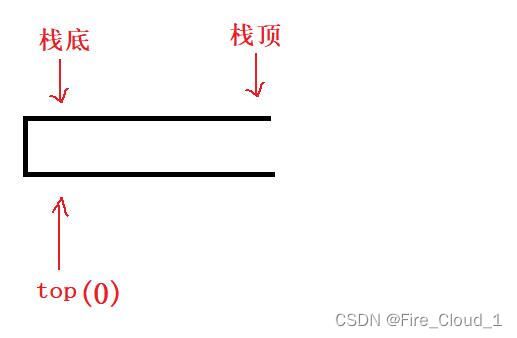
- 然后对结构体内的成员初始化。比较重要的就是这个【top】栈顶指针的初始化,我这里将其初始化为0,当然你也可以将其初始化为-1,不过其他接口的算法是需要做一个调整的,这一块我们在【入栈】的时候做讲解
st->top = 0; //初始化为0表示指向当前栈顶元素的后一元素
st->capacity = 4;
销毁栈
- 申请了一块空间,那自然要对其进行一个释放
void DestroyStack(ST* st)
{
assert(st);
free(st->a);
st->a = NULL;
st->top = st->capacity = 0;
}
入栈
- 好,接下去我们来说说最重要的一块,就是【入栈】这个基本操作,也就是要使用到栈顶指针【top】
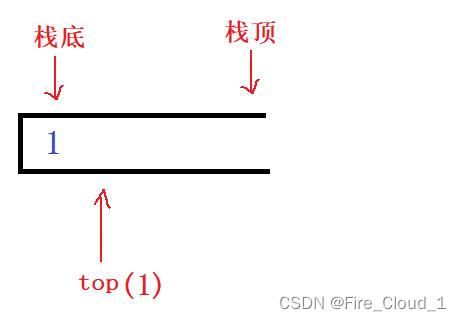
- 我们首先来细聊一下有关这个栈顶指针【top】的使用,首先可以看到,在初始化的时候我们将【top】是置于一个0的位置,这其实也就是需要放入第一个数据的位置,那么直接执行下面这个语即可
st->a[st->top] = x; //top指向栈顶元素的后一元素,因此直接入栈即可
- 但是在入栈完第一个数据后我们还要在后面入下一个数据,因为将【top++】
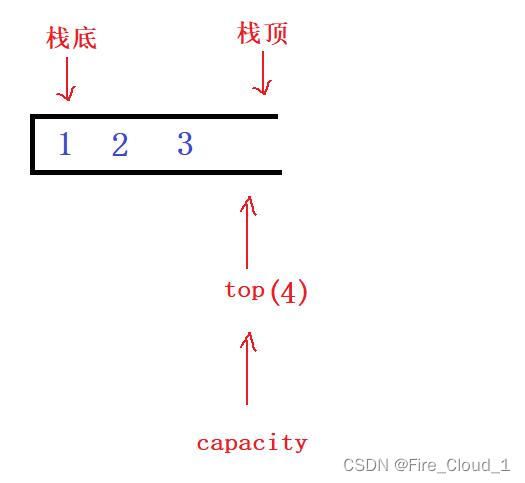
- 但是当这个栈顶指针向后偏移的时候,当此时入栈完这个数据3,执行【top++】,那此时的【top == capacity】,也就是等于这个栈的容量。
- 接着你就需要去进行一个联想,若是继续入栈一个数据后栈顶指针继续++,就会超过这个栈的容量,那此时就成了【数组访问越界】,从而导致一个经典的【栈溢出】。此时相信很多同学对这样的情况已经是非常敏锐了,没错,接下去就需要进行扩容了
- 可以看到代码,和我们顺序表的一个扩容机制很相似,但是在顺序表中我们多进行了一个三目运算符的判断,也就是当这个顺序表的容量为0的时候,也就相当于是第一次入栈数据时,下面在执行realloc就相当于是malloc,这个我在顺序表中也有讲到过
- 但是在顺序栈中,我早已埋下伏笔,在初始化的时候就为这个栈开辟一块大小为4的空间,这样在栈满需要扩容的时候就无需进行额外的判断了,这个看个人喜好,都可以
//栈满扩容逻辑
if (st->top == st->capacity)
{
//初始化时已经malloc开辟过空间了,因此无需考虑容量为空的情况
STDataType* tmp = (STDataType*)realloc(st->a, st->capacity * 2 * sizeof(STDataType));
if (tmp == NULL)
{
perror("fail realloc");
exit(-1);
}
st->a = tmp;
st->capacity *= 2;
- 你可以上下去进行一个对比,----》顺序表
//顺序表扩容逻辑
void SLCheckCapacity(SL* ps)
{
//扩容
/* 酒店的案例
* 原地扩容:发现与上一次开辟空间旁有足够的位置
* 异地扩容:没有足够的位置,重新找一块地方,将原来开辟空间中的内容自动拷贝过来放在新空间中
* 然后释放原来的空间
*/
if (ps->size == ps->capacity)
{
int newCapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;
SLDataType* tmp = (SLDataType*)realloc(ps->a, newCapacity * sizeof(SLDataType*));
//判断是否开辟空间成功【失败会返回空指针null pointer】
if (tmp == NULL)
{
perror("realloc fail\n");
exit(-1); //结束掉程序【程序异常结束】
}
//扩容成功
ps->a = tmp;
ps->capacity = newCapacity;
}
}
出栈
- 有出栈,那一定有入栈,对于出栈非常直观,就是【top–】
- 但是你在减减这个top的时候一定要注意,因为在不断地退栈过程中栈顶指针就会到达栈底,若是再向下,这个时候其实就不对了,我们在顺序表中的尾删也讲到过,对于栈的话就需要去考虑会不会向下越界
- 因此需要去判断这个栈顶指针是否为我们初始化时的0
if(top == 0)
return;
- 之前说过,这样太温柔了,要暴力一点,直接断言。Empty()在后面会讲到
assert(!StackEmpty(st)); //用Empty去判断无需考虑栈顶指针Top
返回栈顶元素
- 接下去是取栈顶元素,因为我们初始化时间的top为0,指向当前栈顶元素的下一个位置,所以在取栈顶元素的时候就需要让【top - 1】
return st->a[st->top - 1];
- 下面是两个栈顶指针初始化不同时的返回结果,这一块很重要❗❗❗要搞懂
判空
- 然后便是我们上面所说到的Empty()判空,很简单,判断一下栈顶指针即可
bool StackEmpty(ST* st)
{
return (st->top == 0); //看初始化时的栈顶指针top
}
栈的元素个数
- 最后一个接口就是返回当前栈有多少元素,因为我们的栈顶指针是指向当前元素的下一个位置,根据下标为0来看,刚好就是元素的个数;若是你top初始化为-1,那么当你需要返回栈顶元素的时候,当前栈顶指针top便指向当前的栈顶元素,所以元素个数便是【top - 1】
int StackSize(ST* st)
{
return st->top;
}
⭐开发思维 :一切功能均封装
其实讲到这个接口的算法实现就有小伙伴提出疑问了,栈顶指针的逻辑我是搞懂了,但是就这样一个求解栈元素个数的功能,为什么不直接在使用的时候获取呢?而是要单独封装为一个函数?这其实就是你缺乏工程经验了
- 为什么会我将这么一个简单的功能都封装为函数呢,这个其实我在C语言函数那块就有讲到,凡是我们遇到一个需要反复使用的功能,那最好的办法就是将其封装为函数,可以进行直接调用,这个反复使用值得不是我们在单独测试的时候调用,而是你写出来这个栈要放到实际的工程中,别人就可能会多次调用你的这个API,以及我们后面有一道OJ题目就要很频繁地使用到这个Size()
- 还有一点其实就方便了调用这个功能的人,因为它不需要去考虑这个函数的内部实现是怎样的,只需要去调用即可,但若是我们直接去获取这个【top】,刚才我说过了,可能这个栈的实现者在初始化的时候将top置为-1,那么此时我们就需要获取【top - 1】的位置,这就会让调用这个API的人感觉到很麻烦
- 不仅仅是对于这个Size()来说,Empty()也是一样,你怎么知道这个【top】指向何处时栈为空呢,但如是你拥有一个这样的API,就无需考虑其内部实现细节
现在你应该知道为什么要将这个求解Size的功能以及Empty()单独封装为一个函数了吧
运行测试
实现完了这个栈的接口算法,接下来我们来测试一波~
生活小案例:故障的ATM取款机&过万的打车费
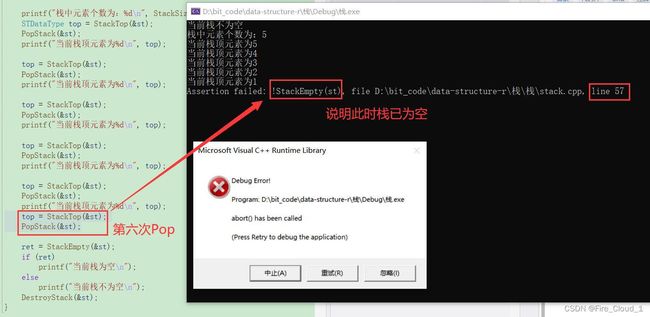
- 可以看到,是没有问题的,但是我这里要给你测试一下多Pop()一次会怎样,也就是当这个栈中元素都出完以后再去进行一个【出栈操作】,可以看到,因为我们在出栈的时候进行了一个判空操作,因此程序直接报出了Error
- 根据这一块我讲一个生活中的小案例,帮助大家理解,也可以轻松一刻
- 这个时候你去出栈,但是明明栈中没有元素了,但还是要再去取一下其实就对应你去ATM机取钱一样,明明知道自己卡里没有钱了,但是还要去取一下试试看,想着万一没有余额了再去取万一能够取出来就可以发大财了,一般钱不会是负数,于是被系统当成了无符号整数【unsigned int】,于是突出给出来几千万的数目,你拿到钱之后就一顿大吃大喝
- 我们平常在赶不及的时候都会选择去打车,一般滴滴打车用的比较多,但如是有一天这个计费的屏幕突然出来一个过万的数字,那你是不会吓死了,这个时候其实就是内部的程序出Bug了,内部执行的数据被当成了一个无符号整数执行,因此就会出现这么大的数字。
- 所以大家平常在写代码的时候一定要考虑地周全一些
整体代码展示
stack.h
#pragma once
#include stack.cpp
#define _CRT_SECURE_NO_WARNINGS 1
//顺序表尾插尾删快、头插头删慢(需要移动数据)
//链表头插头删快、尾插尾删慢(需要考虑头结点是否改变)
//--->因此栈选择使用数组的形式实现,不用链式栈
#include "stack.h"
/*初始化栈*/
void InitStack(ST* st)
{
assert(st); //警惕随意操作,传入空指针
st->a = (STDataType*)malloc(sizeof(STDataType) * 4);
if (st->a == NULL)
{
perror("fail mallic");
exit(-1);
}
st->top = 0; //初始化为0表示指向当前栈顶元素的后一元素
st->capacity = 4;
}
/*销毁栈*/
void DestroyStack(ST* st)
{
assert(st);
free(st->a);
st->a = NULL;
st->top = st->capacity = 0;
}
/*入栈*/
void PushStack(ST* st, STDataType x)
{
//栈满扩容逻辑
if (st->top == st->capacity)
{
//初始化时已经malloc开辟过空间了,因此无需考虑容量为空的情况
STDataType* tmp = (STDataType*)realloc(st->a, st->capacity * 2 * sizeof(STDataType));
if (tmp == NULL)
{
perror("fail realloc");
exit(-1);
}
st->a = tmp;
st->capacity *= 2;
}
st->a[st->top] = x; //top指向栈顶元素的后一元素,因此直接入栈即可
st->top++; //然后栈顶指针后移,为下一次入栈做准备
}
/*出栈*/
void PopStack(ST* st)
{
assert(st);
//assert(st->top > 0);
assert(!StackEmpty(st)); //用Empty去判断无需考虑栈顶指针Top
st->top--;
}
/*返回栈顶元素*/
STDataType StackTop(ST* st)
{
return st->a[st->top - 1];
}
/*判空*/
bool StackEmpty(ST* st)
{
return (st->top == 0); //看初始化时的栈顶指针top
}
/*栈的元素个数*/
int StackSize(ST* st)
{
return st->top;
}
test.cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include "stack.h"
void StackTest1()
{
ST st;
InitStack(&st);
PushStack(&st, 1);
PushStack(&st, 2);
PushStack(&st, 3);
PushStack(&st, 4);
PushStack(&st, 5);
bool ret = StackEmpty(&st);
if (ret)
printf("当前栈为空\n");
else
printf("当前栈不为空\n");
printf("栈中元素个数为:%d\n", StackSize(&st));
STDataType top = StackTop(&st);
PopStack(&st);
printf("当前栈顶元素为%d\n", top);
top = StackTop(&st);
PopStack(&st);
printf("当前栈顶元素为%d\n", top);
top = StackTop(&st);
PopStack(&st);
printf("当前栈顶元素为%d\n", top);
top = StackTop(&st);
PopStack(&st);
printf("当前栈顶元素为%d\n", top);
top = StackTop(&st);
PopStack(&st);
printf("当前栈顶元素为%d\n", top);
top = StackTop(&st);
PopStack(&st);
ret = StackEmpty(&st);
if (ret)
printf("当前栈为空\n");
else
printf("当前栈不为空\n");
DestroyStack(&st);
}
int main(void)
{
StackTest1();
return 0;
}
链式队
前言
说完栈之后,我们就该来说说队列了,对于队列,我是使用链表实现的
队列的结构简介及概述
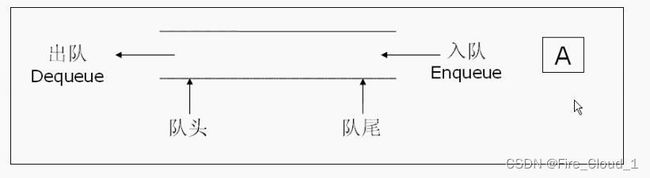
- 队列:只允许在一端进行插入数据操作,在另一端进行删除数据操作的特殊线性表,队列具有先进先出
FIFO(First In First Out) 入队列:进行插入操作的一端称为队尾 出队列:进行删除操作的一端称为队头
为什么要用链式队?
- 对于栈我使用的是顺序栈,这个你应该已经非常清楚为什么了,但是对于队列,为什么我是用的是链式队呢,我们还是通过画图来分析一下
- 对于顺序队来说,若是我们将其末尾当做队尾,将其起始当做队头,那么在进行出队的时候就要移动整体的元素,这其实也就是顺序表的一大缺陷,所以实现起来效率会大打折扣
- 对于链式队来说,我们将其初始当做队头,那么对于单链表来说,删除头结点的效率非常高,只是在入队的时候需要做一个头是否为空的判断
所以我选择使用链式队来实现,因为其实现起来比顺序队来的高效、可靠;
结构声明
- 接着一样来看看其结构声明,对于链式队的结构有所不同,我们需要封装两个结构体,一个是队列中的结点,一个则是封装队头指针和队尾指针
typedef int QDataType;
typedef struct QueueNode {
QDataType data;
struct QueueNode* next;
}QNode;
typedef struct Queue {
QNode* front;
QNode* rear;
size_t sz;
}Qu;
接口算法实现
接下去是对于链式队的接口算法实现
初始化队列
- 初始很简单,无需开辟空间,直接对队列的头尾指针以及sz进行一个初始化即可
void QueueInit(Qu* q)
{
q->front = NULL;
q->rear = NULL;
q->sz = 0;
}
销毁队列
- 对于销毁队列,其实也就是我们销毁单链表的过程。你可能已经忘了,我们再看一遍吧
void SLIstDestroy(SLTNode** pphead)
{
SLTNode* cur = *pphead;
while (cur)
{
SLTNode* nextNode = cur->next;
free(cur);
cur = nextNode;
}
*pphead = NULL;
}
- 可以看到,对于单链表而言就是从首结点开始一一往后进行一个删除操作,其实对于队列也是一样的,不过它有一个队头指针和队尾指针,我们可以先定义一个指向结点的指针变量,让其指向与【front】一同的方向,换一种思路,首先保存下一个结点,然后删除当前指针所指向的结点即可
- 这里被释放后的结点置不置空都可以,因为它是一个局部变量,它的改变不会引起外部链表的结构变化,这个我在单链表也详细介绍过
QNode* cur = q->front;
while (cur)
{
QNode* del = cur;
cur = cur->next;
free(del);
//del = NULL; 无需再将del置为空,因为其为局部变量不会被访问到
}
- 但是在最后的话别忘了将这个队头指针和队尾指针置为空,否则若是链队结点都被你释放了,但是这两个指针却还指向它们,这就变成了【野指针】
- 不过你使用我的代码去调试一下可以发现,不加这句话【front】和【rear】也是会被置空的,这是因为我在出队的时候做了单个结点的判断,继续看下去吧
入队
- 接着来讲讲入队操作,首先很简单,去堆区申请一块空间来初始化构建一个结点
/*创建结点初始化*/
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode == NULL)
{
perror("fail malloc");
exit(-1);
}
newNode->data = x;
newNode->next = NULL;
- 接下去的话就是一个入队的操作了,因为是从队尾入队,所以相当于是一个尾插的操作,分别去进行一个判断即可
/*尾插*/
if (q->rear == NULL)
{ //队列为空
q->front = q->rear = newNode;
}
else
{
q->rear->next = newNode;
q->rear = newNode;
}
出队
- 马上,我们来到出队的操作,对于出队,我在上面也有提到过,就是单个结点需要单独判断,首先我们来看看多个结点的删除。也是一样很简单的删除逻辑
//有多个结点
QNode* del = q->front;
q->front = q->front->next;
free(del);
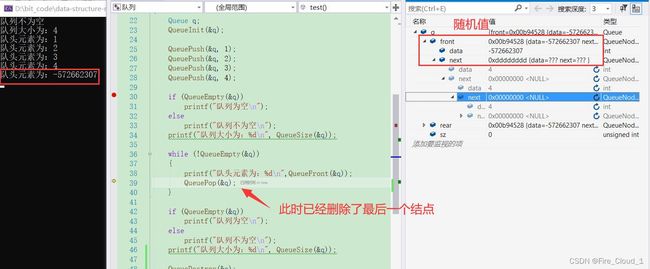
- 但是光写这个是不够的,因为当你出队得只剩一个结点时【q->front->next】访问的便是一个空指针,因此我们需要单独去做一个判断
- 可以看到,我将最后一个结点释放了之后又将首尾指针也置为空
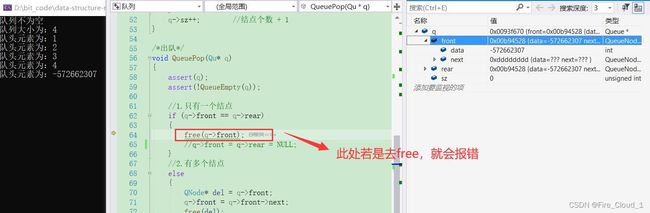
//只有一个结点
if (q->front == q->rear)
{
free(q->front);
q->front = q->rear = NULL;
}
- 所以大家在处理最后单个结点的时候一定要考虑仔细了
- 获取队头和队尾结点很简单,【return data】即可,但是要注意判断,若是链队已为空就不可以去访问
获取队头
QDataType QueueFront(Qu* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->front->data;
}
获取队尾
QDataType QueueBack(Qu* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->rear->data;
}
判空
- 判空的话也就是当队头指针和队尾指针都为空时,即释放完最后一个结点的那一刻这个链队就空了
bool QueueEmpty(Qu* q)
{
assert(q);
return q->front == NULL && q->rear == NULL;
}
求解队列大小
- 终于是说到这里了,相信很多小伙伴对于我 在封装队头和队尾指针时非常异或为什么要去再加入一个【sz】去保存它的大小,这里在求解大小的时候就会用到
- 试想我们在单链表中求解结点个数的时候是不是使用到了循环去求解,分析一下就可以知道那是一个O(N)的时间复杂度,但是看我上面实现的这个接口算法,都是O(1)的时候复杂度,这里突然出现个O(N),那不是破坏阵型了
- 而且我在栈的时候也说过这个Size()在实际中可能会被频繁调用,而且很可能是放在一个循环里调的,这就无形之中成了O(N2)的复杂度。所以我使用【空间换时间】的思路,直接在结构体中记录这个变量,然后每次在【Push】和【Pop】的时候更新一个这个【sz】即可
size_t QueueSize(Qu* q)
{
return q->sz;
}
Push
sz++;
Pop
sz--;
- 看完了上面的接口算法实现,相信你对链式队也有了一个基本的认识,是不是感觉很简单,并没有链表那么复杂
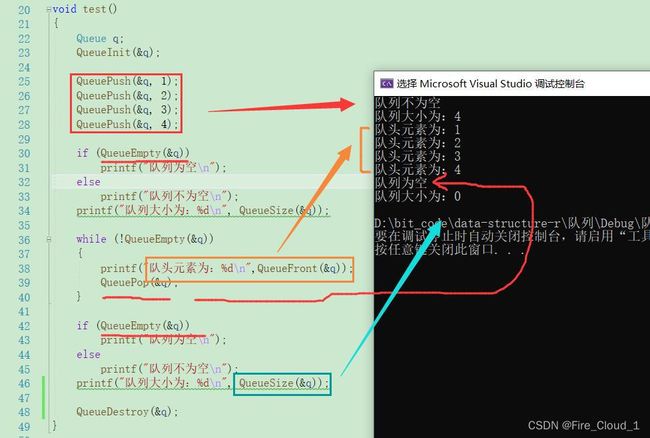
运行测试
接下来我们继续来测试一波~
整体代码展示
queue.h
#pragma once
#include queue.cpp
#define _CRT_SECURE_NO_WARNINGS 1
#include "queue.h"
/*初始化队列*/
void QueueInit(Qu* q)
{
q->front = NULL;
q->rear = NULL;
q->sz = 0;
}
/*销毁队列*/
void QueueDestroy(Qu* q)
{
assert(q);
QNode* cur = q->front;
while (cur)
{
QNode* del = cur;
cur = cur->next;
free(del);
//del = NULL; 无需再将del置为空,因为其为局部变量不会被访问到
}
q->front = q->rear = NULL; //头尾指针要置空
}
/*入队*/
void QueuePush(Qu* q, QDataType x)
{
assert(q);
/*创建结点初始化*/
QNode* newNode = (QNode*)malloc(sizeof(QNode));
if (newNode == NULL)
{
perror("fail malloc");
exit(-1);
}
newNode->data = x;
newNode->next = NULL;
/*尾插*/
if (q->rear == NULL)
{ //队列为空
q->front = q->rear = newNode;
}
else
{
q->rear->next = newNode;
q->rear = newNode;
}
q->sz++; //结点个数 + 1
}
/*出队*/
void QueuePop(Qu* q)
{
assert(q);
assert(!QueueEmpty(q));
//1.只有一个结点
if (q->front == q->rear)
{
free(q->front);
q->front = q->rear = NULL;
}
//2.有多个结点
else
{
QNode* del = q->front;
q->front = q->front->next;
free(del);
}
q->sz--;
}
/*获取队头*/
QDataType QueueFront(Qu* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->front->data;
}
/*获取队尾*/
QDataType QueueBack(Qu* q)
{
assert(q);
assert(!QueueEmpty(q));
return q->rear->data;
}
/*判空*/
bool QueueEmpty(Qu* q)
{
assert(q);
return q->front == NULL && q->rear == NULL;
}
/*求解队列大小*/
size_t QueueSize(Qu* q)
{
return q->sz;
}
test.cpp
#define _CRT_SECURE_NO_WARNINGS 1
//顺序队 —— 需要在队头出入数据很麻烦
//--->链队
/*
* 1.单
* 2.哨兵位 可要可不要
* 3.非循环
*/
/* 若指针指向一块空间释放了,需不需要置空?
* 若是别人能访问到,就需要置空,否则访问到的这个指针就会变成野指针;
* 若是访问不到没关系
*
* --》头指针和尾指针需要置空
*/
#include "queue.h"
void test()
{
Queue q;
QueueInit(&q);
QueuePush(&q, 1);
QueuePush(&q, 2);
QueuePush(&q, 3);
QueuePush(&q, 4);
if (QueueEmpty(&q))
printf("队列为空\n");
else
printf("队列不为空\n");
printf("队列大小为:%d\n", QueueSize(&q));
while (!QueueEmpty(&q))
{
printf("队头元素为:%d\n",QueueFront(&q));
QueuePop(&q);
}
if (QueueEmpty(&q))
printf("队列为空\n");
else
printf("队列不为空\n");
printf("队列大小为:%d\n", QueueSize(&q));
QueueDestroy(&q);
}
int main(void)
{
test();
return 0;
}
OJ题目实训
⌨【LeetCode】225.用队列实现栈
链接
⌨【LeetCode】232.用栈实现队列
链接
⌨【LeetCode】622.设计环形队列
链接
栈与队列的实际应用
对于【栈与队列】,可以看出,并没有我们之前实现的顺序表和链表那么复杂,也正是因为如此,它在显示生活中就广泛地被使用到,我们一起来聊聊和这个
后缀表达式——栈
- 这个我之前有写过一篇文章,可以去看看—》数据结构之后缀表达式
浏览器的前进后退——栈
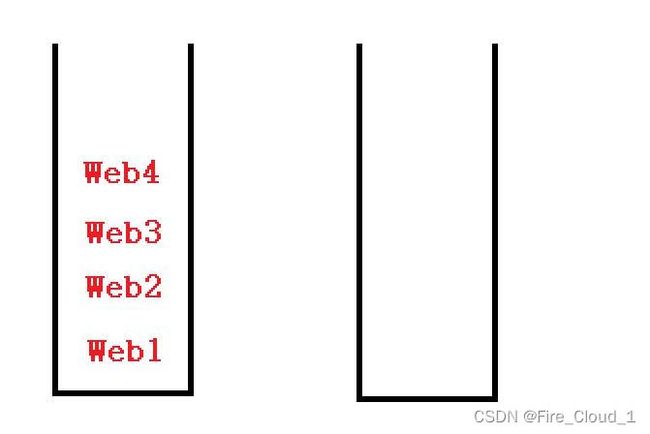
- 对于这个,我是在一本书《数据结构与算法之美》上看到的,我觉得非常巧妙,对于我们日常使用的浏览器,也就是左上角的这个前进后退功能,竟然也可以使用栈来模拟。
- 具体的话就是使用两个栈,也就是将打开过的每一个网页放入第一个栈
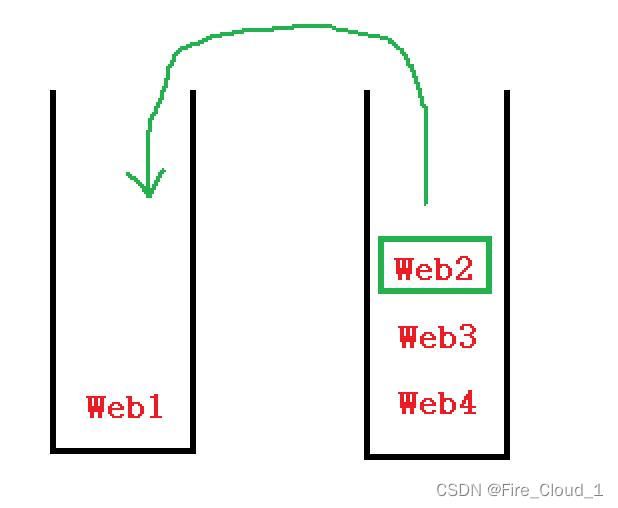
- 当想要浏览当前网站的前一个网站,就将栈顶的这个网站出栈,然后放入第二个栈中,接着取出第一个栈的栈顶元素即可
- 然后若是你想要去实现一个前进功能,也就是回到上次退回去的页面,只需要将第二个栈中的栈顶元素出栈,重新放回到第一个栈中,便可以继续访问了
- 之后有机会也写一篇有关这个的磨博客
业务办理系统——队列
- 对于队列来说,显示中用的最多除了排队系统就是这种业务办理系统了,其实这也是一种排队系统,类似于一种抽号机,需要办理业务的客户先去抽号机取号,一一排队等待业务窗口开始办理,抽到前面序号的先办理,刚好实现了队列FIFO的原理
- 但是这里可能会碰到两个窗口同时叫到同一个号的情况,这个的话会涉及到我们后面所要学的线程同步方面的知识,假如说一个窗口开始叫号了,那么就用一个锁将另一个窗口锁起来,就不会发生冲突了,具体的我们之后学到再说
迷宫问题——栈与队列
- 这个我之前也有写过一篇文章,可以去看看—》栈与队列实现迷宫问题
总结与提炼
- 好,来总结一下本文所学到的知识,在上文中,我为大家介绍了两种数据结构,分别是【栈】和【队列】,对于它们的实现我是使用的【顺序栈】和【链式队】,当然你还可以去实现他们的另一种结构,我这里只是讲的最优结果。讲解完了它们的接口算法实现,接下去我们通过三道算法题加深了对栈与队列的理解,于是可以想到将她们应用到实际生活中去,讲了四个有关栈与队列的实际应用,你觉得形象吗