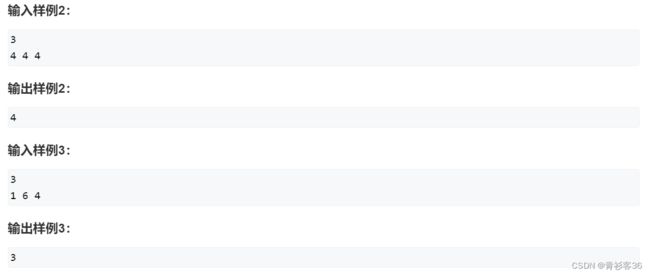
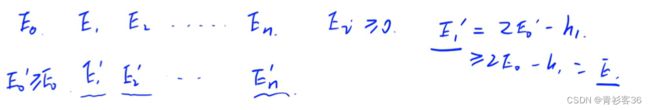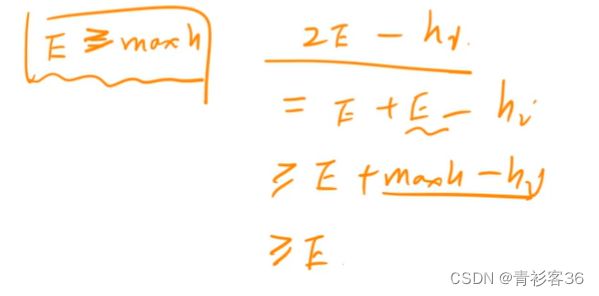- 斤斤计较的婚姻到底有多难?
白心之岂必有为
很多人私聊我会问到在哪个人群当中斤斤计较的人最多?我都会回答他,一般婚姻出现问题的斤斤计较的人士会非常多,以我多年经验,在婚姻落的一塌糊涂的人当中,斤斤计较的人数占比在20~30%以上,也就是说10个婚姻出现问题的斤斤计较的人有2-3个有多不减。在婚姻出问题当中,有大量的心理不平衡的、尖酸刻薄的怨妇。在婚姻中仅斤斤计较有两种类型:第一种是物质上的,另一种是精神上的。在物质与精神上抠门已经严重的影响
- QQ群采集助手,精准引流必备神器
2401_87347160
其他经验分享
功能概述微信群查找与筛选工具是一款专为微信用户设计的辅助工具,它通过关键词搜索功能,帮助用户快速找到相关的微信群,并提供筛选是否需要验证的群组的功能。主要功能关键词搜索:用户可以输入关键词,工具将自动查找包含该关键词的微信群。筛选功能:工具提供筛选机制,用户可以选择是否只显示需要验证或不需要验证的群组。精准引流:通过上述功能,用户可以更精准地找到目标群组,进行有效的引流操作。3.设备需求该工具可以
- 机器学习与深度学习间关系与区别
ℒℴѵℯ心·动ꦿ໊ོ꫞
人工智能学习深度学习python
一、机器学习概述定义机器学习(MachineLearning,ML)是一种通过数据驱动的方法,利用统计学和计算算法来训练模型,使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本,识别其中的模式和规律,从而对新的数据进行判断。其核心在于通过训练过程,让模型不断优化和提升其预测准确性。主要类型1.监督学习(SupervisedLearning)监督学习是指在训练数据集中包含输入
- 随笔 | 仙一般的灵气
海思沧海
仙岛今天,我看了你全部,似乎已经进入你的世界我不知道,这是否是梦幻,还是你仙一般的灵气吸引了我也许每一个人都要有一份属于自己的追求,这样才能够符合人生的梦想,生活才能够充满着阳光与快乐我不知道,我为什么会这样的感叹,是在感叹自己的人生,还是感叹自己一直没有孜孜不倦的追求只感觉虚度了光阴,每天活在自己的梦中,活在一个不真实的世界是在逃避自己,还是在逃避周围的一切有时候我嘲笑自己,嘲笑自己如此的虚无,
- 一百九十四章. 自相矛盾
巨木擎天
唉!就这么一夜,林子感觉就像过了很多天似的,先是回了阳间家里,遇到了那么多不可思议的事情儿。特别是小伙伴们,第二次与自己见面时,僵硬的表情和恐怖的气氛,让自己如坐针毡,打从心眼里难受!还有东子,他现在还好吗?有没有被人欺负?护城河里的小鱼小虾们,还都在吗?水不会真的干枯了吧?那对相亲相爱漂亮的太平鸟儿,还好吧!春天了,到了做窝、下蛋、喂养小鸟宝宝的时候了,希望它们都能够平安啊!虽然没有看见家人,也
- 微服务下功能权限与数据权限的设计与实现
nbsaas-boot
微服务java架构
在微服务架构下,系统的功能权限和数据权限控制显得尤为重要。随着系统规模的扩大和微服务数量的增加,如何保证不同用户和服务之间的访问权限准确、细粒度地控制,成为设计安全策略的关键。本文将讨论如何在微服务体系中设计和实现功能权限与数据权限控制。1.功能权限与数据权限的定义功能权限:指用户或系统角色对特定功能的访问权限。通常是某个用户角色能否执行某个操作,比如查看订单、创建订单、修改用户资料等。数据权限:
- 学点心理知识,呵护孩子健康
静候花开_7090
昨天听了华中师范大学教育管理学系副教授张玲老师的《哪里才是学生心理健康的最后庇护所,超越教育与技术的思考》的讲座。今天又重新学习了一遍,收获匪浅。张玲博士也注意到了当今社会上的孩子由于心理问题导致的自残、自杀及伤害他人等恶性事件。她向我们普及了一个重要的命题,她说心理健康的一些基本命题,我们与我们通常的一些教育命题是不同的,她还举了几个例子,让我们明白我们原来以为的健康并非心理学上的健康。比如如果
- c++ 的iostream 和 c++的stdio的区别和联系
黄卷青灯77
c++算法开发语言iostreamstdio
在C++中,iostream和C语言的stdio.h都是用于处理输入输出的库,但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系:区别1.编程风格iostream(C++风格):C++标准库中的输入输出流类库,支持面向对象的输入输出操作。典型用法是cin(输入)和cout(输出),使用>操作符来处理数据。更加类型安全,支持用户自定义类型的输入输出。#includeintmain(){in
- 《投行人生》读书笔记
小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅,比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力,更多的是自我意识,你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议,细节,截止日期和数据很重要截止日期,一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
- Long类型前后端数据不一致
igotyback
前端
响应给前端的数据浏览器控制台中response中看到的Long类型的数据是正常的到前端数据不一致前后端数据类型不匹配是一个常见问题,尤其是当后端使用Java的Long类型(64位)与前端JavaScript的Number类型(最大安全整数为2^53-1,即16位)进行数据交互时,很容易出现精度丢失的问题。这是因为JavaScript中的Number类型无法安全地表示超过16位的整数。为了解决这个问
- 店群合一模式下的社区团购新发展——结合链动 2+1 模式、AI 智能名片与 S2B2C 商城小程序源码
说私域
人工智能小程序
摘要:本文探讨了店群合一的社区团购平台在当今商业环境中的重要性和优势。通过分析店群合一模式如何将互联网社群与线下终端紧密结合,阐述了链动2+1模式、AI智能名片和S2B2C商城小程序源码在这一模式中的应用价值。这些创新元素的结合为社区团购带来了新的机遇,提升了用户信任感、拓展了营销渠道,并实现了线上线下的完美融合。一、引言随着互联网技术的不断发展,社区团购作为一种新兴的商业模式,在满足消费者日常需
- 2021-08-26
影幽
在生活中,女人与男人的感悟往往有所不同。人生最大的舞台就是生活,大幕随时都可能拉开,关键是你愿不愿意表演都无法躲避。在生活中,遇事不要急躁,不要急于下结论,尤其生气时不要做决断,要学会换位思考,大事化小小事化了,把复杂的事情尽量简单处理,千万不要把简单的事情复杂化。永远不要扭曲,别人善意,无药可救。昨天是张过期的支票,明天是张信用卡,只有今天才是现金,要善加利用!执着的攀登者不必去与别人比较自己的
- 高级编程--XML+socket练习题
masa010
java开发语言
1.北京华北2114.8万人上海华东2,500万人广州华南1292.68万人成都华西1417万人(1)使用dom4j将信息存入xml中(2)读取信息,并打印控制台(3)添加一个city节点与子节点(4)使用socketTCP协议编写服务端与客户端,客户端输入城市ID,服务器响应相应城市信息(5)使用socketTCP协议编写服务端与客户端,客户端要求用户输入city对象,服务端接收并使用dom4j
- 2018-07-23-催眠日作业-#不一样的31天#-66小鹿
小鹿_33
预言日:人总是在逃避命运的路上,与之不期而遇。心理学上有个著名的名词,叫做自证预言;经济学上也有一个很著名的定律叫做,墨菲定律;在灵修派上,还有一个很著名的法则,叫做吸引力法则。这3个领域的词,虽然看起来不太一样,但是他们都在告诉人们一个现象:你越担心什么,就越有可能会发生什么。同样的道理,你越想得到什么,就应该要积极地去创造什么。无论是自证预言,墨菲定律还是吸引力法则,对人都有正反2个维度的影响
- 回溯 Leetcode 332 重新安排行程
mmaerd
Leetcode刷题学习记录leetcode算法职场和发展
重新安排行程Leetcode332学习记录自代码随想录给你一份航线列表tickets,其中tickets[i]=[fromi,toi]表示飞机出发和降落的机场地点。请你对该行程进行重新规划排序。所有这些机票都属于一个从JFK(肯尼迪国际机场)出发的先生,所以该行程必须从JFK开始。如果存在多种有效的行程,请你按字典排序返回最小的行程组合。例如,行程[“JFK”,“LGA”]与[“JFK”,“LGB
- 每日一题——第九十题
互联网打工人no1
C语言程序设计每日一练c语言
题目:判断子串是否与主串匹配#include#include#include//////判断子串是否在主串中匹配//////主串///子串///boolisSubstring(constchar*str,constchar*substr){intlenstr=strlen(str);//计算主串的长度intlenSub=strlen(substr);//计算子串的长度//遍历主字符串,对每个可能得
- Python数据分析与可视化实战指南
William数据分析
pythonpython数据
在数据驱动的时代,Python因其简洁的语法、强大的库生态系统以及活跃的社区,成为了数据分析与可视化的首选语言。本文将通过一个详细的案例,带领大家学习如何使用Python进行数据分析,并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前,我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
- 《庄子.达生9》
钱江潮369
【原文】孔子观于吕梁,县水三十仞,流沫四十里,鼋鼍鱼鳖之所不能游也。见一丈夫游之,以为有苦而欲死也,使弟子并流而拯之。数百步而出,被发行歌而游于塘下。孔子从而问焉,曰:“吾以子为鬼,察子则人也。请问,‘蹈水有道乎’”曰:“亡,吾无道。吾始乎故,长乎性,成乎命。与齐俱入,与汩偕出,从水之道而不为私焉。此吾所以蹈之也。”孔子曰:“何谓始乎故,长乎性,成乎命?”曰:“吾生于陵而安于陵,故也;长于水而安于
- 水泥质量纠纷案代理词
徐宝峰律师
贵州领航建设有限公司诉贵州纳雍隆庆乌江水泥有限公司产品质量纠纷案代理词尊敬的审判长、审判员:贵州千里律师事务所接受被告贵州纳雍隆庆乌江水泥有限公司的委托,指派我担任其诉讼代理人,参加本案的诉讼活动。下面,我结合本案事实和相关法律规定发表如下代理意见,供合议庭评议案件时参考:原告应当举证证明其遭受的损失与被告生产的水泥质量的因果关系。首先水泥是一种粉状水硬性无机胶凝材料。加水搅拌后成浆体,能在空气中
- Goolge earth studio 进阶4——路径修改与平滑
陟彼高冈yu
Googleearthstudio进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径,所以当我们通过这个关键帧时,不是一个生硬的角度,而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄,允许我们调整路径的形状。右键单击,我们可以选择“平滑路径”,这是默认的自动平滑算法,或者我们可
- 基于社交网络算法优化的二维最大熵图像分割
智能算法研学社(Jack旭)
智能优化算法应用图像分割算法php开发语言
智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用:基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果:5.参考文献:6.Matlab代码摘要:本文介绍基于最大熵的图像分割,并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前,请阅读《图像分割:直方图区域划分及信息统计介绍》htt
- 18-115 一切思考不能有效转化为行动,都TM是扯淡!
成长时间线
7月25号写了一篇关于为什么会断更如此严重的反思,然而,之后日更仅仅维持了一周,又出现了这次更严重的现象。从8月2号到昨天8月6号,5天!又是5天没有更文!虽然这次断更时间和上次一样,那为什么说这次更严重?因为上次之后就分析了问题的原因,以及应该如何解决,按理说应该会好转,然而,没过几天严重断更的现象再次出现,想想,经过反思,问题依然没有解决与改变,这让我有些担忧。到底是哪里出了问题,难道我就真的
- 山东大学小树林支教调研团青青仓木队——翟晓楠
山东大学青青仓木队
过了半年,又一次启程,又一次回到支教的初心之地。比起上一次的试探与不安,我更多了一丝稳重与熟练。心境、处境也都随着半个学期的过去而变得不同,半个学期中,身体上的,心理上的,太多的逆境让我变得步履维艰,曲曲折折,弯弯绕绕,我仿佛打不起精神,没有胃口,没有动力。感觉走的不顺畅的时候,支教这个旅程,给了我力量。自告奋勇承担起队长这一职务的我,从组织时的复杂和困难的经历,协调各种问题,从无到有,和校长和队
- 直返最高等级与直返APP:无需邀请码的返利新体验
古楼
随着互联网的普及和电商的兴起,直返模式逐渐成为一种流行的商业模式。在这种模式下,消费者通过购买产品或服务,获得一定的返利,并可以分享给更多的人。其中,直返最高等级和直返APP是直返模式中的重要概念和工具。本文将详细介绍直返最高等级的概念、直返APP的使用以及与邀请码的关系。【高省】APP(高佣金领导者)是一个自用省钱佣金高,分享推广赚钱多的平台,百度有几百万篇报道,运行三年,稳定可靠。高省APP,
- DIV+CSS+JavaScript技术制作网页(旅游主题网页设计与制作)云南大理
STU学生网页设计
网页设计期末网页作业html静态网页html5期末大作业网页设计web大作业
️精彩专栏推荐作者主页:【进入主页—获取更多源码】web前端期末大作业:【HTML5网页期末作业(1000套)】程序员有趣的告白方式:【HTML七夕情人节表白网页制作(110套)】文章目录二、网站介绍三、网站效果▶️1.视频演示2.图片演示四、网站代码HTML结构代码CSS样式代码五、更多源码二、网站介绍网站布局方面:计划采用目前主流的、能兼容各大主流浏览器、显示效果稳定的浮动网页布局结构。网站程
- 2020-04-12每天三百字之连接与替代
冷眼看潮
不知道是不是好为人师,有时候还真想和别人分享一下我对某些现象的看法或者解释。人类社会不断发展进步的过程,就是不断连接与替代的过程。人类发现了火并应用火以后,告别了茹毛饮血的野兽般的原始生活(火烧、烹饪替代了生食)人类用石器代替了完全手工,工具的使用使人类进步一大步。类似这样的替代还有很多,随着科技的发展,有更多的原始的事物被替代,代之以更高效、更先进的技术。在近现代,汽车替代了马车,高速公路和铁路
- 探索OpenAI和LangChain的适配器集成:轻松切换模型提供商
nseejrukjhad
langchaineasyui前端python
#探索OpenAI和LangChain的适配器集成:轻松切换模型提供商##引言在人工智能和自然语言处理的世界中,OpenAI的模型提供了强大的能力。然而,随着技术的发展,许多人开始探索其他模型以满足特定需求。LangChain作为一个强大的工具,集成了多种模型提供商,通过提供适配器,简化了不同模型之间的转换。本篇文章将介绍如何使用LangChain的适配器与OpenAI集成,以便轻松切换模型提供商
- 利用Requests Toolkit轻松完成HTTP请求
nseejrukjhad
http网络协议网络python
RequestsToolkit的力量:轻松构建HTTP请求Agent在现代软件开发中,API请求是与外部服务交互的核心。RequestsToolkit提供了一种便捷的方式,帮助开发者构建自动化的HTTP请求Agent。本文旨在详细介绍RequestsToolkit的设置、使用和潜在挑战。引言RequestsToolkit是一个强大的工具包,可用于构建执行HTTP请求的智能代理。这对于想要自动化与外
- 数组去重
好奇的猫猫猫
整理自js中基础数据结构数组去重问题思考?如何去除数组中重复的项例如数组:[1,3,4,3,5]我们在做去重的时候,一开始想到的肯定是,逐个比较,外面一层循环,内层后一个与前一个一比较,如果是久不将当前这一项放进新的数组,挨个比较完之后返回一个新的去过重复的数组不好的实践方式上述方法效率极低,代码量还多,思考?有没有更好的方法这时候不禁一想当然有了!!!hashtable啊,通过对象的hash办法
- 春季养肝正当时
dxn悟
重温快乐2023年2月4日立春。春天来了,春暖花开,小鸟欢唱,那在这样的季节我们如何养肝呢?自然界的春季对应中医五行的木,人体五脏肝属木,“木曰曲直”,是以树干曲曲直直地向上、向外伸长舒展的生发姿态,来形容具有生长、升发、条达、舒畅等特征的食物及现象。根据中医天人相应的理念,肝五行属木,喜条达,主疏泄,与春天相应,所以春天最适合养肝。养肝首先要少生气,因为肝喜条达恶抑郁。人体五志肝为怒,生气发怒最
- 开发者关心的那些事
圣子足道
ios游戏编程apple支付
我要在app里添加IAP,必须要注册自己的产品标识符(product identifiers)。产品标识符是什么?
产品标识符(Product Identifiers)是一串字符串,它用来识别你在应用内贩卖的每件商品。App Store用产品标识符来检索产品信息,标识符只能包含大小写字母(A-Z)、数字(0-9)、下划线(-)、以及圆点(.)。你可以任意排列这些元素,但我们建议你创建标识符时使用
- 负载均衡器技术Nginx和F5的优缺点对比
bijian1013
nginxF5
对于数据流量过大的网络中,往往单一设备无法承担,需要多台设备进行数据分流,而负载均衡器就是用来将数据分流到多台设备的一个转发器。
目前有许多不同的负载均衡技术用以满足不同的应用需求,如软/硬件负载均衡、本地/全局负载均衡、更高
- LeetCode[Math] - #9 Palindrome Number
Cwind
javaAlgorithm题解LeetCodeMath
原题链接:#9 Palindrome Number
要求:
判断一个整数是否是回文数,不要使用额外的存储空间
难度:简单
分析:
题目限制不允许使用额外的存储空间应指不允许使用O(n)的内存空间,O(1)的内存用于存储中间结果是可以接受的。于是考虑将该整型数反转,然后与原数字进行比较。
注:没有看到有关负数是否可以是回文数的明确结论,例如
- 画图板的基本实现
15700786134
画图板
要实现画图板的基本功能,除了在qq登陆界面中用到的组件和方法外,还需要添加鼠标监听器,和接口实现。
首先,需要显示一个JFrame界面:
public class DrameFrame extends JFrame { //显示
- linux的ps命令
被触发
linux
Linux中的ps命令是Process Status的缩写。ps命令用来列出系统中当前运行的那些进程。ps命令列出的是当前那些进程的快照,就是执行ps命令的那个时刻的那些进程,如果想要动态的显示进程信息,就可以使用top命令。
要对进程进行监测和控制,首先必须要了解当前进程的情况,也就是需要查看当前进程,而 ps 命令就是最基本同时也是非常强大的进程查看命令。使用该命令可以确定有哪些进程正在运行
- Android 音乐播放器 下一曲 连续跳几首歌
肆无忌惮_
android
最近在写安卓音乐播放器的时候遇到个问题。在MediaPlayer播放结束时会回调
player.setOnCompletionListener(new OnCompletionListener() {
@Override
public void onCompletion(MediaPlayer mp) {
mp.reset();
Log.i("H
- java导出txt文件的例子
知了ing
javaservlet
代码很简单就一个servlet,如下:
package com.eastcom.servlet;
import java.io.BufferedOutputStream;
import java.io.IOException;
import java.net.URLEncoder;
import java.sql.Connection;
import java.sql.Resu
- Scala stack试玩, 提高第三方依赖下载速度
矮蛋蛋
scalasbt
原文地址:
http://segmentfault.com/a/1190000002894524
sbt下载速度实在是惨不忍睹, 需要做些配置优化
下载typesafe离线包, 保存为ivy本地库
wget http://downloads.typesafe.com/typesafe-activator/1.3.4/typesafe-activator-1.3.4.zip
解压r
- phantomjs安装(linux,附带环境变量设置) ,以及casperjs安装。
alleni123
linuxspider
1. 首先从官网
http://phantomjs.org/下载phantomjs压缩包,解压缩到/root/phantomjs文件夹。
2. 安装依赖
sudo yum install fontconfig freetype libfreetype.so.6 libfontconfig.so.1 libstdc++.so.6
3. 配置环境变量
vi /etc/profil
- JAVA IO FileInputStream和FileOutputStream,字节流的打包输出
百合不是茶
java核心思想JAVA IO操作字节流
在程序设计语言中,数据的保存是基本,如果某程序语言不能保存数据那么该语言是不可能存在的,JAVA是当今最流行的面向对象设计语言之一,在保存数据中也有自己独特的一面,字节流和字符流
1,字节流是由字节构成的,字符流是由字符构成的 字节流和字符流都是继承的InputStream和OutPutStream ,java中两种最基本的就是字节流和字符流
类 FileInputStream
- Spring基础实例(依赖注入和控制反转)
bijian1013
spring
前提条件:在http://www.springsource.org/download网站上下载Spring框架,并将spring.jar、log4j-1.2.15.jar、commons-logging.jar加载至工程1.武器接口
package com.bijian.spring.base3;
public interface Weapon {
void kil
- HR看重的十大技能
bijian1013
提升能力HR成长
一个人掌握何种技能取决于他的兴趣、能力和聪明程度,也取决于他所能支配的资源以及制定的事业目标,拥有过硬技能的人有更多的工作机会。但是,由于经济发展前景不确定,掌握对你的事业有所帮助的技能显得尤为重要。以下是最受雇主欢迎的十种技能。 一、解决问题的能力 每天,我们都要在生活和工作中解决一些综合性的问题。那些能够发现问题、解决问题并迅速作出有效决
- 【Thrift一】Thrift编译安装
bit1129
thrift
什么是Thrift
The Apache Thrift software framework, for scalable cross-language services development, combines a software stack with a code generation engine to build services that work efficiently and s
- 【Avro三】Hadoop MapReduce读写Avro文件
bit1129
mapreduce
Avro是Doug Cutting(此人绝对是神一般的存在)牵头开发的。 开发之初就是围绕着完善Hadoop生态系统的数据处理而开展的(使用Avro作为Hadoop MapReduce需要处理数据序列化和反序列化的场景),因此Hadoop MapReduce集成Avro也就是自然而然的事情。
这个例子是一个简单的Hadoop MapReduce读取Avro格式的源文件进行计数统计,然后将计算结果
- nginx定制500,502,503,504页面
ronin47
nginx 错误显示
server {
listen 80;
error_page 500/500.html;
error_page 502/502.html;
error_page 503/503.html;
error_page 504/504.html;
location /test {return502;}}
配置很简单,和配
- java-1.二叉查找树转为双向链表
bylijinnan
二叉查找树
import java.util.ArrayList;
import java.util.List;
public class BSTreeToLinkedList {
/*
把二元查找树转变成排序的双向链表
题目:
输入一棵二元查找树,将该二元查找树转换成一个排序的双向链表。
要求不能创建任何新的结点,只调整指针的指向。
10
/ \
6 14
/ \
- Netty源码学习-HTTP-tunnel
bylijinnan
javanetty
Netty关于HTTP tunnel的说明:
http://docs.jboss.org/netty/3.2/api/org/jboss/netty/channel/socket/http/package-summary.html#package_description
这个说明有点太简略了
一个完整的例子在这里:
https://github.com/bylijinnan
- JSONUtil.serialize(map)和JSON.toJSONString(map)的区别
coder_xpf
jqueryjsonmapval()
JSONUtil.serialize(map)和JSON.toJSONString(map)的区别
数据库查询出来的map有一个字段为空
通过System.out.println()输出 JSONUtil.serialize(map): {"one":"1","two":"nul
- Hibernate缓存总结
cuishikuan
开源sshjavawebhibernate缓存三大框架
一、为什么要用Hibernate缓存?
Hibernate是一个持久层框架,经常访问物理数据库。
为了降低应用程序对物理数据源访问的频次,从而提高应用程序的运行性能。
缓存内的数据是对物理数据源中的数据的复制,应用程序在运行时从缓存读写数据,在特定的时刻或事件会同步缓存和物理数据源的数据。
二、Hibernate缓存原理是怎样的?
Hibernate缓存包括两大类:Hib
- CentOs6
dalan_123
centos
首先su - 切换到root下面1、首先要先安装GCC GCC-C++ Openssl等以来模块:yum -y install make gcc gcc-c++ kernel-devel m4 ncurses-devel openssl-devel2、再安装ncurses模块yum -y install ncurses-develyum install ncurses-devel3、下载Erang
- 10款用 jquery 实现滚动条至页面底端自动加载数据效果
dcj3sjt126com
JavaScript
无限滚动自动翻页可以说是web2.0时代的一项堪称伟大的技术,它让我们在浏览页面的时候只需要把滚动条拉到网页底部就能自动显示下一页的结果,改变了一直以来只能通过点击下一页来翻页这种常规做法。
无限滚动自动翻页技术的鼻祖是微博的先驱:推特(twitter),后来必应图片搜索、谷歌图片搜索、google reader、箱包批发网等纷纷抄袭了这一项技术,于是靠滚动浏览器滚动条
- ImageButton去边框&Button或者ImageButton的背景透明
dcj3sjt126com
imagebutton
在ImageButton中载入图片后,很多人会觉得有图片周围的白边会影响到美观,其实解决这个问题有两种方法
一种方法是将ImageButton的背景改为所需要的图片。如:android:background="@drawable/XXX"
第二种方法就是将ImageButton背景改为透明,这个方法更常用
在XML里;
<ImageBut
- JSP之c:foreach
eksliang
jspforearch
原文出自:http://www.cnblogs.com/draem0507/archive/2012/09/24/2699745.html
<c:forEach>标签用于通用数据循环,它有以下属性 属 性 描 述 是否必须 缺省值 items 进行循环的项目 否 无 begin 开始条件 否 0 end 结束条件 否 集合中的最后一个项目 step 步长 否 1
- Android实现主动连接蓝牙耳机
gqdy365
android
在Android程序中可以实现自动扫描蓝牙、配对蓝牙、建立数据通道。蓝牙分不同类型,这篇文字只讨论如何与蓝牙耳机连接。
大致可以分三步:
一、扫描蓝牙设备:
1、注册并监听广播:
BluetoothAdapter.ACTION_DISCOVERY_STARTED
BluetoothDevice.ACTION_FOUND
BluetoothAdapter.ACTION_DIS
- android学习轨迹之四:org.json.JSONException: No value for
hyz301
json
org.json.JSONException: No value for items
在JSON解析中会遇到一种错误,很常见的错误
06-21 12:19:08.714 2098-2127/com.jikexueyuan.secret I/System.out﹕ Result:{"status":1,"page":1,&
- 干货分享:从零开始学编程 系列汇总
justjavac
编程
程序员总爱重新发明轮子,于是做了要给轮子汇总。
从零开始写个编译器吧系列 (知乎专栏)
从零开始写一个简单的操作系统 (伯乐在线)
从零开始写JavaScript框架 (图灵社区)
从零开始写jQuery框架 (蓝色理想 )
从零开始nodejs系列文章 (粉丝日志)
从零开始编写网络游戏
- jquery-autocomplete 使用手册
macroli
jqueryAjax脚本
jquery-autocomplete学习
一、用前必备
官方网站:http://bassistance.de/jquery-plugins/jquery-plugin-autocomplete/
当前版本:1.1
需要JQuery版本:1.2.6
二、使用
<script src="./jquery-1.3.2.js" type="text/ja
- PLSQL-Developer或者Navicat等工具连接远程oracle数据库的详细配置以及数据库编码的修改
超声波
oracleplsql
在服务器上将Oracle安装好之后接下来要做的就是通过本地机器来远程连接服务器端的oracle数据库,常用的客户端连接工具就是PLSQL-Developer或者Navicat这些工具了。刚开始也是各种报错,什么TNS:no listener;TNS:lost connection;TNS:target hosts...花了一天的时间终于让PLSQL-Developer和Navicat等这些客户
- 数据仓库数据模型之:极限存储--历史拉链表
superlxw1234
极限存储数据仓库数据模型拉链历史表
在数据仓库的数据模型设计过程中,经常会遇到这样的需求:
1. 数据量比较大; 2. 表中的部分字段会被update,如用户的地址,产品的描述信息,订单的状态等等; 3. 需要查看某一个时间点或者时间段的历史快照信息,比如,查看某一个订单在历史某一个时间点的状态, 比如,查看某一个用户在过去某一段时间内,更新过几次等等; 4. 变化的比例和频率不是很大,比如,总共有10
- 10点睛Spring MVC4.1-全局异常处理
wiselyman
spring mvc
10.1 全局异常处理
使用@ControllerAdvice注解来实现全局异常处理;
使用@ControllerAdvice的属性缩小处理范围
10.2 演示
演示控制器
package com.wisely.web;
import org.springframework.stereotype.Controller;
import org.spring