数据结构——栈的基本实现与讲解(C++描述)
栈的定义
栈(stack)又名堆栈,它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。 ——百度百科
简单定义:栈就是一种只允许在表尾进行插入和删除操作的线性表
如何理解栈的概念
① 举一个生活中的例子:我在一个储物箱中,堆了一堆衣服,我的一件球衣在最下面,而我要拿这件衣服,就意味着我必须将上面的衣服全部拿出来才可以,但是由于箱子只有一个口,我也只能从上面拿东西,心里还默默想着,当初就不该将球衣早早的放进去,导致结果就是先进后出!
你就不能举个计算机中的例子?这就安排!
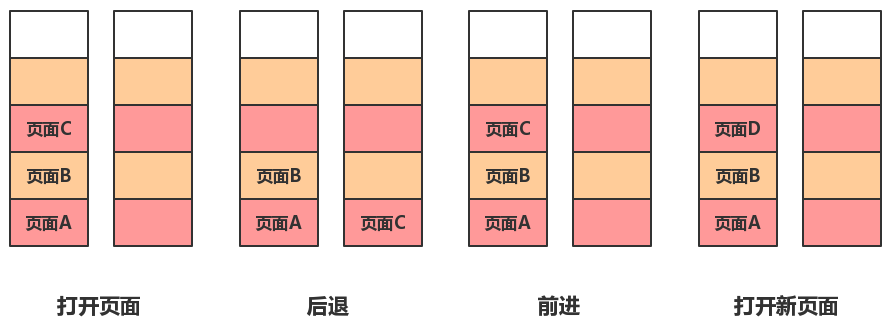
② 计算机中很多操作都是使用栈的原理来实现的,我们就比如常见的浏览器中的 “前进键” “后退键” 就可以利用栈的原理来实现,我们来用图说明一下
我们想要实现前进后退,可以使用两个栈(暂时称作 M、N)来实现
我们分别浏览了页面A、页面B、页面C,所以我们将这些页面依次压入栈,即图中打开页面部分
当用户点击后退时,我们需要退回到页面B中去,但是由于页面C在B上方,我们就必须将页面C从栈M中先弹出,放到栈N中,即图中后退部分
但是如果用户突然又想回到页面C去,原理相似的,只需要把栈N中的页面C弹出,重新压入栈M即可
而如果用户在浏览B界面的时候,打开了新的界面D,那么C就无法通过前进后退访问了,所以栈M中压入页面D的同时还需要清空栈N
栈的术语说明
栈顶:允许进行插入和进行删除操作的一段成为栈顶
栈底:表的另一端称为栈底 (第一个元素进入的位置)
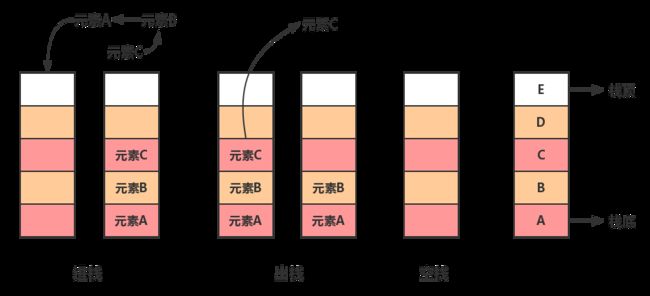
压栈:在栈顶位置插入元素的操作叫做压栈,或入栈、进栈
出栈:删除栈顶元素的操作叫做出栈,也叫作弹栈,或者退栈
空栈:不含元素的空表
栈溢出:当栈满的时候,如果再有元素压栈,则发生上溢,当栈空的时候,再出栈则发生下溢
栈的抽象数据类型
#ifndef _STACK_H_
#define _STACK_H_
#include
using namespace std;
template
class Stack {
public:
virtual bool empty() const = 0;
virtual int size() const = 0;
virtual void push(const T &x) = 0;
virtual T pop() = 0;
virtual T getTop() const = 0;
virtual void clear() =0;
virtual ~Stack() {}
};
/*
自定义异常类
*/
// 用于检查范围的有效性
class outOfRange:public exception {
public:
const char* what()const throw()
{ return "ERROR! OUT OF RANGE.\n"; }
};
// 用于检查长度的有效性
class badSize:public exception {
public:
const char* what()const throw()
{ return "ERROR! BAD SIZE.\n"; }
};
#endif
顺序栈——栈的顺序存储结构
开头我们就已经提过了,栈实际上就是一种线性表的特例,所以栈的实现和线性表一样,均使用数组实现,我们使用一个一维数组来存储元素,那么总得有个头阿,我们就需要确定栈底的位置,通常我们选择 0 的一端作为栈底,这样更加方便理解与操作,特别的是,我们设置了一个整型变量top 用来存放栈顶元素的位置(下标),也称作栈顶指针
(一) 顺序栈的类型描述
初始的时候,给top赋值-1,表示栈为空,元素进栈以后,top + 1,元素出栈后,top - 1
// array-based stack: definition and implementation for some methods
#ifndef _SEQSTACK_H_
#define _SEQSTACK_H_
#include "Stack.h"
template
class seqStack : public Stack {
private:
T * data;
int top;
int maxSize;
void resize();
public:
seqStack(int initSize = 100) {
if(initSize<=0) throw badSize();
data = new T[initSize];
maxSize = initSize ;
top = -1;
}
~seqStack(){ delete [] data;}
bool empty() const{ return top == -1;}
int size() const{ return top + 1; }
void clear() { top = -1; } // 清空栈内容
void push(const T &value);
T pop();
T getTop() const;
};
#endif
(二) 进栈
template
void seqStack::push(const T &value) {
if (top == maxSize - 1) resize();
data[++top] = value;
}
(三) 出栈
template
T seqStack::pop() {
if(empty())throw outOfRange();
return data[top--];
}
(四) 取栈顶元素
template
T seqStack::getTop() const{
if(empty())throw outOfRange();
return data[top];
}
(五) 扩容
template
void seqStack::resize(){
T * tmp = data;
data = new T[2 * maxSize];
for (int i = 0; i < maxSize; ++i)
data[i] = tmp[i];
maxSize *= 2;
delete[] tmp;
}
(六) 两栈共享空间
栈这种数据结构相比较于线性表,没了有插入和删除的时候需要移动元素的情况,但是仍然有一个比较大的不足,那就是我们必须事先分配空间大小,如果一旦空间满了,再有元素近栈就必须使用编程手段对数组进行扩容,还是比较麻烦的
而有时候我们往往需要多个栈,我们之前的处理手段就是尽量的根据实际问题设计大小合适的数组,但是这显然是有一定难度的,而且常常是这样的,一个栈已经满了,而另一个栈可能还空着很多空间,如果能将那些空闲的位置利用起来就好了,而我们下面就要来提到一个这样的技巧的思路
我们其实就是将两个栈的栈底全部放到了,数组的两端,然后两个栈处于相向位置,逐渐向中间靠拢,只要两个top指针不相遇,两个栈就可以一直用
链栈——栈的链式存储结构
链栈就是使用链式存储结构的栈,和我们在单链表中的链式存储的感觉相似,我们会设置一个指向栈顶的指针top,同时当top == NULL时为空栈
(一) 链栈的类型定义
#ifndef _LINKSTACK_H_
#define _LINKSTACK_H_
#include
#include "Stack.h"
template
class linkStack : public Stack
{
private:
struct Node {
T data;
Node* next;
Node(){ next = NULL; }
Node(const T &value, Node *p = NULL){ data = value; next = p;}
};
Node* top;
public:
linkStack(){ top = NULL; }
~linkStack(){ clear(); }
void clear();
bool empty()const{ return top == NULL; }
int size()const;
void push(const T &value);
T pop();
T getTop()const;
};
#endif
(二) 清空栈
template
void linkStack::clear() {
Node *p;
while (top != NULL) {
p = top;
top = top->next;
delete p;
}
}
(三) 求栈中元素个数
template
int linkStack::size()const {
Node *p = top;
int count = 0;
while (p){
count++;
p = p->next;
}
return count;
}
(四) 进栈
template
void linkStack::push(const T &value) {
Node *p = new Node(value, top);
top = p;
}
(五) 出栈
template
T linkStack::pop() {
if (empty())throw outOfRange();
Node *p = top;
T value = p->data;
top = top->next;
delete p;
return value;
}
(六) 获取栈顶元素
template
T linkStack::getTop() const {
if(empty())throw outOfRange();
return top->data;
}
结尾:
如果文章中有什么不足,或者错误的地方,欢迎大家留言分享想法,感谢朋友们的支持!
如果能帮到你的话,那就来关注我吧!如果您更喜欢微信文章的阅读方式,可以关注我的公众号
在这里的我们素不相识,却都在为了自己的梦而努力 ❤
一个坚持推送原创开发技术文章的公众号:理想二旬不止