遗传算法原理及案例解析
一、遗传算法原理
遗传算法—进化算法(Genetic Algorithm GA)源自达尔文进化论的物竞天择适者生存思想。它是通过模拟生物进化的过程,搜索全局最优解的一种算法。
算法可应用于优化问题,当一个问题有N种解决方案时,如何选择出最优的一组解决方案。
二、算法应用
旅行商问题、求目标函数的全局最大值点问题、特征选择
三、遗传算法求解步骤
设定初始固定规模的种群,种群由每个个体组成,计算每个个体的适应度函数,在进化的过程中,分别经过选择(选择适应度最佳的个体,遗弃适应度较差的个体)、交叉、变异步骤,并不断的重复计算适应度函数、选择、交叉、变异步骤,直到得到最佳的个体(最优解)。
种群相当于多种解的集合,个体相当于每一种解。
在进行遗传算法计算之前需要进行编码(将问题的解空间转换为遗传算法能处理的方式),编码具体分为:二进制编码、符号编码、浮点数编码、格雷编码,以下以二进制编码为例讲解
1)种群初始化(Initial Population)
基因组成染色体,多个染色体组成种群。
2)计算适应度函数(Fitness Function)
计算每个个体适合繁衍下一代的程度(概率)
3)选择(Selection)
选择最合适的个体,并让他们的基因去产生下一代
具体分为:赌轮选择法、排序选择法、最优保存策略
赌轮选择法表述为计算每个个体的概率函数值,将每个个体按照概率函数组成面积为1的赌轮,每转一圈,则概率函数最大的个体更容易被选择。
其中个体的概率函数值为个体的适应度函数值和全部个体的适应度函数值求和的比值
4)交叉(Crossover)
对于每一对要配对的父母,从基因中随机选择交叉点,通过在父母的基因中交叉替换产生子代,子代加入种群。类似染色体的交叉重组
具体分为:一点交叉、二点交叉、一致交叉方法
5)变异(Mutation)
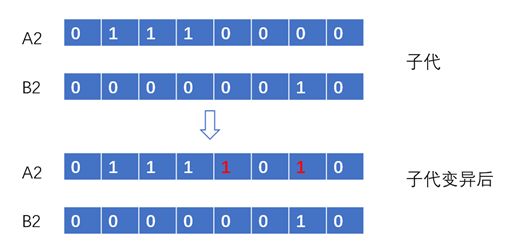
突变的目的是为了维持种群的多样性(保证算法能搜索到解空间中的每一点,找到全局最优解的关键),在子代中允许以低概率随机进行变异,也即是个体的基因会发生突变,例如二进制位翻转
上述的2-5步骤进行迭代计算直到算法收敛。算法收敛条件:当新产生的子代与上一代无明显差异时,则算法终止,最终经过若干次的进化过程,种群中产生适应度最高的个体(该个体代表了问题的解)
其中种群的大小固定,当新一代出生时,较差的一代死去,以维持种群大小不变
四、遗传算法设置参数
种群规模大小(建议值20-200)、变异概率(一般0.005-0.05)、交叉概率(一般0.4-0.99)、进化代数(一般100-500)
五、算法的特点
1)全局最优,对多个解进行评估
2)并行化,同时处理种群中的多个个体
3)搜索方向随机
六、案例及代码实现
6.1旅行商问题的求解
旅行商问题(traveling salesman problem)是一个最优化问题,已知旅行城市数目、前往每个城市的成本,找出一组城市访问的路径使得成本最小,或者说旅行商在拜访的多个地点中,如何找到在拜访每个地点一次后再回到起点的最短路径。
如果要列举所有路径后再决定哪个最佳,那么总路径数量很大,几乎难以计算出来,属于NP问题(所有的非确定性多项式时间可解的判定问题构成NP类问题)。
解决思路
1)加载地图及城市
初始设置城市个数30个,并包含在红色地图边界内
2)计算所有城市之间的距离矩阵
蓝色的圆圈表示旅行商需要经过的城市地点
distances = zeros(cities);
for count1=1:cities,
for count2=1:count1,
x1 = locations(count1,1);
y1 = locations(count1,2);
x2 = locations(count2,1);
y2 = locations(count2,2);
distances(count1,count2)=sqrt((x1-x2)^2+(y1-y2)^2);
distances(count2,count1)=distances(count1,count2);
end;
end;
种群中的个体以有序集表示,种群以元胞数组结构表示
例如种群以P表示,则旅行商要拜访的城市为P{i}。
3)种群初始化
create_permutations.m
function pop = create_permutations(NVARS,FitnessFcn,options)
%种群初始化-创建随机排列的种群.
% The arguments to the function are
% NVARS: 变量大小 Number of variables
% FITNESSFCN: 适应度函数 Fitness function
% OPTIONS: 遗传算法的参数结构 Options structure used by the GA
totalPopulationSize = sum(options.PopulationSize);
n = NVARS;
pop = cell(totalPopulationSize,1);
for i = 1:totalPopulationSize
pop{i} = randperm(n);
end
4)交叉
crossover_permutation.m
function xoverKids = crossover_permutation(parents,options,NVARS, ...
FitnessFcn,thisScore,thisPopulation)
% 旅行商问题的交叉函数—产生子代xoverKids
% The arguments to the function are
% PARENTS: 通过适应度函数选择父代
Parents chosen by the selection function
% OPTIONS: Options created from OPTIMOPTIONS
% NVARS: 变量个数 Number of variables
% FITNESSFCN: 适应度函数 Fitness function
% STATE: State structure used by the GA solver
% THISSCORE:当前种群的评分向量 Vector of scores of the current population
% THISPOPULATION: 当前种群的个体矩阵 Matrix of individuals in the current population
nKids = length(parents)/2;%两个父代产生一个子代
xoverKids = cell(nKids,1); % Normally zeros(nKids,NVARS);
index = 1;
for i=1:nKids
% here is where the special knowledge that the population is a cell
% array is used. Normally, this would be thisPopulation(parents(index),:);
parent = thisPopulation{parents(index)};%通过适应度函数找到父代
index = index + 2;
% Flip a section of parent1.
p1 = ceil((length(parent) -1) * rand);
p2 = p1 + ceil((length(parent) - p1- 1) * rand);
child = parent;
child(p1:p2) = fliplr(child(p1:p2));%从左到右的顺序翻转
xoverKids{i} = child; % Normally, xoverKids(i,:);
end
5)变异
mutate_permutation.m
返回一个变异后的有排列的城市集(种群中的个体)
function mutationChildren = mutate_permutation(parents ,options,NVARS, ...
FitnessFcn, state, thisScore,thisPopulation,mutationRate)
% 旅行商问题的变异函数—产生变异的子代个体
%
% The arguments to the function are
% PARENTS: 通过适应度函数选择的父代Parents chosen by the selection function
% OPTIONS: Options created from OPTIMOPTIONS
% NVARS: 变量个数 Number of variables
% FITNESSFCN: 适应度函数 Fitness function
% STATE: State structure used by the GA solver
% THISSCORE: 当前种群的评分向量Vector of scores of the current population
% THISPOPULATION: 当前种群的个体矩阵Matrix of individuals in the current population
% MUTATIONRATE: 变异率 Rate of mutation
% Here we swap two elements of the permutation
mutationChildren = cell(length(parents),1);% Normally zeros(length(parents),NVARS);
for i=1:length(parents)
parent = thisPopulation{parents(i)}; % Normally thisPopulation(parents(i),:)
p = ceil(length(parent) * rand(1,2)); %一行两列的随机数
child = parent;
child(p(1)) = parent(p(2));
child(p(2)) = parent(p(1));
mutationChildren{i} = child; % Normally mutationChildren(i,:)
end
6)适应度函数
traveling_salesman_fitness.m
function scores = traveling_salesman_fitness(x,distances)
%旅行商问题的适应度函数—返回种群中每个个体的两两城市之间距离的总和
scores = zeros(size(x,1),1);
for j = 1:size(x,1)
% here is where the special knowledge that the population is a cell
% array is used. Normally, this would be pop(j,:);
p = x{j};
f = distances(p(end),p(1));
for i = 2:length(p)
f = f + distances(p(i-1),p(i));
end
scores(j) = f;
end
FitnessFcn= @(x) traveling_salesman_fitness(x,distances);
7)当前最佳路径绘图
traveling_salesman_plot.m
function state = traveling_salesman_plot(options,state,flag,locations)
%旅行商问题的绘图函数—绘制两两城市之间的路线图
persistent x y xx yy
if strcmpi(flag,'init')
load('usborder.mat','x','y','xx','yy');
end
plot(x,y,'Color','red');
axis([-0.1 1.5 -0.2 1.2]);
hold on;
[unused,i] = min(state.Score);
genotype = state.Population{i};
plot(locations(:,1),locations(:,2),'bo');
plot(locations(genotype,1),locations(genotype,2));
hold off
my_plot= @(options,state,flag) traveling_salesman_plot(options, ...
state,flag,locations);
8)遗传算法的参数设置
%种群大小参数 种群类型
options = optimoptions(@ga, 'PopulationType', 'custom','InitialPopulationRange', ...
[1;cities]);
%种群初始化、交叉、变异、绘图、最大代数、种群大小等参数设置
options = optimoptions(options,'CreationFcn',@create_permutations, ...
'CrossoverFcn',@crossover_permutation, ...
'MutationFcn',@mutate_permutation, ...
'PlotFcn', my_plot, ...
'MaxGenerations',500,'PopulationSize',60, ...
'MaxStallGenerations',200,'UseVectorized',true);
遗传算法调用
numberOfVariables = cities;
[x,fval,reason,output] = ...
ga(FitnessFcn,numberOfVariables,[],[],[],[],[],[],[],options)
最终搜索的最佳路径为:
参考文献
[1]Matlab- Custom Data Type Optimization Using the Genetic Algorithm
[2]详解遗传算法-含MATLAB代码
[3]GENETIC ALGORITHMS AS A STRATEGY FOR FEATURE
[4]遗传算法(Genetic Algorithm)
[5]Goldberg_Genetic_Algorithms in Search optimization and mechine learning