1. 前言
这是本人写的第一篇博客(2013年4月5日发在cnblogs上,现在迁移过来),是学习李航老师的《统计学习方法》书以及斯坦福机器学习课Andrew Ng的EM算法课后,对EM算法学习的介绍性笔记,如有写得不恰当或错误的地方,请指出,并多多包涵,谢谢。另外本人数学功底不是很好,有些数学公式我会说明的仔细点的,如果数学基础好,可直接略过。
2.基础数学知识
在正式介绍EM算法之前,先介绍推导EM算法用到的数学基础知识,包括凸函数,Jensen不等式。
2.1.凸函数
对于凸函数,凹函数,如果大家学过高等数学,都应该知道,需要注意的是国内教材如同济大学的《高等数学》的这两个概念跟国外刚好相反,为了能更好的区别,本文章把凹凸函数称之为上凸函数,下凸函数,具体定义如下:
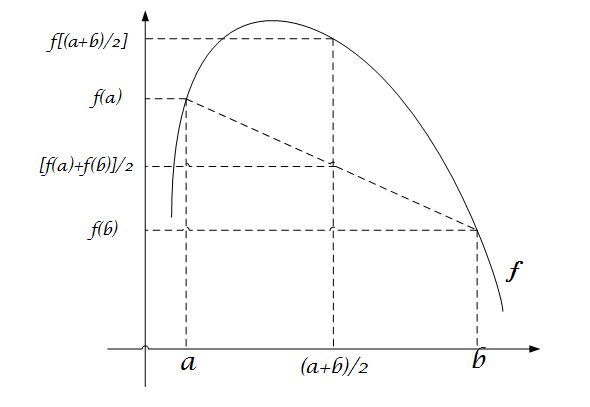
上凸函数:函数 $f(x)$ 满足对定义域上任意两个数 $a$ , $b$ 都有 $f[(a+b)/2] ≥ [f(a)+f(b)]/2$
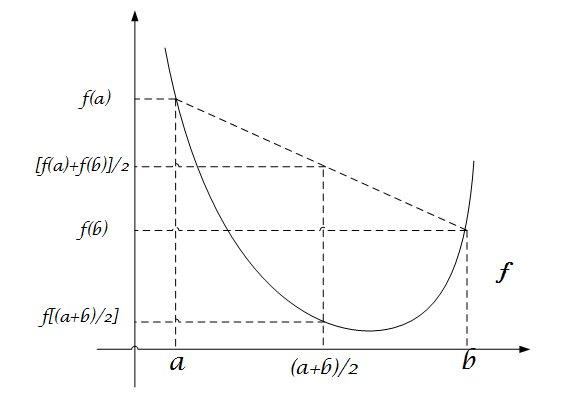
下凸函数:函数 $f(x)$ 满足对定义域上任意两个数 $a$ , $b$ 都有 $f[(a+b)/2] ≤ [f(a)+f(b)]/2$
更直观的可以看图2.1和2.2:
|
|
|---|---|
| 图2.1. 上凸函数 | 图2.2. 下凸函数 |
可以清楚地看到图2.1上凸函数中,$f[(a+b)/2] ≥ [f(a)+f(b)]/2$,而且不难发现,如果f(x)是上凸函数,那么 $-f(x)$ 是下凸函数。
当 $a≠b$ 时,$f[(a+b)/2] > [f(a)+f(b)]/2$ 成立,那么称 $f(x)$ 为严格的上凸函数,等号成立的条件当且仅当 $a=b$,下凸函数与其类似。
2.2.Jensen不等式
有了上述凸函数的定义后,我们就能很清楚的Jensen不等式的含义,它的定义如下:
如果f是上凸函数,$X$ 是随机变量,那么 $f(E[X]) ≥ E[f(X)]$
特别地,如果f是严格上凸函数,那么 $E[f(X)] = f(E[X])$ 当且仅当 $p(X=E[X])=1$,也就是说 $X$ 是常量。
那么很明显 $\log x$ 函数是上凸函数,可以利用这个性质。
有了上述的数学基础知识后,我们就可以看具体的EM算法了。
3.EM算法所解决问题的例子
在推导EM算法之前,先引用《统计学习方法》中EM算法的例子:
例1. (三硬币模型)假设有3枚硬币,分别记作 $A,B,C$ 。这些硬币正面出现的概率分别为 $π$,$p$ 和 $q$。投币实验如下,先投 $A$,如果 $A$ 是正面,即 $A=1$,那么选择投 $B$;$A=0$,投 $C$。最后,如果 $B$ 或者 $C$ 是正面,那么 $y=1$;是反面,那么 $y=0$;独立重复 $n$ 次试验 $(n=10)$,观测结果如下: $1,1,0,1,0,0,1,0,1,1$ 假设只能观测到投掷硬币的结果,不能观测投掷硬币的过程。问如何估计三硬币正面出现的概率,即 $\pi$,$p$ 和 $q$ 的值。
解:设随机变量 $y$ 是观测变量,则投掷一次的概率模型为:$$P(y|\theta)=\pi p^y(1-p)^{1-y}+(1-\pi)q^y(1-q)^{1-y}$$有 $n$ 次观测数据 $Y$,那么观测数据 $Y$ 的似然函数为:$$P(Y|\theta) = \prod_n^{j=1}[\pi p^{y_j}(1-p)^{1-y_j}+(1-\pi)q^{y_j}(1-q)^{1-y_j}]$$那么利用最大似然估计求解模型解,即
\begin{align}
\widehat{\theta}& = \arg \max_{\theta} \log P(Y|\theta)\label{ex:loglikelihood1} \\
& = \arg \max_{\theta} \sum_{j=1}^{10} \log P(y^j|\theta)\label{ex:loglikelihood2} \\
& = \arg \max_{\theta} \sum_{j=1}^{10} \log [\pi p^{y_j}(1-p)^{1-y_j}+(1-\pi)q^{y_j}(1-q)^{1-y_j}]\label{ex:loglikelihood3}
\end{align} 这里将概率模型公式和似然函数代入 $\eqref{ex:loglikelihood1}$ 式中,可以很轻松地推出 $\eqref{ex:loglikelihood1} \Rightarrow \eqref{ex:loglikelihood2} \Rightarrow \eqref{ex:loglikelihood3}$,然后选取 $\theta(\pi,p,q)$,使得 $\eqref{ex:loglikelihood3}$ 式值最大,即最大似然。然后,我们会发现因为 $\eqref{ex:loglikelihood3}$ 中右边多项式 $+$ 符号的存在,使得 $\eqref{ex:loglikelihood3}$ 直接求偏导等于 $\theta$ 或者用梯度下降法都很难求得 $\theta$ 值。
这部分的难点是因为 $\eqref{ex:loglikelihood3}$ 多项式中 $+$ 符号的存在,而这是因为这个三硬币模型中,我们无法得知最后得结果是硬币 $B$ 还是硬币 $C$ 抛出的这个隐藏参数。那么我们把这个latent 随机变量加入到 log-likelihood 函数中,得
\begin{align}
l(\theta)& = \sum_{j=1}^{10}log\: \sum_{i=1}^{2}P(y_{j},z_{i}\mid \theta )\label{ex:latentlog1} \\
& = \sum_{j=1}^{10}log\: \sum_{i=1}^{2}Q_j(z_{i})\frac{P(y_{j},z_{i}\mid \theta )}{Q_j(z_{i})}\label{ex:latentlog2} \\
& \geq \sum_{j=1}^{10} \sum_{i=1}^{2}Q_j(z_{i})log\:\frac{P(y_{j},z_{i}\mid \theta )}{Q_j(z_{i})}\label{ex:latentlog3}
\end{align}
略看一下,好像很复杂,其实很简单,首先是公式 $\eqref{ex:latentlog1}$,这里将 $z_i$ 做为隐藏变量,当 $z_1$ 为结果由硬币 $B$ 抛出,$z_2$ 为结果由硬币C抛出,不难发现:$$\sum_{i=1}^{2}P(y_{j},z_{i}\mid \theta )=P(y_{j}\mid \theta )
=\pi p^{y_{j}}(1-p)^{1-y_{j}}+\pi q^{y_{j}}(1-q)^{1-y_{j}}$$ 接下来公式说明 $\eqref{ex:latentlog1} \Rightarrow \eqref{ex:latentlog2}$ (其中 $\eqref{ex:latentlog2}$ 中 $Q(z)$ 表示的是关于 $z$ 的某种分布,$\sum_iQ_j(z_i)=1$,很直接,在 $P$ 的分子分母同乘以 $Q_(z_i)$。最后是 $\eqref{ex:latentlog2} \Rightarrow \eqref{ex:latentlog3}$,到了这里终于用到了第二节介绍的Jensen不等式,数学好的人可以很快发现,$\sum_{i=1}^2Q_j(z_i)\frac{P(y_j,z_i|\theta)}{Q_j(z_i)}$ 就是 $[\frac{P(y_j,z_i|\theta)}{Q_j(z_i)}]$ 的期望值(如果不懂,可google期望公式并理解),且log是上凸函数,所以就可以利用Jensen不等式得出这个结论。因为我们要让log似然函数 $l(\theta)$最大,那么这里就要使等号成立。根据Jensen不等式可得,要使等号成立,则要使 $\frac{P(y_j,z_i|\theta)}{Q_j(z_i)} =c$ 成立。
再因为$\sum_iQ_j(z_i)=1$,所以得$\sum_iP(y_j,z_i|\theta)=c$,$c$ 为常数,那么(这里感谢网友@无影随想指出错误)$$Q(z_{i})=P(y_{j},z_{i}\mid \theta )/\sum_{i}P(y_{j},z_{i}\mid \theta )
=P(y_{j},z_{i})/P(y_{j}\mid \theta ) =P(z_{i}\mid y_{j},\theta)$$这里可以发现$$Q_j(z_{1}) =\frac{\pi p^{y_{j}}(1-p)^{1-y_{j}}}{\pi p^{y_{j}}(1-p)^{1-y_{j}}+(1-\pi) q^{y_{j}}(1-q)^{1-y_{j}}}\\
Q_j(z_{2} ) =\frac{(1-\pi) q^{y_{j}}(1-q)^{1-y_{j}}}{\pi p^{y_{j}}(1-p)^{1-y_{j}}+(1-\pi) q^{y_{j}}(1-q)^{1-y_{j}}}$$ OK,到这里,可以发现公式 $\eqref{ex:latentlog3}$ 中右边多项式已经不含有“+”符号了,如果知道 $Q(z)$ 的所有值,那么可以容易地进行最大似然估计计算,但是 $Q$ 的计算需要知道 $\theta$ 的值。这样的话,我们是不是可以先对θ进行人为的初始化 $\theta_0$,然后计算出 $Q$ 的所有值 $Q_1$ (在 $\theta_0$ 固定的情况下,可在 $Q_1$ 取到公式 $\eqref{ex:latentlog3}$ 的极大值),然后在对公式 $\eqref{ex:latentlog3}$ 最大似然估计,得出新的 $\theta_1$ 值(在固定Q1的情况下,取到公式 $\eqref{ex:latentlog3}$ 的极大值),这样又可以计算新的 $Q$ 值 $Q_1$,然后依次迭代下去。答案当然是可以。因为 $Q_1$ 是在 $\theta_0$ 的情况下产生的,可以调节公式 $\eqref{ex:latentlog3}$ 中 $\theta$ 值,使公式 $\eqref{ex:latentlog3}$ 的值再次变大,而 $\theta$ 值变了之后有需要调节 $Q$ 使 $\eqref{ex:latentlog3}$ 等号成立,结果又变大,直到收敛(单调有界必收敛),如果到现在还不是很清楚,具体清晰更广义的证明可以见下部分EM算法说明。
另外对公式 $\eqref{ex:latentlog3}$ 进行求偏导等于 $\theta$,求最大值,大家可以自己练习试试,应该很简单的,这里不做过多陈述。
在《统计学习方法》书中,进行两组具体值的计算
- $\pi_0=0.5,\ p_0=0.5,\ q_0=0.5$,迭代结果为 $\pi=0.5,\ p=0.6,\ q=0.5$
- $\pi_0=0.4,\ p_0=0.6,\ q_0=0.7$,迭代结果为 $\pi=0.4064,\ p=0.5368,\ q=0.6432$
两组值的最后结果不相同,这说明EM算法对初始值敏感,选择不同的初值可能会有不同的结果,只能保证参数估计收敛到稳定点。因此实际应用中常用的办法就是选取多组初始值进行迭代计算,然后取结果最好的值。
在进行下部分内容之前,还需说明下一个东西。在上面的举例说明后,其实可以发现上述的解决方法跟一个简单的聚类方法很像,没错,它就是K-means聚类。K-means算法先假定k个中心,然后进行最短距离聚类,之后根据聚类结果重新计算各个聚类的中心点,一次迭代,是不是很像,而且K-means也是初始值敏感,因此其实K-means算法也包含了EM算法思想,只是这边EM算法中用P概率计算,而K-means直接用最短距离计算。所以EM算法可以用于无监督学习。在下一篇文章,我准备写下典型的用EM算法的例子,高斯混合模型(GMM,Gaussian Mixture Model)。
4.EM算法
4.1.模型说明
考虑一个参数估计问题,现有 ${y_1,y_2,…,y_n}$ 共 $n$ 个训练样本,需有多个参数 $\pi$ 去拟合数据,那么这个 $\log$ 似然函数是:$$l(\theta) = \sum_{j=1}^{n} \log P(y_j|\theta)$$ 可能因为 $\theta$ 中多个参数的某种关系(如上述例子中以及高斯混合模型中的3类参数),导致上面的 $\log$ 似然函数无法直接或者用梯度下降法求出最大值时的 $\theta$ 值,那么这时我们需要加入一个隐藏变量 $z$,以达到简化 $l(\theta)$,迭代求解 $l(\theta)$ 极大似然估计的目的。
4.2.EM算法推导
这小节会对EM算法进行具体推导,许多跟上面例子的解法推导是相同的,如果已经懂了,可以加速阅读。首先跟“三硬币模型”一样,加入隐变量 $z$ 后,假设 $Q(z)$ 是关于隐变量 $z$ 的某种分布,那么有如下公式:
\begin{align}
l(\theta)& = \sum_{j=1}^{n}log\: \sum_{i=1}P(y_{j},z_{i}\mid \theta )\label{infer1}\\
& = \sum_{j=1}^{n}log\: \sum_{i=1}Q(z_{i})\frac{P(y_{j},z_{i}\mid \theta )}{Q(z_{i})}\label{infer2}\\
& \geq \sum_{j=1}^{n} \sum_{i=1}Q(z_{i})log\:\frac{P(y_{j},z_{i}\mid \theta )}{Q(z_{i})}\label{infer3}
\end{align} 公式 $\eqref{infer1}$ 是加入隐变量,$\eqref{infer1} \Rightarrow \eqref{infer2}$ 是在基础上分子分母同乘以,$\eqref{infer2} \Rightarrow \eqref{infer3}$ 用到Jensen不等式(跟“三硬币模型”一样),等号成立的条件是,$c$ 是常数。再因为,则有如下 $Q$ 的推导:
\begin{equation*}\sum_{i}P(y_{j},z_{i}\mid \theta )/c=1\\
\Rightarrow \sum_{i}P(y_{j},z_{i}\mid \theta )=c\\
\qquad \qquad \qquad \qquad \Rightarrow Q_{j}(z_{i})=P(y_{j},z_{i}\mid \theta )/\sum_{i}P(y_{j},z_{i}\mid \theta )\\
\qquad \qquad \qquad \qquad \qquad =P(y_{j},z_{i}\mid \theta )/P(y_{j}\mid \theta )\\
\qquad \qquad \qquad =P(z_{i}\mid y_{j},\theta )
\end{equation*} 再一次重复说明,要使 $\eqref{infer3}$ 等式成立,则 $Q_j(z_i)$ 为 $y_j,\ z$的后验概率。算出 $Q_j(z_i)$ 后对 $\eqref{infer3}$ 就可以进行求偏导,以剃度下降法求得 $\theta$ 值,那么又可以计算新 $Q_j(z_i)$ 的值,依次迭代,EM算法就实现了。
EM 算法(1)
选取初始值 $\theta_0$ 初始化 $\theta$,$t=0$
Repeat {
E步:
\begin{equation*}
\begin{split}
Q_{j}^{t}(z_{i})& =P(y_{j},z_{i}\mid \theta^{t} )/\sum_{i}P(y_{j},z_{i}\mid \theta^{t} )\\
& =P(y_{j},z_{i}\mid \theta^{t} )/P(y_{j}\mid \theta^{t} )\\
& =P(z_{i}\mid y_{j},\theta^{t} )
\end{split}
\end{equation*} M步:
\begin{equation*}
\begin{split}
\theta^{t+1}& =arg\: max_{\theta }\: \sum_{j=1}^{n} \sum_{i}Q_{j}^{t}(z_{i})log\:\frac{P(y_{j},z_{i}\mid \theta )}{Q_{j}^{t}(z_{i})}\\
t& =t+1
\end{split}
\end{equation*}}直到收敛
4.3.EM算法收敛性证明
当 $\theta$ 取到 $\theta_t$ 值时,求得$$\theta^{t+1} =arg\: max_{\theta }\: \sum_{j=1}^{n} \sum_{i}Q_{j}^{t}(z_{i})log\:\frac{P(y_{j},z_{i}\mid \theta )}{Q_{j}^{t}(z_{i})}$$那么可得如下不等式:\begin{align}
l(\theta^{t+1} )& = \sum_{j=1}^{n}log\: \sum_{i}Q_{j}^{t}(z_{i})\frac{P(y_{j},z_{i}\mid \theta^{t+1} )}{Q_{j}^{t}(z_{i})}\label{orderProof1}\\
& \geq \sum_{j=1}^{n}\sum_{i}Q_{j}^{t}(z_{i})log\: \frac{P(y_{j},z_{i}\mid \theta^{t+1} )}{Q_{j}^{t}(z_{i})}\label{orderProof2}
\\
& \geq \sum_{j=1}^{n}\sum_{i}Q_{j}^{t}(z_{i})log\: \frac{P(y_{j},z_{i}\mid \theta^{t} )}{Q_{j}^{t}(z_{i})}\label{orderProof3}
\end{align} $\eqref{orderProof1} \Rightarrow \eqref{orderProof2}$是因为Jensen不等式,因为等号成立的条件是 $\theta$ 为 $\theta_t$ 的时候得到的,而现在中的 $\theta$ 值为 $\theta_{t+1}$,所以等号不一定成立,除非 $\theta_{t+1} = \theta_t$,
$\eqref{orderProof2} \Rightarrow \eqref{orderProof3}$ 是因为 $\theta_{t+1}$ 已经使得 $\sum_{j=1}^{n}\sum_{i}Q_{j}^{t}(z_{i})log\: \frac{P(y_{j},z_{i}\mid \theta^{t} )}{Q_{j}^{t}(z_{i})}$ 取得最大值,那必然不会小于 $\eqref{orderProof3}$ 式。
所以 $l(\theta)$ 在迭代下是单调递增的,且很容易看出 $l(\theta)$ 是有上界的 (单调有界收敛) ,则EM算法收敛性得证。
4.4. EM算法E步说明
上述EM算法描述,主要是参考Andrew NG教授的讲义,如果看过李航老师的《统计方法学》,会发现里面的证明以及描述表明上有些许不同,Andrew NG教授的讲义的说明(如上述)将隐藏变量的作用更好的体现出来,更直观,证明也更简单,而《统计方法学》中则将迭代之间θ的变化罗列的更为明确,也更加准确的描述了EM算法字面上的意思:每次迭代包含两步:E步,求期望;M步,求极大化。下面列出《统计方法学》书中的EM算法,与上述略有不同:
EM算法 (1):
选取初始值θ0初始化θ,t=0
Repeat {
E步:
\begin{equation}
\begin{split}
\label{Estep}
H(\theta ,\theta ^{t})& =E_{z}[logP(Y,Z\mid \theta )\mid Y,\theta^{t}]\\
& =\sum_{z}P(Z\mid Y,\theta ^{t})logP(Y,Z\mid \theta )
\end{split}
\end{equation} M步:$$\theta^{t+1} = arg\: max_{\theta } \: H(\theta ,\theta^{t})$$}直到收敛
$\eqref{Estep}$ 式中,$Y={y_1,y_2,…,y_m},\ Z={z_1,z_2,…,z_m}$,不难看出将 $\eqref{infer3}$ 式中两个 $\sum$ 对换,就可以得出 $\eqref{Estep}$ 式,而 $\eqref{Estep}$ 式即是关于分布 $z$ 的一个期望值,而需要求这个期望公式,那么要求出所有的EM算法 (1) 中E步的值,所以两个表明看起来不同的EM算法描述其实是一样的。
5.小结
EM算法的基本思路就已经理清,它计算是含有隐含变量的概率模型参数估计,能使用在一些无监督的聚类方法上。在EM算法总结提出以前就有该算法思想的方法提出,例如HMM中用的Baum-Welch算法就是。
在EM算法的推导过程中,最精妙的一点就是 $\eqref{orderProof1}$ 式中的分子分母同乘以隐变量的一个分布,而套上了Jensen不等式,是EM算法顺利的形成。
6.主要参考文献
[1]:Rabiner L, Juang B. An introduction to hidden markov Models. IEEE ASSP Magazine, January 1986,EM算法原文
[2]:http://v.163.com/special/opencourse/machinelearning.html,Andrew NG教授的公开课中的EM视频
[3]:http://cs229.stanford.edu/materials.html, Andrew NG教授的讲义,非常强大,每一篇都写的非常精炼,易懂
[4]:http://www.cnblogs.com/jerrylead/archive/2011/04/06/2006936.html, 一个将Andrew NG教授的公开课以及讲义理解非常好的博客,并且我许多都是参考他的
[5]:http://blog.csdn.net/abcjennifer/article/details/8170378, 一个浙大研一的女生写的,里面的博客内容非常强大,csdn排名前300,ps:本科就开博客,唉,我的大学四年本科就给了游戏,玩,惭愧哈,导致现在啥都不懂。