100种思维模型之那什均衡思维模型-038

相信很多人都看过《美丽心灵》这部经典影片。这部影片的主人公就是诺贝尔经济学奖获得者约翰 · 纳什。

        几个年轻的学者在酒吧找乐子，百无聊赖之际，一绝世美女突然降临，身边还有4位女性伙伴。学者们的荷尔蒙被迅速燃起，于是他们都跃跃欲试，纷纷准备去找美女搭讪。

        其中一位学者叫纳什，突然说道：你们想过没有，如果大家都去搭讪，一定会吊高那美女的胃口，她可能谁都不搭理。你们又不甘心，总不能没有伴吧，于是走向美女的同伴，可美女的同伴会接受你们吗？她们会说：“走开！人家看不上你，你才来找老娘的！”所以，这种结果就是：大家都没有伴，我们的收益总和最小。

        可是，我们换一种策略，都不去追求那个最美的，而是分别找她的同伴，那样我们成功的概率会大很多，我们几个人的收益总和也最大。

        纳什说完，自己都把自己给惊到了，他意识到自己发现了一个伟大的理论，马上回到宿舍用数学公式证明了这个理论。这个理论的名字就是“纳什均衡”，纳什也因此获得了诺贝尔经济学奖。

在影片的一个经典场景中，纳什说到 “当团队中的每个人都为自己和团队做最好的事时，最好的结果就会到来。” 很多人把这个认为是对著名的纳什均衡的描述，其实这句话刻画的是帕累托最优。但是这并不影响我们对博弈论的一个初步感观。

博弈论

• 定义

博弈论,又称对策论,是使用严谨的数学模型研究冲突对抗条件下最优决策问题的理论,是研究竞争的逻辑和规律的数学分支。即,博弈论是研究决策主体在给定信息结构下如何决策以最大化自己的效用,以及不同决策主体之间的均衡。

• 基本要素

参与人、各参与人的策略集、各参与人的收益函数,是博弈最重要的基本要素

参与博弈的每一个人都知道其他参与者都与他同样理智且掌握同样的知识、理解整个游戏，同时都追求利益最大化且了解他人也是如此。简单来说就是每个人都是利己的且追求利益最大化的。

Game(游戏): 在泛化的场景中，游戏包含了一些参与者、行为和策略以及最终收益。例如拍卖、棋类、政治等。

Players(参与者)：是指参与到游戏中的具有理智的实体。例如拍卖会上的竞价者、玩剪刀-石头-布的玩家、参加竞选的政客。

Payoff(收益)：收益也可以称为奖励，是玩家在参与游戏中会得到的一个结果，可以为正也可以为负。

纳什均衡

对称博弈统治 AI 世界，其中大多数基于 20 世纪最著名的数学理论之一：纳什均衡。纳什均衡以美国数学家 John Forbes Nash 命名。本质上，纳什均衡描述了这样的场景：每个玩家选择一个策略，当一个玩家不改变策略时，没有玩家能从改变策略中获益。

数学定义：在博弈G=﹛S1,…,Sn：u1,…，un﹜中，如果由各个博弈方的各一个策略组成的某个策略组合（s1*,…，sn*）中，任一博弈方i的策略si*，都是对其余博弈方策略的组合（s1*,…s*i-1,s*i+1,…，sn*）的最佳对策，也即ui（s1*,…s*i-1,si*,s*i+1,…，sn*）≥ui（s1*,…s*i-1,sij*,s*i+1,…，sn*）对任意sij∈Si都成立，则称（s1*,…，sn*）为G的一个纳什均衡。

注：博弈论也称Game Theory，一场博弈用G表示，Si表示博弈方i的策略，ui表示收益。因此，纳什均衡的意思是：任何一方采取的策略都是对其余所有方采取策略组合下的最佳对策；当所有其他人都不改变策略时，为了让自己的收益最大，任何一方都不会（或者无法）改变自己的策略，这个时候的策略组合就是一个纳什均衡。

纳什均衡是一个优美且强大的数学模型，它可以解决很多博弈论问题，但在一些对称博弈环境中捉襟见肘。对于初学者而言，纳什方法假设玩家具备无限的计算能力，而现实环境中几乎不存在这种情况。

此外，很多纳什均衡模型无法解释风险概念（常见于大多数非对称博弈场景，如经济市场）。因此，很多非对称博弈场景很难利用纳什均衡实现。在多智能体 AI 系统中这一点尤为重要，这需要在解决方案的数学优雅性和实现的可行性中找到合适的平衡。

​纳什均衡可以认为是博弈论实现人工智能的一个基本基石。它是每一个参与者所选择的一种行为，可使没有参与者会改变这种行为，因为改变会使其不是最优选择；或者说在考虑其他参与者是理智的，也会选择他们的最优策略的情况下，纳什均衡是某参与者的最佳选择。

​在参与者的可选行为集下，他不可能通过改变策略而提高其收益了，我们可以认为纳什均衡的选择是无悔的。

• 经典例子

考虑一下博弈论中最经典的例子：囚徒困境(The Prisoner’s Dilemma )。这个例子解释了在存在共同或互斥利益、共同合作行为的场景下，参与者是如何考虑其个人利益的。

​假设有两个同案犯，Alan和Ben，他们被分开审问，那么有两个选择：保持沉默和认罪。考虑他们两个人的选择的组合有四种：

{沉默，沉默}

{认罪，沉默}

{沉默，认罪}

{认罪，认罪}

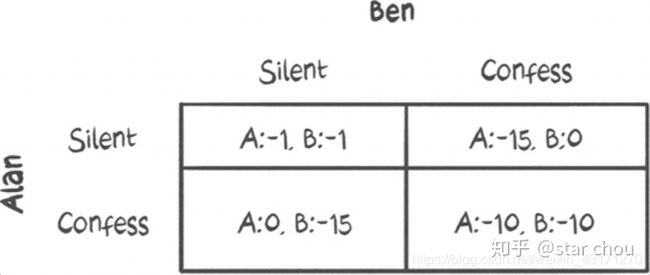
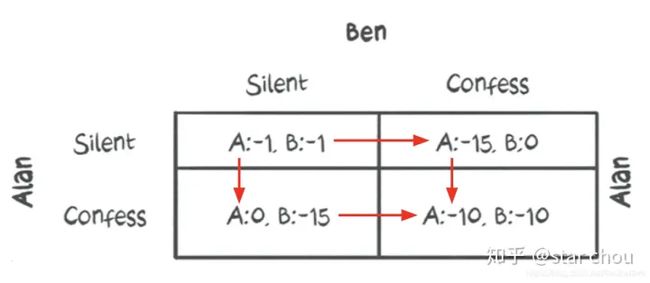
以收益矩阵表示：

上图中的A代表Alan的收益，B代表Ben的收益，负数代表是负收益：

如果两个人都保持沉默，那么每个人都会被判1年监禁。

如果有一个认罪的，将会被转为污点证人而被释放，而另外一个人将会判15年监禁。

如果两个人都认罪，则每个人会判10年监禁。

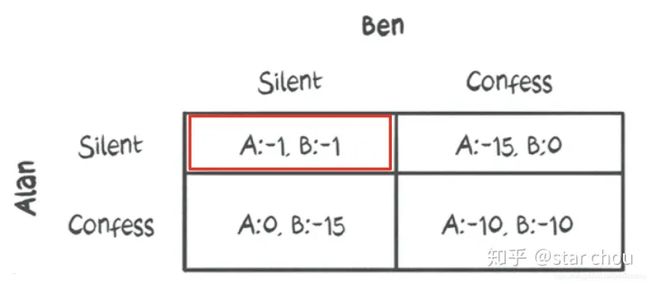
在这种情况下，该如何选择呢？这个困境主要是因为他们都不知道对方的选择会是什么，对于他们来说最优选择显然是上图中的左上角，也就是都保持沉默，这是集体利益是最大化的。

但我们也知道，囚犯会尽力减少他们所受的监禁，这关乎他们的个人利益。即使他们保持沉默，他们仍然会被监禁一年。

实际情况是这样的:

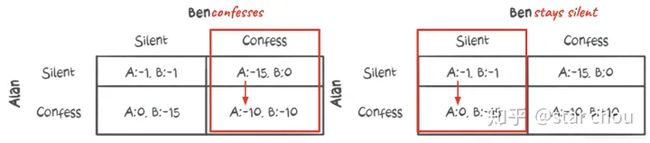
Ben也会这么想。如果我们专注于博弈矩阵，思考过程将会变得非常有趣:

1. 在Ben坦白的情况下，Alan最好的选择就是坦白。这将导致10年的监禁而不是15年
2. 如果Ben保持沉默，Alan最好还是坦白，因为如果他也保持沉默，他将面临一年的监禁，而不是一个自由人

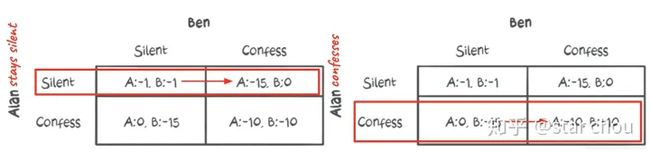
所以这个博弈矩阵和Alan的想法是完全一致的。现在，如果Ben也有同样的想法，博弈矩阵对他来说应该是这样的:

假设Ben也像Alan一样经历了理性思考过程。Ben还得出结论，无论艾伦选择什么，坦白总是有益的。现在，如果我们把这两个囚犯的理性思维叠加起来，结果是这样的:

从结果来看，最好的策略是{坦白，坦白}。即使他们中的任何一个试图偏离这个动作，他们的情况也比他们通过玩这个动作所得到的更糟。因此，{坦白，坦白}是一种纳什均衡策略。

对于纳什均衡，我们可以得出这样的结论:对于任何游戏来说，它都是一个“无悔”的解决方案，但不一定是最优的。

• 纳什均衡分类

纳什均衡可以分成两类：“纯战略纳什均衡”和“混合战略纳什均衡”。

要说明纯战略纳什均衡和混合战略纳什均衡，要先说明纯战略和混合战略。所谓纯战略是提供给玩家要如何进行赛局的一个完整的定义。特别地是，纯战略决定在任何一种情况下要做的移动。战略集合是由玩家能够施行的纯战略所组成的集合。而混合战略是对每个纯战略分配一个机率而形成的战略。混合战略允许玩家随机选择一个纯战略。混合战略博弈均衡中要用概率计算，因为每一种策略都是随机的，达到某一概率时，可以实现支付最优。因为机率是连续的，所以即使战略集合是有限的，也会有无限多个混合战略。

当然，严格来说，每个纯战略都是一个“退化”的混合战略，某一特定纯战略的机率为 1，其他的则为 0。

故“纯战略纳什均衡”，即参与之中的所有玩家都玩纯战略；而相应的“混合战略纳什均衡”，之中至少有一位玩家玩混合战略。并不是每个赛局都会有纯战略纳什均衡，例如“钱币问题”就只有混合战略纳什均衡，而没有纯战略纳什均衡。不过，还是有许多赛局有纯战略纳什均衡（如协调赛局，囚徒困境和猎鹿赛局）。甚至，有些赛局能同时有纯战略和混合战略均衡。