11.人工智能原理-卷积神经网络：图像识别实战

目录

       ​一、卷积运算

       二、池化层

       三、编程实验

       四、总结

       五、往期内容

---

一、卷积运算

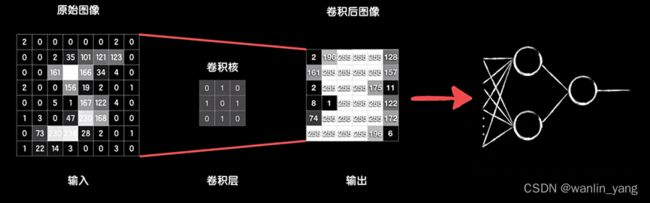
       上节课我们已经了解到卷积操作是怎么一回事，那接下来我们就看看如何把卷积运算融入到我们的神经网络之中。我们还是以上节的“5”为例：

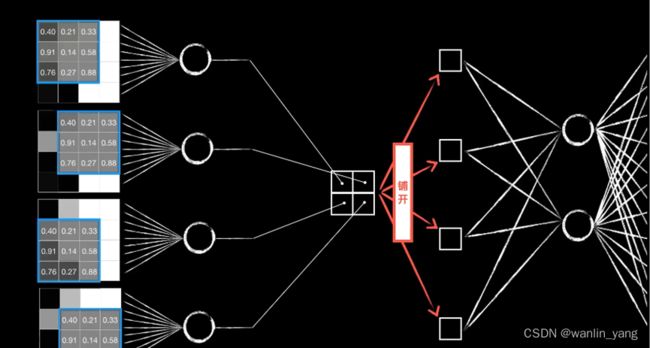
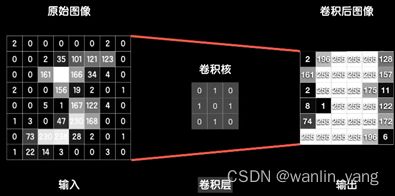
       这是一张8*8的灰度图，用一个3*3的卷积核对它进行卷积，输出一个6*6的结果，我们把这个做卷积运算的一层称为卷积层。卷完以后我们把结果拆成一个数组，送入到后面的全连接层神经网络中。

       那么问题来了，卷积核中的各个值是多少呢？实际上，我们不必管它，随机初始化这些值就好，卷积核的值也是通过训练学习而来的，通过训练找到合适的卷积核去提取不同的特征。

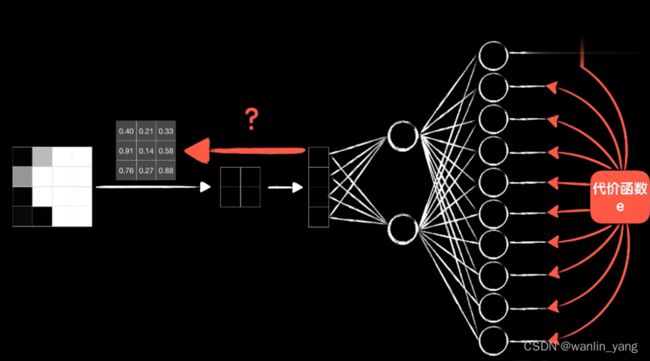
那么如何卷积核反向传播调整参数呢？

       minst数据集是10分类的问题，所以输出层有10个神元。

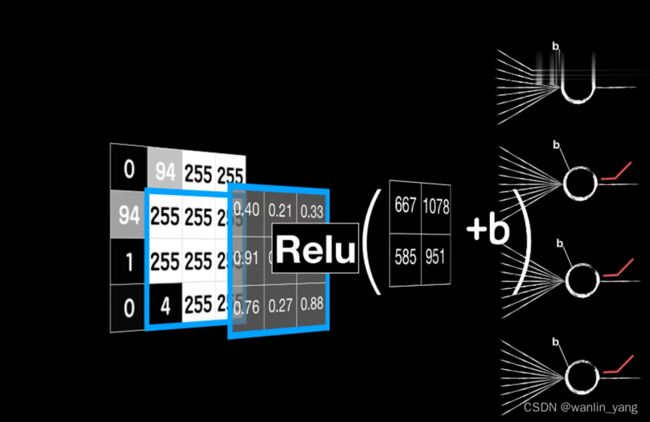
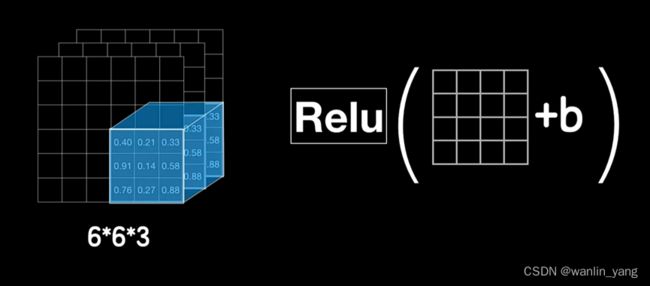
       卷积的过程：卷积核依次和这些小图（局部数据）对应元素相乘再相加得到一个值，可以类比之前讲的普通神经元。神经元的线性函数再加一个偏置项B，然后通过激活函数进行非线性运算，这才是卷积层的最终输出。

       这样我们就把一个卷积层拆成了4个普通的神经元，我们就可以像之前在普通神经元中那样，很轻松地继续把误差代价反向传播下去。

注意以下几个细节：

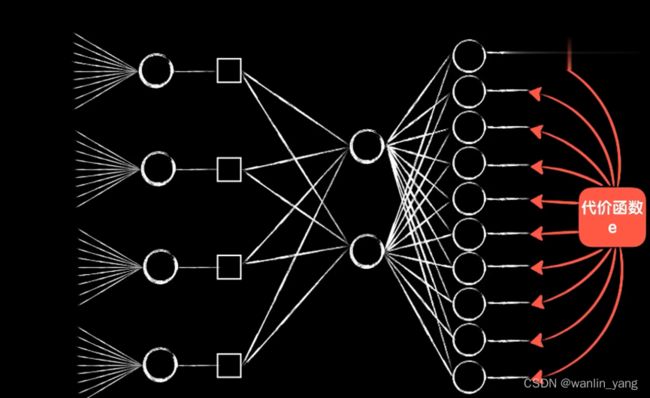
1.首先这四个神经元的输出是根据卷积的过程排列而成的二维的结构，所以我们在送入全连接层时需要手动进行平铺。

2.然后这四个神经元的输入并不相同，实际上是同一个图片的不同区域

3.最后这四个神经元的权值参数并不是独立的，它们都来自同一个卷积核，所以实际上它们的权值参数（包括偏置项b）是一样的，我们只是把一个东西强行拆开平铺成4个。也就是说这四个神经元复用了同一套权重参数，这就是所谓的参数共享。

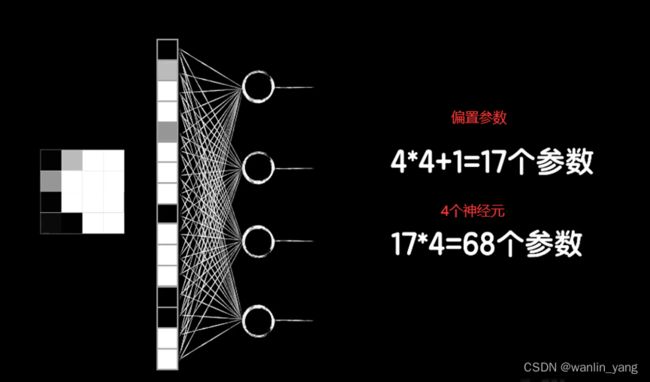
相比之下，如果使用全连接层，需要特别多的参数：

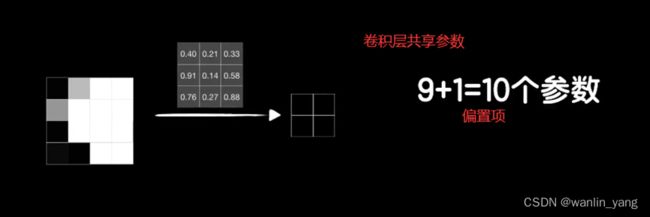
 而卷积层，因为共享参数，只需要10个参数：

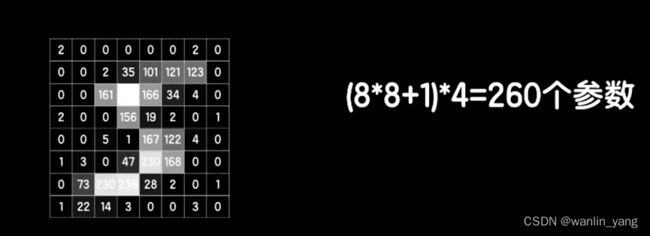
       实际上真实的图片往往比较大，比如8*8的图片，为了得到4个输出，这样的一个全连接层需要260个参数，但如果还是使用3*3的卷积核的卷积层，那么还是只有10个参数。再比如minst的数据集是28*28的图片，需要3140个参数，而如果是我们拍摄的高清大图，那这个参数将变得很大很大，而网络参数越多，也就意味着训练将变得困难和缓慢，但使用3*3卷积核的卷积层还是只需要10个参数。

 为什么卷积核的参数可以共享？

       利用卷积可以提取比如轮廓、纹理这样特征。假如通过训练之后，这个卷积盒变成了一个提取垂直边缘的卷积核，那么一个图像不论是在左上角还是在右下角，还是在其他什么地方，提取垂直边缘的方式都是一样的，所以我们的垂直参数可以共享。所以说卷积核的参数并不是我们事先设置好的，而是像普通神经元的权能参数一样，通过训练学习而来。

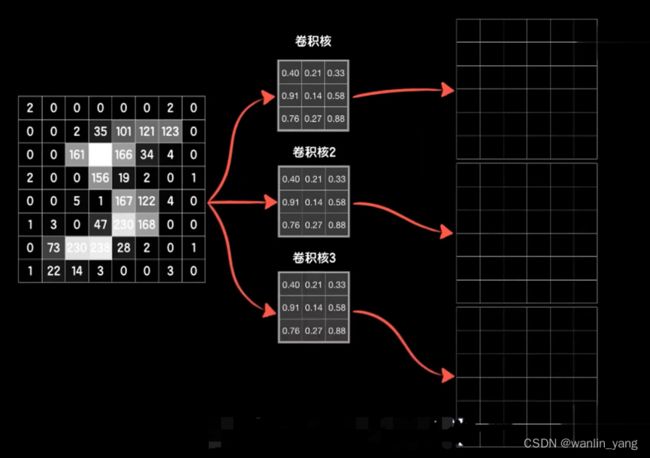
        实际上想要提取多少特征就搞多少卷积核。

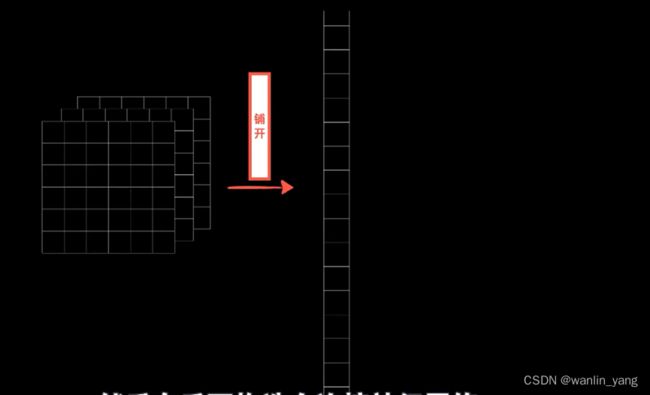
将这3个卷积核卷出来的3个结果（三维的张量）中数据铺开，成为一个一维的向量，然后在后面构造全连接层神经网络，把这个铺平的向量作为数据输入其中。

       但在送入全连接层之前，那我们还能不能继续去卷这个六乘六乘三的数据？

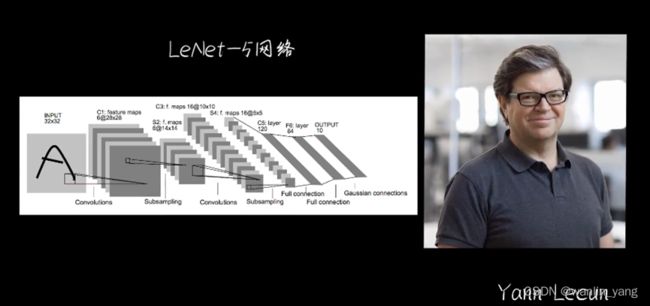
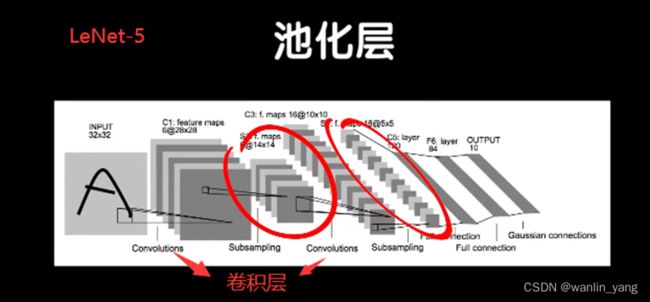
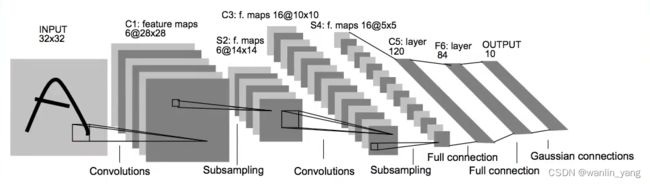
       在卷积网络发展的早期，深度学习领域巨头人物LeCun在1988年提出了一种经典的卷积神经网络结构：LeNet-5，LeNet-5就卷了两次，之后再输入全连接层。

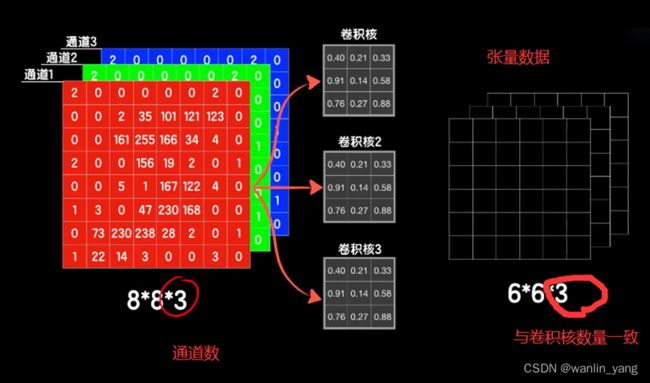
 我们怎么去卷这个六乘六乘三的三维数据？

我们都知道灰度图片是一个通道的，而彩色图片有三个通道的：

此时我们的卷积运算也需要在三维上运算：

二、池化层

可以看出，LeNet-5就卷了两次之后再送入全连接层,里面还多了2个池化层。

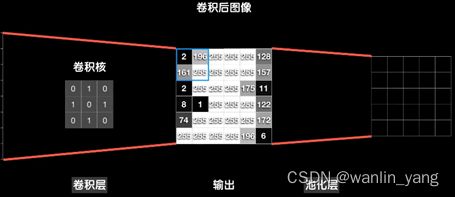
我们从这个数据的左上角开始，框出 2 * 2 区域，相加取平均值，这就是所谓“平均池化” （当然也可以取最大值，称为“最大池化”）

 加入池化层能很好地提取主要特征，在很多经典的卷积神经网络中，往往都会在卷积层之后加上池化层，但这并不是必须的。还有一点，池化操作因为是固定的套路，所以在反向传播中它并没有任何需要学习的参数。

三、编程实验

1.我们简单的复现一下LeNet-5网络：LeNet-5.py

LeNet-5网络

 卷积（32*32变成28*28）

Conv2D(）函数中padding填充模式 ：

 1.卷积-Same模式：

       卷积之前，根据卷积盒的大小，先在原始图像的四周填充几圈全是零的像素点，比如卷积盒是5*5，那么就填充2圈，这样原始图片就从28*28被填充成为了32*32，被5*5的卷积和卷完之后，仍然是28*28，形状保持不变，这种卷积模式，就是"Same模式"。它的名字说明了一切，卷积后和之前是一样的。

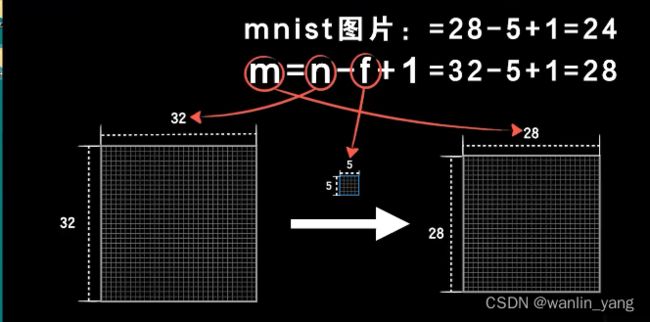
 2.卷积-Valid模式：

       原始图像是28*28的，那被5*5的卷积和卷完之后，就变成24*24的，变小了。那实际上在深度神经网络中，往往有很多层，后面我们发现，卷积层也会有很多层，这就意味着这个原始图像会越卷越小，越卷越小，那随之而来的就是卷完之后信息损失越来越多。

# 导入数据集
from keras.datasets import mnist#导入Keras数据集minst
from keras.models import Sequential #堆叠神经网络序列的载体
from keras.layers import Dense #全连接层，一层神经网络
from keras.optimizers import SGD  #引入keras.optimizers调整学习率
import matplotlib.pyplot as plt #绘图
from keras.utils import to_categorical# one-hot编码转化
from keras.layers import Conv2D# 导入2D卷积层
from keras.layers import AveragePooling2D# 导入二维平均池化层
from keras.layers import Flatten# 数组平铺

(X_train, Y_train), (X_test, Y_test) = mnist.load_data()
# 减少差距，加快梯度下降，归一化操作
# 彩色图片为3通道，这里是28,28,1，代表28*28*1，为1通道的28*28的图片
X_train = X_train.reshape(60000, 28, 28, 1) / 255.0
X_test = X_test.reshape(10000, 28, 28, 1) / 255.0

#把0-9的数值转化为one-hot编码
Y_train = to_categorical(Y_train, 10)
Y_test = to_categorical(Y_test, 10)

#创建堆叠神经网络序列的载体Sequential
model = Sequential()
# 卷积层部分
model.add(
    Conv2D(
        filters=6,  # 卷积核/过滤器数量
        kernel_size=(5, 5),  # 卷积核尺寸，5*5
        strides=(1, 1),  # 步长，向右步长1，向下步长1
        input_shape=(28, 28, 1),  # 输入形状，灰度图形状28*28*1
        padding='valid',  # 填充模式（越卷越小）
        activation='relu'  # 激活函数
    )
)
# 池化窗口大小为 2*2
model.add(AveragePooling2D(pool_size=(2, 2)))#pool_size指定池化窗口大小
# 卷积层部分
model.add(
    Conv2D(
        filters=16,  # 卷积核/过滤器数量
        kernel_size=(5, 5),  # 卷积核尺寸
        strides=(1, 1),  # 步长
        #不再指定input_shape，Keras会自动推断出来， 
        padding='valid',  # 填充模式（越卷越小）
        activation='relu'  # 激活函数
    )
)
# 池化窗口大小为 2*2
model.add(AveragePooling2D(pool_size=(2, 2)))#pool_size指定池化窗口大小

model.add(Flatten())# 数组平铺

# 全连接层部分
model.add(Dense(units=120, activation='relu'))
model.add(Dense(units=84, activation='relu'))
model.add(Dense(units=10, activation='softmax'))#softmax函数做多分类

# 配置模型
model.compile(loss='categorical_crossentropy', optimizer=SGD(lr=0.05), metrics=['accuracy'])
#loss（损失函数、代价函数）：categorical_crossentropy多分类交叉熵代价函数学习率为0.05
# optimizer（优化器）：sgd（随机梯度下降算法）；学习率为0.05
# metrics（评估标准）：accuracy（准确度）；

#训练数据fit， batch_size送入批次的数据，显卡越好，可以送的数据越多，只能用CPU训练，你奶奶就设置小一点
model.fit(X_train, Y_train, epochs=100, batch_size=256)

# 评估测试集
loss, accuracy = model.evaluate(X_test, Y_test)
print("loss" + str(loss))
print("accuracy" + str(accuracy))

 训练结果与测试结果如下：

        最后我们的LeNet-5神经网络在mnist的测试计算的准确率高，达到了98.4%，比上节课的97%要高，而且相比于上节课三层隐藏层，每层256个神经元的全连接神经网络，你可以简单的算一下这个卷积神经网络的参数网实际上要少很多。

四、总结

        本节课介绍了LeNet-5神经网络，它包括了两层卷积层、两层池化层。通过编程实验，我们发现LeNet-5神经网络在mnist的测试计算的准确率高，而且相比于上节课三层隐藏层，LeNet-5神经网络参数网实际上要少很多。当然这还是一个最早期的卷积神经网络结构，那在后期出现的更加复杂的卷经网络，比如AlexNet 、VGG等，在图像识别领域中的效果也越来越好。

五、往期内容

引言：来一场人工智能的奇妙冒险吧~

1.一元一次函数感知器：如何描述直觉

2.方差代价函数：知错

3.梯度下降：能改

4.曲面梯度下降和反向传播：能改

5.激活函数：给机器注入灵魂

6.隐藏层：神经网络为什么working

7.高维空间：机器如何面对越来越复杂的问题

8.初识Keras：轻松完成神经网络模型搭建

9.深度学习：神奇的DeepLearning

10.卷积神经网络：打破图像识别的瓶颈

11. 卷积神经网络：图像识别实战

12.循环：序列依赖问题

13.LSTM网络：自然语言处理实践

14.机器学习：最后一节课也是第一节课

视频链接： https://pan.baidu.com/s/1yIyySjSqXdTob4MsYZuRTQ?pwd=cw6y