机器学习｜正则化｜评估方法｜分类模型性能评价指标｜吴恩达学习笔记
前文回顾：逻辑回归
目录
正则化
过拟合的问题
代价函数
正则化线性回归
正则化的逻辑回归模型
模型评估方法
留出法（hold-out）
交叉验证法（cross-validation）
自助法（bootstrap）
比较总结
分类模型性能评价指标
混淆矩阵
准确度（Accuracy）
精确度（precision）和召回率（Recall，TPR）
精确度和召回率的调和平均（F_score）
假阳性率（FPR）和真阴性率（TFR）
ROC曲线与AUC的值
PR曲线（Precision-recall Curve）
ROC曲线与PR曲线的关系
正则化
过拟合的问题
如何处理过拟合问题？
- 丢弃一些不能帮我们正确预测的特征。可以是手工选择保留哪些特征，或者使用一些模型选择的算法来帮忙。
- 正则化。保留所有的特征，但是减少参数的大小。
代价函数
正则化线性回归
对于线性回归的求解，我们之前推导了两种学习算法：一种基于梯度下降，一种基于正规方程。
正则化的逻辑回归模型
以上参考学习链接：【中英字幕】吴恩达机器学习系列课程，以上对应7.1-7.4
模型评估方法
关于测试集与训练集：
- 将训练集类比为模拟试卷，将测试集类比为正式考试试卷。
- 测试集要尽可能地与训练集互斥（即测试样本尽量不在训练集中出现），显然，正式考试的题在模拟卷里做过，会影响测试结果。
- 测试集和训练集的划分要尽可能地保持数据分布的一致性（避免因数据划分过程中引入额外的偏差而对最终结果产生影响），显然，只有模拟卷的题型和正式考试的题型差不多，刷模拟卷的效果才更好。
留出法（hold-out）
留出法是直接将数据集D划分为两个互斥的集合，其中一个作为训练集S，另一个作为测试集T。模型是从训练集归纳出来的，性能是在测试集上进行评估。
为了保持训练集和测试集数据分布一致，避免额外的误差，我们可以采用分层随机抽样（分层采样），从而保持相同的类分布。
假设数据集D：1000，其中训练集S（70%），测试集T（30%）。若数据集D包含500正例，500反例，那么最终采样的结果是训练集有350正例，350反例，测试集有150正例，150反例。
留出法具有较高的方差。T的评估可能在很大程度上取决于哪些数据点最终出现在训练集中，哪些数据点最终出现在测试集中。且可用于训练的样本较少，因为有些样本被保留用于测试。因此，单独使用留出法得到的估计结果往往不够稳定可靠。为提高性能，在使用留出法时，一般要采用若干次随机划分、重复进行实验评估后取平均值作为留出法的评估结果。
依然存在的限制：
- 留出法没有尽可能多地利用数据进行训练
- 它也无法控制每条记录用于测试和训练的次数
交叉验证法（cross-validation）
最简单的交叉验证（2折交叉）：假设我们把数据分成两个大小相等的子集，我们选择其中一个子集进行训练，另一个进行测试。然后我们交换子集的角色，使之前的训练集称为测试集，反之亦然。最后总误差是通过对两次运行的误差求平均得到。
一般地，k折交叉验证是将数据分成k个大小相等的分区，在每次运行过程中，选择一个分区进行测试，而其余分区则用于训练。这个过程重复k次，以便每个分区恰好用于测试一次。总误差是通过对所有k次运行的误差进行平均得到的。类似于留出法，k折交叉法同样可以重复几次。
k折交叉法的一种特殊情况：设置k=N（即数据集的大小），这就是所谓的留一法（leave-out-out）。每个测试集只包含一条记录。留一法不受划分方式的影响，每个样本都是一个分区。留一法的评估结果往往被认为是比较准确的，不过当数据集比较大的时候，训练m个模型的计算开销难以承受。
自助法（bootstrap）
在自助法中，训练集被替换采样，即已经选择用于训练的数据被返回原始数据集，这样它被重新选中的概率和原来相等。平均而言，一个大小为N的自举样本包含原始数据集中约63.2%的数据。
没有包含在自举样本中的数据作为测试集。
假设数据集D有N个样本，通过抽取返回的方式从数据集D中抽取N个样本，这抽取出的N个样本就是D'。数据集D中有部分样本从来没有被抽到过，那么没被抽到过的这些数据集就作为测试集D-D'，训练集为D'。
自助法可以从相同的原始数据集生成许多不同的训练集，这使得它在数据集小、难以有效划分训练/测试集时很有用。但自助法会改变初始数据集的分布，会引入估计偏差。因此，如果我们有足够的数据，留出法和交叉验证法将被更广泛地使用。
比较总结
分类模型性能评价指标
混淆矩阵
准确度（Accuracy）
对于给定的测试集，模型正确分类的样本数与总样本数之比。
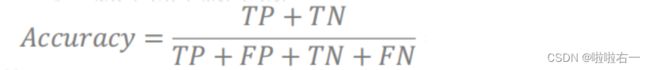更高的准确性并不一定意味着在目标任务上有更好的表现（偏向多数类），它的隐含假设是例子之间的类分布是相对平衡的。
考虑一个二元分类例子：0类示例的数量为9990，1类的数量为10，如果预测全部为0，那准确率也有9990/10000=99.9%，但这显然不正确。
精确度（precision）和召回率（Recall，TPR）
| 精确度 | 召回率 |
| 对于给定测试集，分类模型将正类样本预测为正类的数量与将样本预测为正类的综述的比例。 | 对于给定测试集，模型将正类样本分为正类的数量与模型分类正确的数量的比值。 |
| TP / (TP+FP) | TP / (TP+FN） |
一般来说，精确度和召回率是相互矛盾的衡量标准，Recall↑ → Precision↓，反之亦然，why?
在信息检索中，我们可以认为：
- TP = 实际相关的检索文档
- FP = 实际不相关的检索文档
- TN = 实际不相关的未检索文档
- FN = 实际相关的未检索文档
为了尽可能多地检索相关文档（增加查全率），我们尽可能多地检索文档。最极端的情况是所有的文档都会被检索到，其中所有相关的文档肯定都会被检索到(Recall =1）。然而，精度会相当低。Recall↑ → Precision↓
为了提高精度，我们只检索置信度高的文档，但这样难免会遗漏一些相关的文档，降低查全率。即有Precision↑ → Recall↓
精确度和召回率的调和平均（F_score）
该指标用来综合的衡量模型的召回率和精确度，β是权重因子，当β=1，即为F1_score。
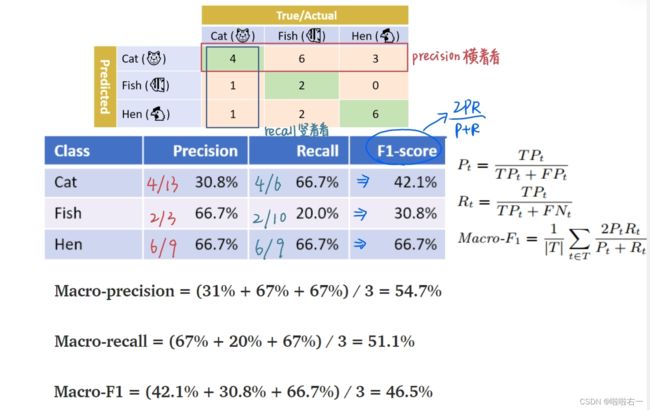
有时我们可能有多个混淆矩阵：重复训练几次；在多个数据集上进行训练；多类或多标签
我们如何评价多类分类的精度和召回率？
假设我们有一组照片。每张照片显示一种动物：猫、鱼或母鸡。我们的分类器需要预测每张照片中显示的是哪种动物。
宏查准率、宏查全率和宏F1
微查准率、微查全率和微F1
假阳性率（FPR）和真阴性率（TFR）
ROC曲线与AUC的值
ROC曲线是衡量分类器性能的一种常见方法。ROC曲线的实际意义在于评估分类器在不同阈值下的真阳性率和假阳性率，以达到最优的分类效果。ROC曲线下面积越接近1，从图中看曲线越接近左上角，说明分类器的性能越好。ROC曲线下面积的值即为AUC值。
设置不同的阈值可以得到不同的混淆矩阵，而每个混淆矩阵又会对应一个TPR、FPR值，在图中对应得到一个点，改变不同的阈值，得到不同的点，最终画出该分类器对应的ROC曲线。
关于分类器阈值以及ROC曲线的实际含义解释，推荐观看该哔哩哔哩视频
- 横坐标为假阳性率——FPR = FP / (TN+FP)
- 纵坐标为真阳性率——TPR = TP / (TP+FN)
PR曲线（Precision-recall Curve）
Precision-Recall Curve可以反映分类器在不同的查全率和查准率条件下的性能表现，评估分类器在不同阈值下的查全率和查准率。通常来说，我们希望分类器在保证尽可能高的查准率的基础上，能够达到较高的查全率。因此，我们可以通过对比不同分类器在同一数据集上的Precision-Recall Curve来选择最优的分类器。曲线越接近右上角，表示分类器的性能越好。
- 横坐标为查全率（召回率，Recall，TPR）——TP / (TP+FN)
- 纵坐标为查准率（精确度，Precision）——TP / (TP+FP)
其中，召回率是指所有真实正样本中被分类器成功预测为正样本的比例，而精确度则是指所有被分类器成功预测为正样本的样本中真正正样本的比例。（详见上文）
ROC曲线与PR曲线的关系
每一个ROC曲线都有唯一的一个PR曲线与之对应，并且如下图，ROC曲线中在左边的那条线对应PR中在上方的那条线。
ROC曲线与PR曲线的适用场景
以下是一个直观的极度不平衡的例子
- 我们可以很明显地看出右边这个图效果是很差的（越靠近右上角的越好），而左边这个图它感觉这个模型效果还是很好的。
- 当预值为0.5的情况，可以得到右上角这样的一个混淆矩阵，它正类是一个都没预测对，尽管是在这么差的情况下，左边的 IOC曲线，看上去分类器效果仍然非常好，而右边这个分类器能够反映出这个模型效果不太好。
所以在这种情况下，我们需要选用 PR曲线，也就是说，如果我们更关心的是正类预测结果，并且给到的数据集非常的不平衡的话，那我们一定要选用PR曲线，而不能选用IOC曲线。
学习视频
机器学习 | 模型评估: ROC曲线与PR曲线(一): ROC曲线与PR曲线的关系
机器学习 | 模型评估: ROC曲线与PR曲线(二): ROC曲线与PR曲线的适用场景
参考博客
深度学习评估方法
常用的分类模型性能评价指标