【Python】一行代码计算两经纬度点的距离及夹角
方法一： 直接调用Python包GeoGraphiclib的函数
2022.2.10更新，Python有现成的包可以直接调用。
geographiclib库
https://pypi.org/project/geographiclib/用法说明见博客：
python 计算地球上两点距离和方位角（bearing）的包geographiclib_梓沂的博客-CSDN博客_geodesic python通过经纬度计算地图上两点的距离及方位角，百度的结果是许多个人写的函数公式，但是python的包那么多，不可能没有这种计算，自建的函数肯定不如公用的包，后来搜到一个https://stackoverflow.com/questions/17624310/geopy-calculating-gps-heading-bearing Use the geographiclib package...https://blog.csdn.net/qq_27361945/article/details/79552213
只需简单两步，就能得到两个经纬度点的距离和方位角。无需劳神补习立体几何。
1. 安装 geographiclib 包
用管理员打开cmd窗口，输入如下命令：
pip install geographiclib2. 调用函数
# -*- coding:utf-8 -*-
# python3代码
from geographiclib.geodesic import Geodesic
# 注意其参数顺序有些奇怪，分别是 点1纬度，点1经度，点2纬度，点2经度
# 北纬和东经为正数，南纬和西经为负数
geodict = Geodesic.WGS84.Inverse(-41.32, 174.81, 40.96, -5.50)
# 距离 float格式
distance = geodict['s12']
# 点1基准方位角
# 方位角是从某点的指北方向线起，依顺时针方向到目标方向线之间的水平夹角
az = geodict['azi1']
# 实测比较准确方法二：自己编写函数实现计算长度及夹角
这部分我参考了下文内容：根据经纬度计算两地距离_weixin_34218890的博客-CSDN博客最近工作需要，网上搜索了下根据经纬度计算两地距离的方法，发现要么是几何法，画图、作一堆辅助线，然后证明推理，要么二话不说直接套公式。这篇文章介绍一种容易理解的方式来求这个距离。0b00 思路地球是个不规则的椭球体、为了简便我们当作球体来计算。 球体上两地的最短距离就是经过两点的大圆的劣弧长度。思路如下:弧长 ← 弦长(两点距离)...https://blog.csdn.net/weixin_34218890/article/details/88740639
原文对原理的阐释非常清晰，浅显易懂该文采用的方法是：将经纬度点转换为三维直角坐标系点，然后根据立体几何知识计算距离。该方法简单清晰，适合精度要求低、距离短的场景。
1 距离计算原理
地球是个不规则的椭球体、为了简便我们当作球体来计算。
球体上两地的最短距离就是经过两点的大圆的劣弧长度。（劣弧，较短的那条弧线）
思路如下:
弧长 ← 弦长(两点距离) ← 两点坐标(直角坐标) ← 经纬度需要具备立体几何知识：
- 圆的角度是360度，用弧度制表示就是 2π 。半个圆的角度是180度，弧度表示是 π。
- 角度与弧度的转换公式：角度 = 弧度 * （180/π) ，弧度 = 角度 * （π / 180）
- 圆弧的角度：圆弧所对的圆心角的角度，一般用弧度值表示其角度。如1/4圆的圆弧，其角度是90度，用弧度表示就是 π/2。
- 圆弧的长度 = 圆弧的角度 * 圆的半径。如半径为2的圆的周长就是 2π * 2 = 4π。
2 距离计算
2.1 坐标转换
设
- 地球半径为 R
- 地心到 E 0° N 0° 的连线为 x 轴
- 地心到 E 90° N 0° 的连线为 y 轴
- 地心到 E 0° N 90° 的连线为 z 轴
- 地球表面有一点 A , 经度为 e , 纬度为 n , 单位为弧度
则 A 的三维坐标可表示为:
2.2 根据坐标计算两点距离
这个太简单，跳过
2.3 根据弦长求弧长
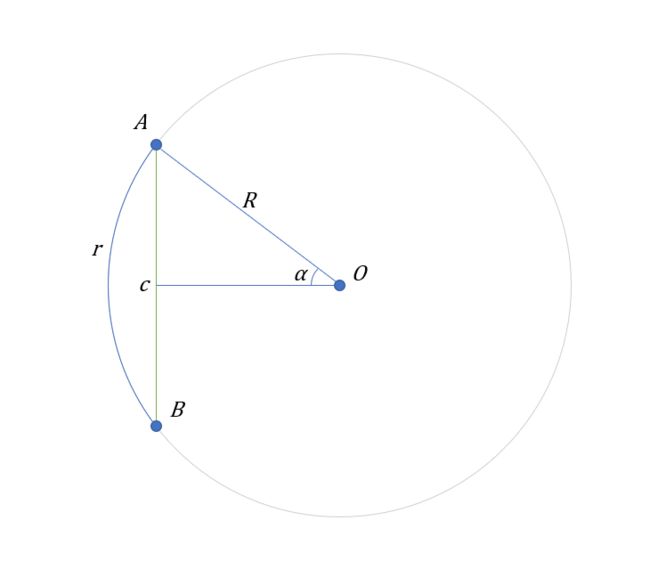
这个可以画个图，帮助理解：
现在已知弦长 c , 半径 R , 要求弧 r 的长度
这很简单, 只需先求出 ∠a （角阿尔法） 的大小 ：
3 距离计算代码
# -*- coding:utf-8 -*-
# python3
import math
def getDistance(e1,n1,e2,n2):
'''
获取两经纬度之间的距离
:param e1: 点1的东经, 单位:角度, 如果是西经则为负
:param n1: 点1的北纬, 单位:角度, 如果是南纬则为负
:param e2:
:param n2:
:return: 两个经纬度间距离，单位千米
'''
R = 6378.137 #地球半径,单位千米
# 将经纬度度数转为弧度
def getPoint(e,n):
e *= math.pi / 180.0
n *= math.pi / 180.0
#这里 R* 被去掉, 相当于先求单位圆上两点的距, 最后会再将这个距离放大 R 倍
return (math.cos(n)*math.cos(e), math.cos(n)*math.sin(e), math.sin(n))
# 计算三维空间的斜边长度
def myHypot(a,b,c):
return math.sqrt(a**2+b**2+c**2)
a = getPoint(e1,n1)
b = getPoint(e2,n2)
c = myHypot(a[0] - b[0], a[1] - b[1], a[2] - b[2])
r = math.asin(c/2)*2*R
return r
d = getDistance(114.123456,30.123456,114.124567,30.123457)
print(d*1000)
4 角度计算原理
计算两个经纬度点的相对角度有很多方法，详查参考资料1。这里只讲其中最简单的一个方法的原理，因为该文只列出公式，未讲解公式原理，我在这里补充说明。
4.1 利用平面直角坐标系法计算两点方位角
适用范围：将经度差和纬度差转化成地面距离再运用平面几何知识求解，所以只能用于短距离求算，中纬度地区建议40km以下。因为计算更简便，所以相对来说有优势。
已知：Aj，Aw，Bj，Bw
当
B点在第一象限及Y轴正半轴，Bearing=A；
B在第二象限，Bearing=360+A；
B在第三四象限及Y轴负半轴，Bearing=180+A。
对于某些系统，再单独设定B位于X正负半轴上的值就可以了，有些系统可以返回arctan（X/0）=90。
4.2 原理说明
数学描述：
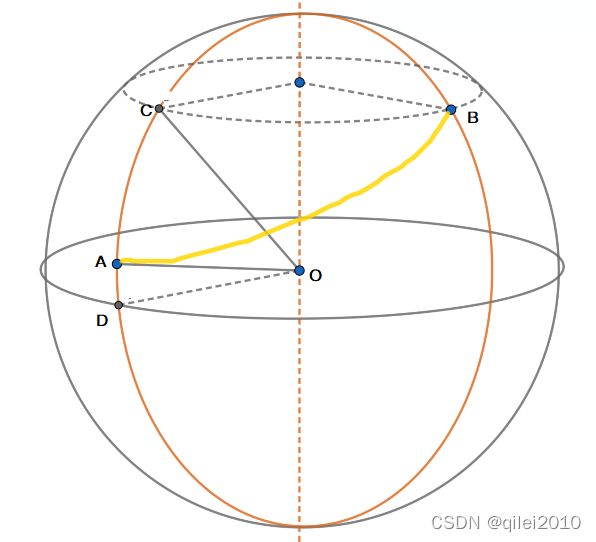
已经起点 A点经纬度（Aj，Aw），终点B点经纬度（Bj，Bw），地球半径为R，求 角CAB，也即 点B 相对点A的方位角。其中，方位角是从某点的指北方向线起，依顺时针方向到目标方向线之间的水平夹角。
问题解答：
当A点B点相距较近的情况下，简单认为 ABC是个平面三角形。∠CAB简写为∠A，弧线BC长度简单写作BC，弧线AC长度简写为AC，则有：
tan∠A = BC / AC
则
∠A = arctan (BC / AC)那么问题就变成，如何求 BC 和 AC。
1) 求AC
这个比较简单，C点与终点B点同纬度，于是 ∠COD 就是 终点B点的纬度值（纬度的定义），∠AOD 就是起点A的纬度值。即
∠COD = Bw
∠AOD = Aw
∠COA = Bw - Aw
AC = R * ( ∠COA * π / 180 )
AC = R * ( (Bw - Aw) * π / 180 )其中，∠COA * π / 180 是为了将 ∠COA 的角度值转为弧度值。
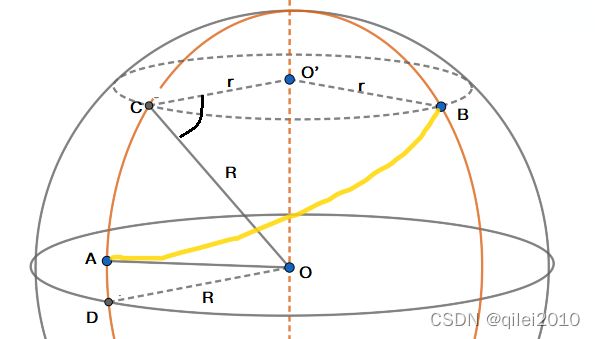
2) 求BC
在CO'B纬度圆即小圆中，BC弧长 = 小圆半径 r × 角CO'B弧度，所以重点是求小圆的半径 r。
根据几何知识，有
r = R * cos∠O'CO
又因 ∠O'CO = ∠COD，其中 ∠COD就是B点 C点的纬度
所以 r = R * cos∠COD = R * cos Bw而∠CO'B 即AB两个点的经度之差：
∠CO'B = Bj-Aj所以，可以得到
BC = r * 角CO'B弧度
BC = r * (Bj-Aj）*π/180
BC = R * cosBw * (Bj-Aj）*π/180 3) 求角A
BC
BC = R * cosBw * (Bj-Aj）*π/180
AC = R * ( (Bw - Aw) * π / 180 )
AC 与 BC 里面都有 R，二者相除约去 R
BC / AC = (Bj-Aj)cosBw / Bw-Aw
∠A = arctan (BC / AC)
∠A = arctan( (Bj-Aj)cosBw / Bw-Aw )于是，得到图片中的公式。
参考资料：
非常全面细致的一篇文章：
[转载]根据两点的经纬度求方位角和距离，等_兔朵朵_新浪博客[转载]根据两点的经纬度求方位角和距离，等_兔朵朵_新浪博客,兔朵朵,http://blog.sina.com.cn/s/blog_5e7960620101vi0d.html