PostgreSQL 技术内幕(六)Greenplum 排序算子
Sort 节点概览
排序的朴素含义是将一个数据集按照某种特定的排序方式进行排列的算法,最常见的排列方式是数值顺序和字典序。
排序算法的应用非常广泛,主要分为了两类:
-
内排序:在内存中完成的排序,常见的有插入排序、快速排序、堆排序、基数排序等。
-
外排序:数据集过大,内存中无法全部存放,需要借助外存的排序,常见的有归并排序的各种变形。
gpdb 的排序节点会根据查询计划中的排序键对指定的元组进行排序,根据排序的数据量和其他的一些性质,gpdb 会选择不同的排序算法:
-
如果排序节点的工作内存可以容纳所有的元组时,排序节点使用快速排序或者堆排序。其中堆排序主要用于 TopK 查询,即只需要输出排序后元组的前 K 个,例如 Sort 节点之上还存在 Limit 节点。
-
如果工作内存无法容纳所有的元组,则使用基于归并排序的外排序算法。
排序节点除了本身对元组排序的功能外,在 gpdb 中的应用也广泛,查询优化器还会根据代价选择基于排序的聚集节点 Group Agg 和连接节点 Merge Join。
此外,Group By,Distinct 等 sql 关键字也和排序息息相关。
TupleSort
TupleSort 是 gpdb 各种排序功能的底层实现,各种需要排序的模块都会调用 TupleSort 对元组进行排序。TupleSort 使用的排序算法如下所示:
| 排序算法 | 状态描述 |
| 快速排序 |
元组集合没有超过内存容量 |
| 堆排序 |
元组集合没有超过内存容量,并且是 TopK 查询 |
| 归并排序(替换选择+多阶段归并) |
元组集合大小超过内存容量 |
其中,快速排序和堆排序都是标准的内存排序算法。
快速排序
快速排序(Quick Sort)是最常见的内存排序算法,由 Tony Hoare 在 1959 年发明。
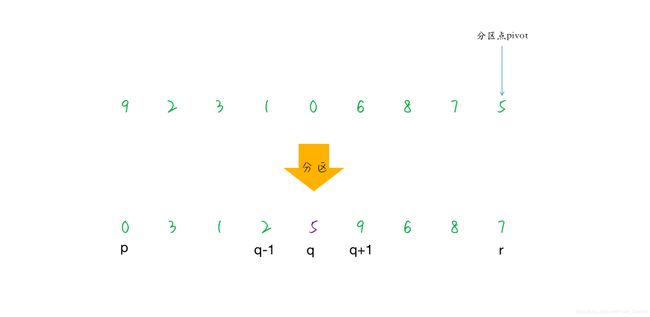
快速排序的三个步骤:首先,挑选基准值,从数据集中挑选出一个基准元素,一般称为 Pivot分割;接着,将所有比 pivot 小的数据放到 pivot 之前,比 pivot 大的数据放到 pivot 之后递归子序列;最后,使用递归将小于 pivot 的子序列和大于 pivot 的子序列分别进行排序。
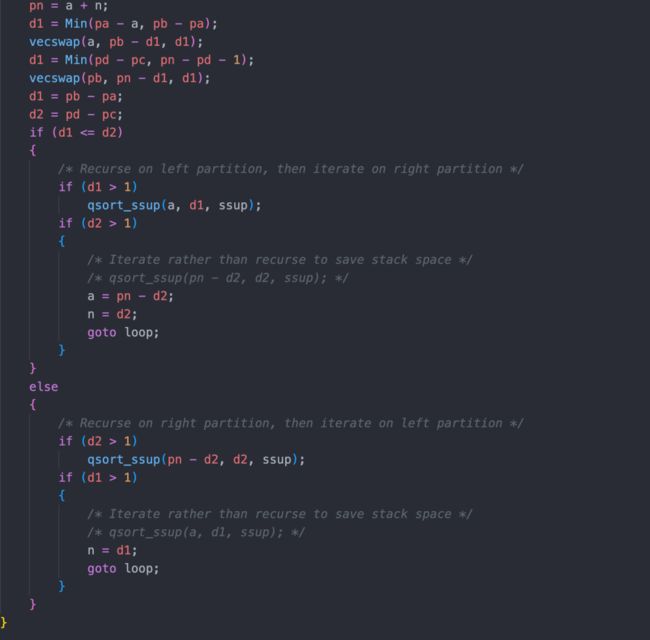
gpdb 中对于快速排序的实现如下:
代码位置:
https://github.com/greenplum-db/gpdb/blob/main/src/backend/utils/sort/gen_qsort_tuple.pl
堆排序
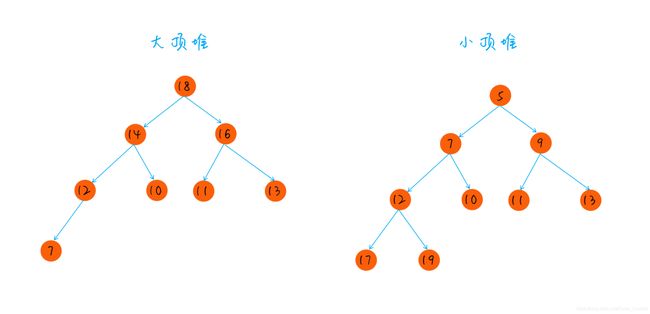
堆排序也是内存中一种常用的排序算法,堆是一种完全二叉树最大堆:对于每个节点,其值大于左右子节点的值最小堆;对于每个节点,其值小于左右子节点的值。
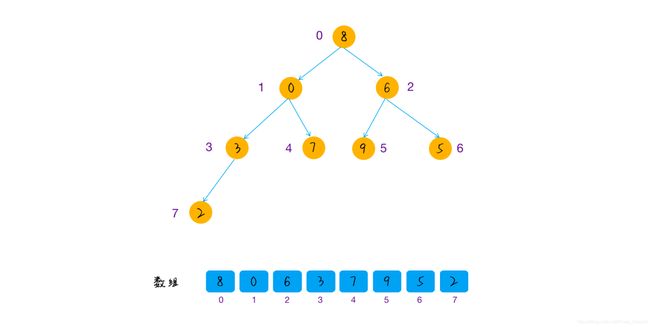
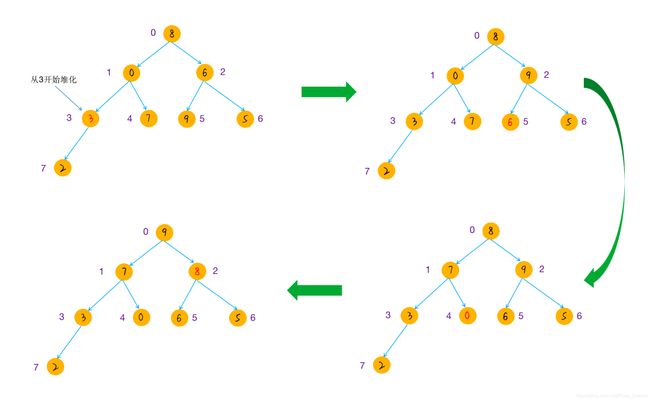
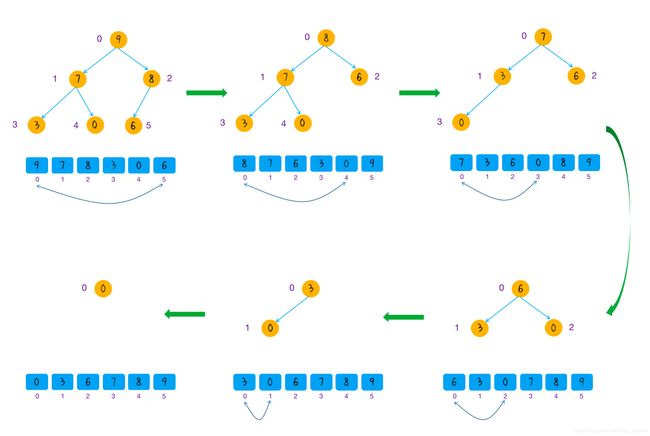
堆排序算法是建立最大堆,数组中的最大元素在堆顶取出堆顶元素,插入到数组中,更新堆重复第二步,直到堆大小为 0原始的数组的排列。示意如下:
开始建堆:
进行排序:
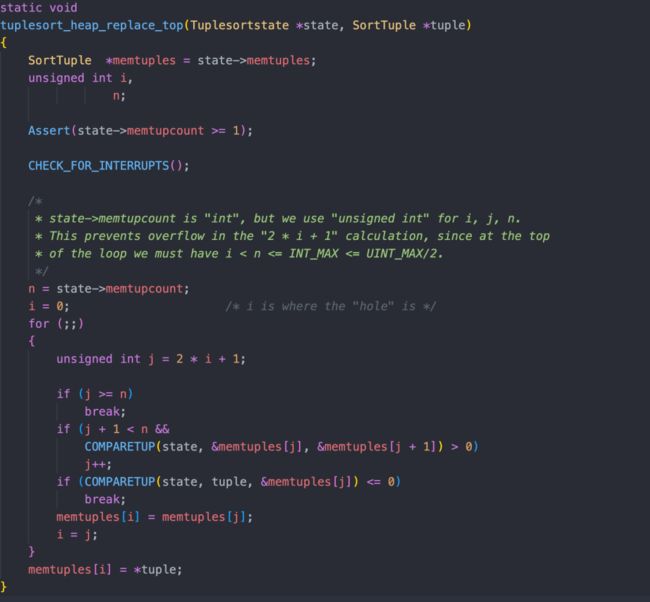
gpdb 中也有对堆排序的实现:
代码位置:
https://github.com/greenplum-db/gpdb/blob/main/src/backend/utils/sort/tuplesort.c#L3525
外部归并排序
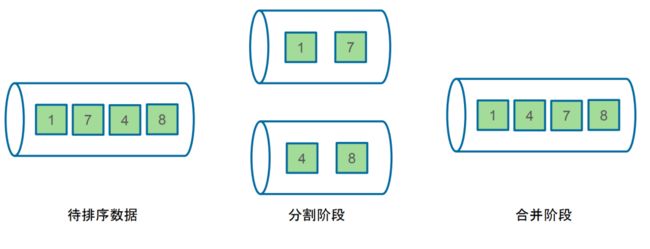
基于外存的归并排序主要分为了两个阶段:
-
分割阶段:将原始待排序数据分成若干个顺串
-
合并阶段:将所有的小顺串合并为包含所有数据的大顺串
顺串的定义:由于要排序的数据集过大,无法全部在内存中排序,因此只能选择部分数据在内存中排序,将排好序的部分数据称为顺串。
替换选择算法分割阶段可以线性扫描一遍数据,当达到内存大小阈值的时候,在内存中排序,生成一个顺串。然后再重复的取出原始数据到内存中排序,生成顺串,直到原始数据被取完。
这样生成的顺串大小,实际上不会超过内存的大小。如果顺串越小,在合并的时候,读取外存的次数就越多,我们的排序算法的效率就越低。
所以,如何在分割阶段 ,尽量生成尽可能大于内存容量的顺串,减少合并阶段读取外存的数量?
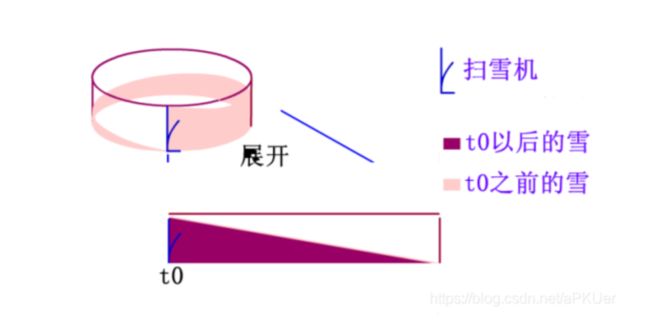
可以使用替换选择算法,替换选择算法借鉴的是扫雪机模型。
想象有一个环形的跑道,跑道上有积雪,假设最开始时积雪的高度为 h,扫雪机不停地向前铲雪,同时也有新的雪落在跑道上,新的雪一部分落在了扫雪机的前面,一部分落在了扫雪机的后面。假设雪下的速度和扫雪机铲雪的速度一致,扫雪机扫了一圈之后,扫雪机前面的高度仍然为 h,后面的高度是 0,这样就达到了一个动态的平衡。
扫雪机前方和后面的积雪就是一个从 0 - h 的斜坡,也就是说路面积雪量就是下图中直角三角形的面积,并且可以计算出扫雪机铲雪的量就是这个三角形的两倍。
类比扫雪机模型,跑道上的积雪就是替换选择算法使用的堆,积雪的量就是内存的大小。
输出当前最小值,生成顺串的过程就是铲雪的过程,顺串的大小就是铲雪量。
新落下的雪就是新的输入数据,由于输入随机,如果输入大于等于刚输出的元素,则被加入到堆中,即被扫雪车清除。如果输入小于刚输出的元素,则相当于新雪下在了扫雪车的后方,本次铲雪(顺串)不包含该元素。
因此,顺串的长度就是铲雪量,也就是内存大小(跑道上的积雪)的两倍。
基于此,替换选择算法的大致过程如下:
-
初始化阶段,将元组读取到内存中,并根据排序键建立最小堆
-
取出堆顶元组,写到顺串文件的缓冲区,并记录这个元组的排序键是 lastkey
-
读取新的元组,如果排序键大于 lastkey,则插入到堆中,重新调整堆的顺序
-
如果新元组的排序键小于 lastkey,则插入到堆的末尾,并将堆的大小减一
-
重复第二步,直至堆的大小变为 0
-
然后重新建堆,再取出新的元组,重复第二步,生成下一个顺串
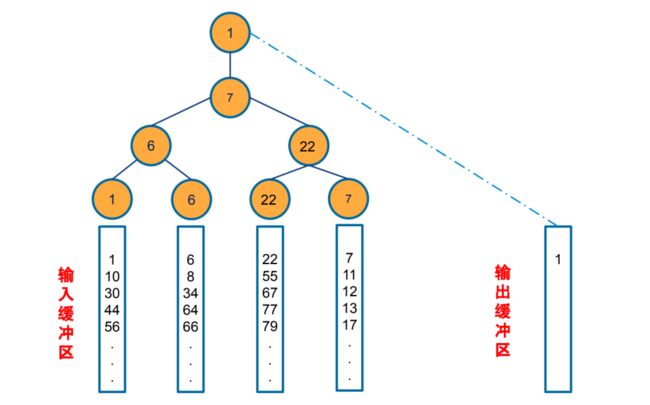
顺串合并假设顺串分布在 K 个文件中,如何高效的比较 K 个文件中的最小值,并将其输出到外部文件中?败者树算法输入每个顺串的第一个记录作为败者树的叶子节点,建立初始化败者树。
两两相比较,父亲节点存储了两个子节点比较的败者(节点较大的值);胜利者 (较小者)可以参与更高层的比赛。这样树的顶端就是当次比较的冠军(最小者)
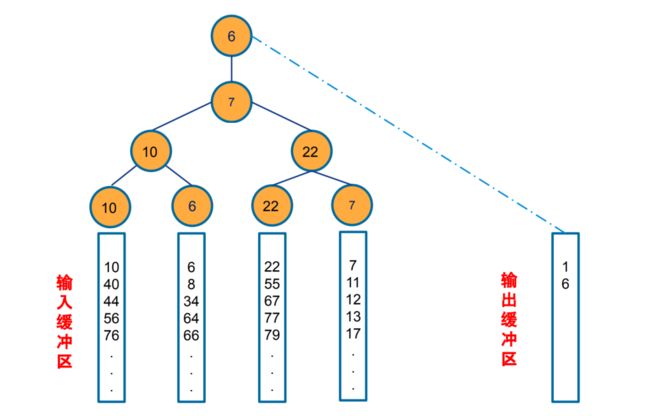
调整败者树,当我们把最小者输入到输出文件以后,需要从相应的顺串取出 一个记录补上去。补回来的时候,我们就需要调整败者树,我们只需要沿着当前 节点的父亲节点一直比较到顶端。比较的规则是与父亲节点比较,胜者可以参与更高层的比较,一直向上,直到根节点。失败者留在当前节点。
第一次比较:
第二次比较:
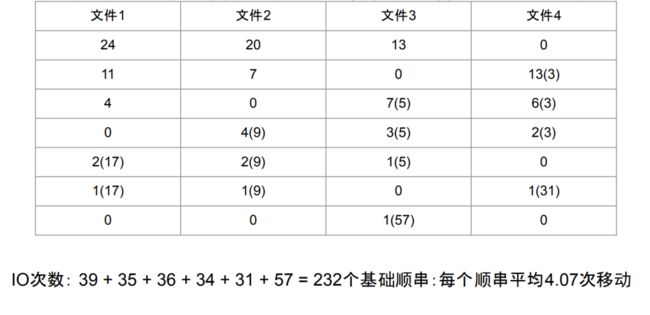
合并阶段如何减少磁盘读取次数多路归并两路归并,使用两个输入文件和两个输出文件,每次归并,顺串的长度翻倍,并存储到输出文件中。下次归并,输出缓冲区和输出缓冲区的位置互换。下面是一个两路归并的例子,每个输入文件在初始状态下有 32 个顺串,每次归并,顺串的长度翻倍。
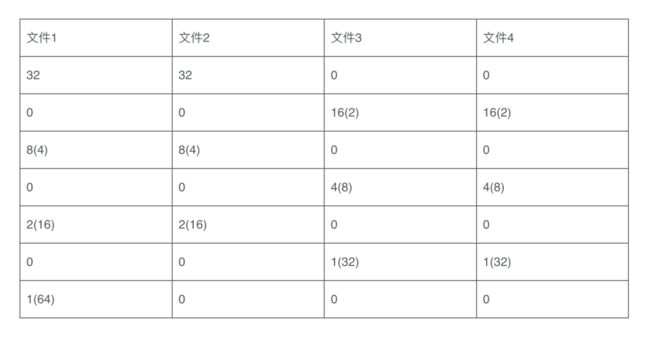
这样归并之后,IO 次数是 64 * 6 = 384 次,每个顺串移动了 6 次,有没有什么更好的办法,可以使顺串的移动次数更少?多相归并Knuth 5.4.2 D 多相归并排序算法。初始化阶段,N+1 个缓冲区,其中 N 个输入缓冲区,1 个输出缓冲区,每一个输入缓冲区包含若干个顺串。
从每个输入缓冲区选取开头的顺串,组成 N 个顺串,并对其进行归并排序,排序结果写入输出缓冲区。此时每个输入缓冲区顺串数减 1,输出缓冲区顺串数加 1。
如果任何一个输入缓冲区的顺串数都大于 0,重复第二步。
如果所有缓冲区的顺串数和大于 1,选择顺串数为 0 的输入缓冲区作为新的输出缓冲区,重复第二步如果所有缓冲区的顺串数和为 1,那么这个顺串就是排序好的数据集,算法结束。
TupleSort 代码逻辑
TupleSort 是排序节点的核心,算法主要分为了四个阶段:第一阶段初始化 TupleSort,调用函数 tuplesort_begin_common,生成 Tuplesortstate,Tuplesortstate 用于描述排序的状态等信息。其中 ,status 字段表示当前状态机的信息。
| 状态 | 状态描述 |
| TSS_INITIAL |
未超出工作内存限制,使用内存数组存储排序元组 |
| TSS_BOUNDED |
触发TopK排序,使用最小值堆存储待排序元组 |
| TSS_BUILDRUNS |
超出工作内存,使用文件存储待排序元组 |
| TSS_SORTEDINMEM |
基于内排序,元组排序完成 |
| TSS_SORTEDONTAPE |
外排序完成,排序后元组存储在文件中 |
| TSS_FINALMERGE |
外排序还差最后一步归并 |
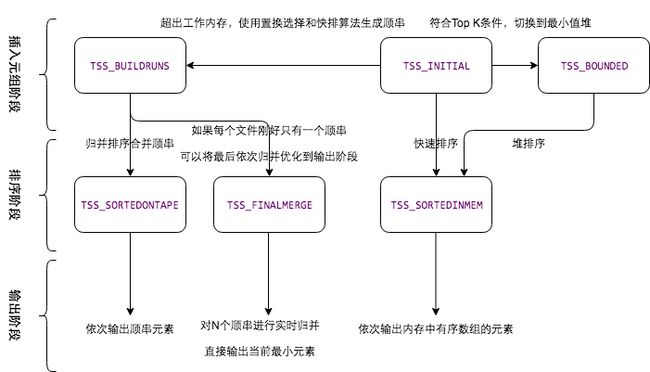
状态转换图:
TupleSortstate 中其他的一些重要字段:
| 类型 | 字段 | 说明 |
| TupSortStatus |
status |
TupleSort状态机当前状态 |
| int |
nKeys |
排序键的个数 |
| bool |
randomAccess |
排序后的元组是否需要随机访问,比如反向读取 |
| bool |
bounded |
是否是TopK查询 |
| int |
bound |
TopK查询中K的值 |
| int64 |
availMem |
节点目前可用内存 |
| int64 |
allowedMem |
节点工作内存 |
| int |
maxTapes |
总缓冲区个数 |
| int |
tapeRange |
输入缓冲区个数 |
第二阶段插入元组,每次调用函数 puttuple_common,根据当前 TupleSortstate 的状态,将元组插入到不同的位置。
-
对于 TSS_INITIAL 状态,会将元组存储到内存的 memtuples 中,如果满足 TopK 的排序条件,会转为堆排序算法,状态切换为 TSS_BOUNDED。
-
TSS_BOUNDED 状态:插入到堆中。
-
TSS_BUILDRUNS 状态:外排序算法,基于替换选择算法,如果元组大于等于堆顶元组,插入当前元组到堆,否则是其他的顺串,将其放到 memtuples 末尾。
第三阶段调用 tuplesort_performsort 执行实际的排序操作,仍然根据状态机,选择不同的排序策略。
-
TSS_INITIAL:所有数据都在内存中,直接执行快速排序,结束后将状态设置为 TSS_SORTEDINMEM
-
TSS_BOUNDED:所有数据仍然在内存中,执行堆排序,结束后将状态设置为 TSS_SORTEDINMEM
-
TSS_BUILDRUNS:执行多相归并排序,函数 mergeruns 负责对顺串进行归并
第四阶段负责输出排序后的元组,在排序完成后,每次调用 tuplesort_gettuple_common 获取排序后的元组。还是会根据不同的状态选择不同的策略。
-
TSS_SORTEDINMEM:元组是在内存中排序的,元组本身也在内存中,直接从 memtuples 中获取即可。
-
TSS_SORTEDONTAPE:元组通过归并排序完成,存储在外部文件中,因此元组需要从文件中读取。
-
TSS_FINALMERGE:元组存储在文件中,每个文件有且仅有一个顺串,在输出元组的时候需要进行合并。
单键排序
gpdb 的排序支持单键和多键排序两种,其中单键排序基于 TupleSort 接口,多键排序基于 TupleSort_mk 接口,排序节点也是标准的执行器三部曲 ExecInitSort、ExecSort、ExecEndSort,但是由于 TupleSort 和 TupleSort_mk 已经封装了完善的排序逻辑,因此三部曲的逻辑就比较简单了。
ExecInitSort
初始化的时候,调用 ExecInitSort 方法,主要负责初始化 SortState 结构体。类型 字段 说明 ScanState
ss
查询状态信息
bool
randomAccess
排序后的元组是否需要随机访问
bool
bounded
是否是TopK查询
int64
bound
TopK查询中K的值
bool
sort_Done
排序步骤是否完成
GenericTupStore*
tuplesortstate
根据排序算法类型,指向Tuplesortstate或者Tuplesortstate_mk
bool
delayEagerFree
某个Segment的排序节点输出最后一条元组后是否可以提前释放内存
ExecSort
ExecSort 负责传递元组给下层节点排序,并将排好序的数据返回给上层节点。ExecSort 的第一次调用会读取所有的元组并传递给 TupleSort 排序。
/** Scan the subplan and feed all the tuples to tuplesort.*/for (;;) { slot = ExecProcNode(outerNode); if (TupIsNull(slot)) break; tuplesort_puttupleslot(tuplesortstate, slot); }SIMPLE_FAULT_INJECTOR("execsort_before_sorting");/** Complete the sort.*/tuplesort_performsort(tuplesortstate);后续每次调用 ExecSort,都会返回排序后的元组。
SO1_printf("ExecSort: %s\n", "retrieving tuple from tuplesort"); /* * Get the first or next tuple from tuplesort. Returns NULL if no more * tuples. Note that we only rely on slot tuple remaining valid until the * next fetch from the tuplesort. */ slot = node->ss.ps.ps_ResultTupleSlot; (void) tuplesort_gettupleslot(tuplesortstate, ScanDirectionIsForward(dir), false, slot, NULL);ExecEndSort
ExecEndSort 的逻辑比较简单,主要就是清理扫描和排序结果,以及清理外排序的临时文件。
/* clean out the tuple table */ ExecClearTuple(node->ss.ss_ScanTupleSlot); /* must drop pointer to sort result tuple */ ExecClearTuple(node->ss.ps.ps_ResultTupleSlot); if (node->tuplesortstate != NULL) { /* * Save stats like in ExecSortExplainEnd, so that we can display * them later in EXPLAIN ANALYZE. */ tuplesort_finalize_stats(node->tuplesortstate, &node->sortstats); if (node->ss.ps.instrument) { node->ss.ps.instrument->workfileCreated = (node->sortstats.spaceType == SORT_SPACE_TYPE_DISK); node->ss.ps.instrument->workmemused = node->sortstats.workmemused; node->ss.ps.instrument->execmemused = node->sortstats.execmemused; } tuplesort_end((Tuplesortstate *) node->tuplesortstate); node->tuplesortstate = NULL; }多键排序
gpdb 中特有的排序方式,针对具有相同前缀的字符串排序的优化。
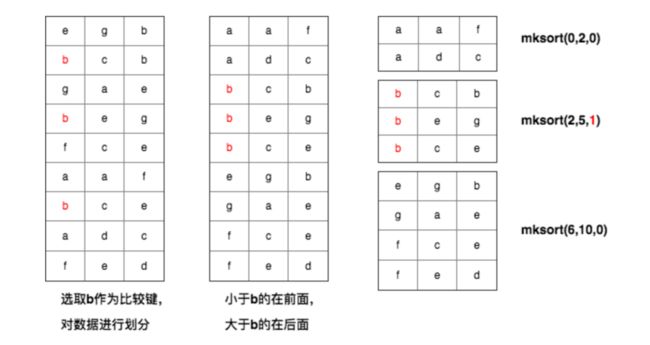
多键排序算法又被称为三路基数排序,融合了快速排序和基数排序的排序算法,主要的优势在于对具有相同前缀的字符串进行更高效的排序。
多键排序的流程和单键排序的三部曲类似,但底层基于 TupleSort_mk 接口。
标准快速排序在处理字符串的时候,平均时间复杂度是 N*logN,当字符串拥有相同的前缀时,快速排序仍然需要花费大量的时间去比较这些字符串的相同前缀,而多键排序避免了对前缀的重复比较,只使用必要的非前缀字符确定排序。
在现实世界中,具有相同前缀的字符串的场景还是很多的,例如很多的 URL 都以 http:// 开头,每个具体的站点都有自己特定的前缀,例如 https://www.baidu.com。
下面是一个多键排序的示例:
注意:从 postgres12 开始,已经自带了多键排序,因此目前 gpdb 当中已经删除了对应的 tuplesort_mk 的逻辑。