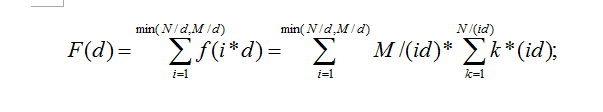acdream 1148 GCD SUM 莫比乌斯反演 ansx,ansy

GCD SUM

Time Limit: 8000/4000MS (Java/Others)Memory Limit: 128000/64000KB (Java/Others)

Submit Statistic Next Problem

Problem Description

给出N,M
执行如下程序：
long long  ans = 0,ansx = 0,ansy = 0;
for(int i = 1; i <= N; i ++)
   for(int j = 1; j <= M; j ++)
       if(gcd(i,j) == 1) ans ++,ansx += i,ansy += j;
cout << ans << " " << ansx << " " << ansy << endl;

Input

多组数据，每行两个数N,M(1 <= N,M <= 100000)。

 

Output

如题所描述，每行输出3个数，ans,ansx,ansy，空格隔开

Sample Input

5 5
1 3

Sample Output

19 55 55
3 3 6

Hint

总数据小于50000

 

对于第一个数字比较容易，用莫比乌斯反演直接就能做。

对于ansx，和ansy是同类问题。现在讨论ansx的做法.

我们设f(d) 代表1<=x<=N,1<=y<=M,gcd(x,y)=d 时，x的求和.

我们设F(d) 代表 1<=x<=N,1<=y<=M,gcd(x,y)为d的倍数时，x的求和

所以F(1) = f(1)+f(2)+f(3)......f(min(N,M))

     F(2) = f(2)+f(4)+f(6)....f(min(N/2,M/2));

     F(i) = f(i)+f(i*2)+f(i*3)....f(min(N/i,M/i));

 

由此我们可得 

由于d = 1 ；所以

对于的反演为

然后可以对mu[i]*i进行筛选，求前N项和。用分块来完成。

代码：

 1 #include<iostream>
 2 #include<stdio.h>
 3 #include<cstring>
 4 #include<cstdlib>
 5 using namespace std;
 6 typedef long long LL;
 7 
 8 const int maxn = 1e5+3;
 9 bool s[maxn];
10 int prime[maxn],len = 0;
11 int mu[maxn];
12 LL hxl [maxn];
13 int sum1[maxn];
14 void  init()
15 {
16     memset(s,true,sizeof(s));
17     mu[1] = 1;
18     for(int i=2;i<maxn;i++)
19     {
20         if(s[i] == true)
21         {
22             prime[++len]  = i;
23             mu[i] = -1;
24         }
25         for(int j=1;j<=len && (long long)prime[j]*i<maxn;j++)
26         {
27             s[i*prime[j]] = false;
28             if(i%prime[j]!=0)
29                 mu[i*prime[j]] = -mu[i];
30             else
31             {
32                 mu[i*prime[j]] = 0;
33                 break;
34             }
35         }
36     }
37     for(int i=1;i<maxn;i++)
38         sum1[i] = sum1[i-1]+mu[i];
39     hxl[1] = mu[1];
40     for(int i=2;i<maxn;i++){
41         hxl[i] = i*mu[i]+hxl[i-1];
42     }
43 }
44 int main()
45 {
46     init();
47     int n,m;
48     while(scanf("%d%d",&n,&m)>0)
49     {
50         LL sum = 0;
51         LL ansi = 0,ansj = 0;
52         int a = n;
53         int b = m;
54         if(a>b) swap(a,b);
55         for(int i=1,la = 0;i<=a;i++,i = la+1)
56         {
57             la = min(a/(a/i),b/(b/i));
58             sum = sum + ((LL)(a/i))*(b/i)*(sum1[la]-sum1[i-1]);
59             ansi = ansi +(hxl[la]-hxl[i-1])*(((LL)(n/i+1)*(n/i))/2)*(m/i);
60             ansj = ansj +(hxl[la]-hxl[i-1])*(((LL)(m/i+1)*(m/i))/2)*(n/i);
61         }
62         printf("%lld %lld %lld\n",sum,ansi,ansj);
63     }
64     return 0;
65 }