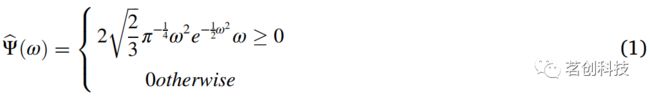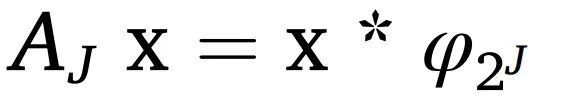小波变换在脑电数据处理中的特征工程

导读

在生物信号中，高效的特征工程和特征提取(FE)是获得最优结果的必要条件。特征可以从时域、频域和时频域三个方面进行提取。时频域特征是最先进的特征，在大多数基于人工智能的信号分析问题中表现良好。本文介绍了小波散射变换(WST)在神经疾病分类中的应用，并对连续小波变换(CWT)和离散小波变换(DWT)在精神分裂症分类中的应用进行了比较研究。本研究是最早将WST应用于脑电数据以分类神经系统疾病的研究之一。本研究在将数据发送给分类器进行分类之前，还从数据中提取了12个统计特征。本研究从核心/传统机器学习(ML)(逻辑回归和支持向量机)和集成学习(EL)(决策树，随机森林，自适应增强和梯度提升)两大类中构建了6种机器学习算法。总共进行了18个实验，研究结果发现，当从CWT和DWT中提取特征时，集成方法表现更好。同时，当从WST中提取特征时，传统ML方法优于EL方法。SVM总体性能较好，但决策树的结果最佳。97.98%，98.2%，97.72%，95.94分别为准确度、灵敏度、特异度和Kappa值，执行时间为48.04s；本研究所提方法的性能优于报道的最先进的方法。

引言

据研究，尽管现有的临床和技术干预措施取得了重大进展，但精神障碍患者的现实生活功能仍有损伤，并且护理需求未得到满足。在神经计算功能的精神保健方面，有许多非侵入性脑成像技术(BIT)可用，例如功能磁共振成像(fMRI)，计算机断层扫描(CT)，正电子发射断层扫描(PET)，脑电图(EEG)和脑磁图(MEG)，功能近红外光谱(fNIRS)等。EEG因其无创、便携、经济、良好的噪声信噪比等特点而成为最好的BIT之一。大脑信号总是由几种基本频率混合而成；根据频率范围或频段的不同，这些信号值大致分为五种类型：delta(1-4Hz)，theta(4-7Hz)，alpha(7-12Hz)，beta(13-30Hz)和gamma(＞30Hz)，这些值可能因研究问题的不同而略有变化。由于不同的频段与不同的疾病相关，因此这些频段在研究各种脑部疾病中起着至关重要的作用。它们被用于测量大脑活动并研究中枢神经系统的结构和功能。本文主要关注从脑电图设备收集的信号。在这里，我们可以看到实时呈现的大脑活动，并且可精确到千分之一秒，同时可以找到电极位置和PSD。

许多研究人员已将脑电信号用于各种脑部疾病的诊断，如精神分裂症(SZ)检测、帕金森病、癫痫发作检测、情绪分类、睡眠障碍，以及脑机接口(BCI)的发展等。本研究致力于对精神分裂症的探索，因为它是全球每300人中就有1人(0.0032%)的主要精神问题之一，这在成年人中更加令人担忧，每222人中就有1人(0.0045%)。这一领域的任何贡献对广大群众都是非常有益的。SZ是一种严重的精神病性神经障碍，SZ患者会出现不同类型的妄想、幻觉、思维障碍、行为紊乱、易激惹等。它可能会导致一种幻觉和高度紊乱的思维，影响日常功能甚至致残。这些人通常在认知或思维能力方面存在困难，比如解决问题和记忆注意力。NIMHANS近年来进行的一项全国心理健康调查(2015-2016)报告称，印度人目前的精神分裂症患病率为0.5%，终身患病率为1.4%。这种疾病的发病主要见于青春期末和二十多岁的人群。SZ患者的死亡时间可能比正常人早2~3倍。这种疾病通常始于青春期晚期或成年早期。精神分裂症与几个关键大脑系统的结构和功能变化有关，包括分别参与工作记忆和陈述性记忆的前额叶和内侧颞叶区域。这种脑部疾病可以通过研究脑成像技术(BIT)来检测和诊断。

特征提取

特征提取是将原始数据转换为可处理的数值特征，同时保留原始数据集中的信息的过程。对于任何基于ML的解决方案，特征提取在获得最佳结果方面起着至关重要的作用，将ML应用于不同神经系统疾病的生物信号也是如此。从数据中选择适当的特征是至关重要的一步，良好的特征提取可以在任何疾病的分类和预测中获得更好的结果。特征表示从模式部分获得的独特属性、可识别的度量和功能组件。提取的特征旨在优化嵌入在信号中的重要信息的丢失。此外，它们还用于降维，从而减少准确描述大量数据所需的计算资源。根据分析和提取特征的领域不同，特征提取方法大致可以分为以下三类：

①时域特征提取

当对信号、数学函数或时间序列数据进行时间分析时，这被称为时域分析。它涵盖了主成分分析(PCA)，线性判别分析(LDA)，独立成分分析(ICA)，经验模态分解(EMD)等技术。

②频域特征提取

在频域方法中，对信号、数学函数或时间序列数据进行频率而不是时间分析。傅里叶变换(FT)、短时傅里叶变换(STFT)、功率谱密度(PSD)、移动平均线(MA)、自回归(AR)、自回归移动平均线等都是频域特征的例子。

③时频域特征提取

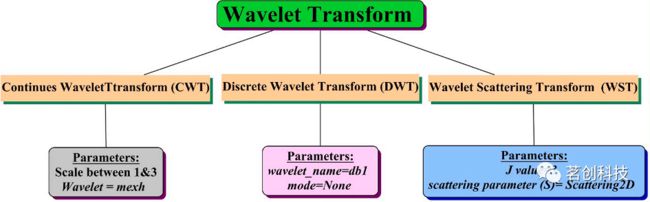
时频域方法将时域和频域方法相结合，克服了时域和频域方法的局限性。时频分析同时涉及时间和频率的信号。时频域分析包括基于频谱图的特征、基于小波分析的特征、短时傅里叶变换等。小波方法是时频域特征提取方法中应用最为广泛的一种方法。小波方法主要有两种类型：连续小波变换（CWT），离散小波变换（DWT），但这些方法有许多变体，WST、FBSE-EWT只是少数几种。

小波方法

小波相较于以往传统方法的主要优势是：WT将复杂的信息片段(如音乐、语音、图像、模式等)分解成不同位置和尺度的基本形式，并对其进行高精度的重建。另外，小波方法在分析非平稳信号方面具有很好的优势，而且小波在时域和频域中都有很好的局域性。WTs具有良好的多分辨率适应能力，非常适合于动态结构信号的分解和去噪。小波变换，将定义在时域的函数映射为具有时间尺度表征的函数。也就是说，小波变换是一维函数的二维表征。小波分析以母小波为中心，母小波是一个基本小波，通常由希腊字母upsilon(ψ)表示。小波函数的能量通常为1。小波变换可以呈现具有良好时间分辨率或频率分辨率的信号。小波变换大致可以分为两种类型：可逆变换和不可逆变换。可逆变换在变换后可以很容易地恢复。不可逆小波是为信号分析而设计的，适用于研究生物医学信号(如EEG、MEG、ECG等)、从传感器测量中检测机械故障，以及研究频率内容如何随时间的变化而变化。与可逆小波变换相比，它需要更多的计算时间。本研究将研究三种类型的小波变换：

①连续小波变换(CWT)

连续小波变换用于将信号分解为小波，这些小波是高度局域性的时间振荡。术语“连续小波”指的是它可以被缩放到任何时间尺度。在傅里叶变换中，信号被分解为无限长的正弦和余弦函数，但此时会丢失时间局域化信息。在CWT中，基函数是时间局域母小波的缩放和平移版本。利用CWT从频率表征中构建良好的时频局域化。CWT是反映非平稳信号变化特性的一种很好的工具。它也是确定信号在全局情况下是平稳还是非平稳的一个出色的工具，当信号被识别为非平稳时，CWT用于查找数据中的平稳段。CWT的墨西哥帽小波函数如下所示。

②离散小波变换(DWT)

离散小波由两个函数组成：缩放函数和小波函数。单位阶跃函数用作缩放函数，小波函数由与单位阶跃函数的偏移量组成。CWT的主要缺点是它会产生大量冗余数据。DWT克服了这一缺点，它通过消除冗余来生成紧凑的数据。Daubechies用Haar小波创建了一个完整的小波家族。与连续小波相比，离散小波仅使用特定的时间尺度进行缩放；缩放通常是2的幂。DWT为信号编码提供了一种有效的工具；它类似于其他离散变换，例如DFT(离散傅立叶变换)或DCT(离散余弦变换)。DWT因其能够给出最优的特征提取结果而被广泛用于许多信号处理领域。Haar小波是离散小波的一种，公式如下：

③小波散射变换(WST)

改进后的时频分析方法是基于小波变换的WST，来自深度学习的卷积神经网络启发了WST设计。小波散射是由小波模块、非线性和低通滤波器级联形成的等效深度卷积网络，以最小配置从实值时间序列和图像数据中得出用于ML和DL应用的低方差特征。WST不需要训练，并且在低数据量下表现较好。WST的优点是不受平移、旋转、缩放、形变的限制，具有丰富的特征信息表征，同时也解决了小波变换随时间变化的缺点。WST的公式如下：

其中*是卷积算子，ψ是母小波(零均值函数)。每个小波ψλ用尺度λ参数化后进行非线性运算|.|，并在2J样本的时域上取平均值，其中

。根据以往文献可以发现，已有研究人员将WST应用于ECG信号，用于对酒精性和非酒精性脑电信号进行分类等。WST也被用于天文学和宇宙学来建立模型，但在医学领域，尤其是在神经科学和EEG方面，它仍然是非常新的。这也是本研究将WST引入EEG信号进行特征提取的动机，并与最流行的小波方法(如CWT和DWT)进行比较研究。研究者选取神经系统疾病精神分裂症来对这些不同的小波方法进行研究。

机器学习算法

机器学习算法在数据中查找模式。这些模式有助于创建一个准确预测的模型。通过更多的数据和训练，可以提高模型的精度。本研究使用传统和集成学习算法来开发ML模型并对疾病进行分类。在集成过程中，将多个模型或算法结合起来以解决特定的计算问题。它大致可分为三类：混合模型、混合组合和混合训练数据。集成学习的两个最重要的技术是：Bagging和Boosting。bagging和boosting之间的主要区别在于这些算法从弱分类器训练的方式。在bagging中，弱分类器是并行训练的，而在boosting中，弱分类器是按顺序训练的。一般来说，当弱分类器表现出高方差时，采用低偏差bagging方法；当弱分类器存在低方差和高偏差时，使用boosting方法。本研究总共创建了六个ML分类器：逻辑回归(LR)、支持向量机(SVM)、决策树(DT)、随机森林(RF)、AdaBoost(AB)、梯度提升(GB)。LR和SVM是传统的ML模型，DT和RF是Bagging模型，AB和GB是Boosting模型。

①逻辑回归(LR)

LR是一种借鉴自统计学领域的分类技术。LR主要用于结果取决于两种可能性或二元(事件是否会发生)的情况。LR还可用于有多项输出的情况，也可以应用于有序结果。逻辑回归有许多优点：实现简单、计算高效、训练效率高、易于正则化。输入特征不需要缩放。

②支持向量机(SVM)

SVM是一种用于执行分类、回归和异常值检测的监督技术。SVM和其他方法的主要区别在于选择决策边界的方式，即最大化与所有类别中最近数据点的距离。SVM可用于线性和非线性分类，采用各种核函数，如齐次多项式、复多项式、高斯径向基函数、双曲正切函数进行非线性分类。

③随机森林(RF)

RF是一个基于树的集成，每棵树都依赖于一组随机变量。RF可用于分类响应变量(分类)和连续响应变量(回归)。随机森林有很多优点：它们可以处理回归和多分类问题，训练和预测速度更快，使用较少的(一个或两个)参数进行调优，易于实现，并且可以直接用于高维问题。

④决策树(DT)

DT可用于分类和回归任务。DT背后的主要思想是创建一个可以预测目标值的模型，对于该模型，DT使用树的表征来解决问题，其中叶节点对应于类标签，属性表示为树的内部节点。

⑤自适应增强(AB)

AdaBoost(自适应增强)背后的核心是使用相同训练数据的加权版本，而不是随机子样本。重复使用相同的训练数据集，使得AdaBoost在小数据集上也能表现良好。这是AdaBoost与已有的boosting算法相比的主要优势。从训练数据中依次得到弱分类器，使用重加权版本的训练数据，其权重主要来自前一个分类器的精度。在为基分类器选择WLs时，必须选择此分类器，这不会减少从之前正确分类的实例中学习到的权重。

⑥梯度提升(GB)

偏差误差和方差误差是机器学习算法中两种广义分类误差；梯度提升使用最小化偏差误差来构建模型。在AdaBoost中，构建模型的人提到了基估计器，而在梯度提升算法中，基估计器是固定的，即决策树桩。梯度提升既可用于连续目标变量(作为回归器)，也可用于分类目标变量(作为分类器)；当使用梯度提升进行回归时，它使用均方误差(MSE)作为代价函数，作为分类器时使用对数损失函数作为代价函数。

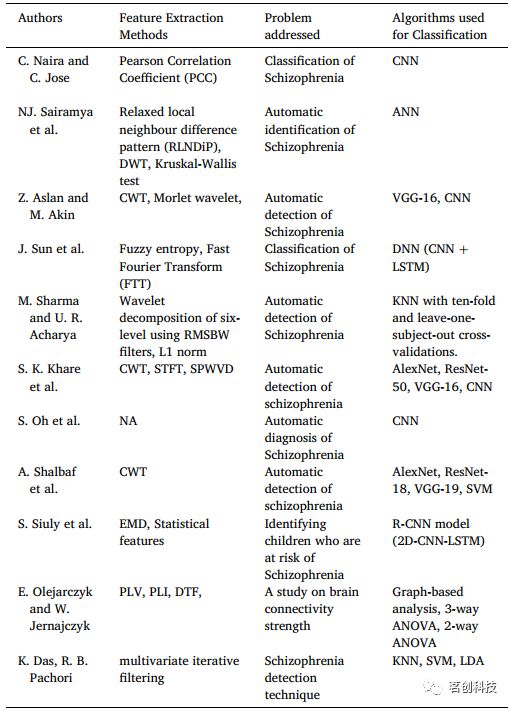
总的来说，本研究应用小波散射变换(WST)从健康对照预测精神分裂症患者，是最早将WST应用于这类数据集的研究之一，据了解，本研究也是最早将WST引入EEG信号以进行神经系统疾病分类的研究之一。本研究在六个ML分类器上对三种不同的小波方法进行了比较研究。在经过详细的文献调查后，尚未发现有应用小波散射变换(WST)的报道。目前的一种小波方法是受卷积神经网络(CNN)的启发，用于分离精神分裂症患者和健康对照组。此次文献调研延伸了人工智能对医疗保健支持、精神分裂症的ML模型和信号处理特征工程的相关研究，并且对小波变换在脑电数据处理中的特征工程非常有针对性。表1给出了各研究人员针对不同问题对脑电信号采用不同特征提取方法的详细情况。

表1.脑电信号相关研究及特征提取方法概览表。

研究方法

本研究以精神分裂症患者为研究对象，构建了脑电信号小波变换特征工程的端到端处理管道。接下来，本研究将详细阐述研究过程中使用的数据集、构建的模型和分类器、进行的实验以及在整个工作中所遵循的方法。实验设计和工作流程如图1所示。

图1.实验设计和工作流程。

数据描述

本研究使用了公开可用的开放数据集，该数据集总共包含28名被试的数据，其中14例为波兰华沙精神病学和神经病学研究所住院的偏执型精神分裂症患者(7名男性：27.9±3.3岁；7名女性：28.3±4.1岁)，以及14名健康对照者(7名男性：26.8±2.9岁；7名女性：28.7±3.4岁)。对照组在性别和年龄上与完成研究的14例患者相匹配。28名被试在闭眼静息状态下共采集了8小时35秒的脑电数据。采用标准的10-20 EEG蒙太奇和19个EEG通道：Fp1、Fp2、F7、F3、Fz、F4、F8、T3、C3、Cz、C4、T4、T5、P3、Pz、P4、T6、O1、O2，采样率为250Hz，FCz为参考电极。图2和图3分别为健康对照和精神分裂症患者所有通道的箱形图，这有助于分析通道及其对信号变化的相应贡献，以便进一步研究。

图2.健康对照信号的通道箱形图。

图3.精神分裂症患者信号的通道箱形图。

预处理

本研究使用python的“mne”库读取数据集中的‘.edf’数据文件，成功读取数据后，使用 mne.Epochs()函数将信号分成epochs。每个epoch为5秒，两个epoch之间有1秒的重叠。对于8小时35秒的脑电数据，本研究从健康对照组中获得了3257500个条目，从精神分裂症患者组获得了3958250个条目。然后，提取了7201个5秒的epoch，每个epoch总共有1250[(250Hz采样频率)×5(秒)]条记录。在epoch之后，从19个通道的数据集中得到了7201个事件，因此得到的NumPy数组的维度是(7201，19，1250)。这些epochs分别使用Pandas和NumPy库转换为数据帧和数组。此外，应用带通滤波滤除信号中的高频噪声，使用0.5Hz的低通频率值和45Hz的高通频率值。应用滤波器去噪前后的脑电信号如图4(a)、(b)和5(a)、(b)所示。

图4.(a)应用带通滤波前健康对照者的信号。(b)应用带通滤波后健康对照者的信号。

图5.(a)应用带通滤波前精神分裂症患者的信号。(b)应用带通滤波后精神分裂症患者的信号。

特征提取

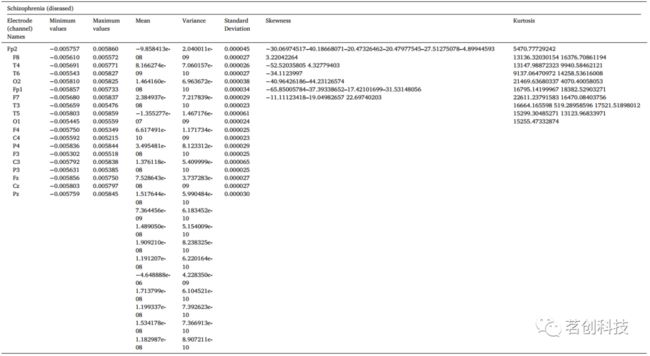
本研究进行了两阶段的特征提取。在第一阶段，提取每个通道的统计特征，如均值、标准差、峰峰值、方差、最小值、最大值、参数最小值、参数最大值、均方根、信号绝对差、峰度和偏度。在第二阶段，采用CWT、DWT和WST三种类型的小波变换来提取小波特征。提取的统计特征如表2(a)和表2(b)所示。然后，将这些特征转换为numpy数组，用于各种ML算法的分类。

表2a.健康对照组的参数分析。

表2b.精神分裂症患者的参数分析。

交叉验证

ML模型的泛化在基于学习的模型中非常重要，为了使本研究开发的模型独立于受试者数据，采用k折交叉验证法，取k值为10。十折交叉验证有助于验证本研究开发的ML模型，并有助于将其推广到其他新数据中。

模型构建

本节完整地描述了已开发的小波变换。讨论了特征提取和本研究为分类构建的六个机器学习模型，以及每个模型和三种小波变换中的不同参数。将已开发的ML模型分为三类：核心/传统ML(逻辑回归和支持向量机)、Bagging模型(决策树和随机森林)和Boosting模型(AdaBoost和梯度提升)。三种小波变换的细节如图6所示。表3提供了使用所有参数建模的六个分类器的详细信息。这些模型是在Scikit-learn库中执行的。

图6.使用参数的小波变换方法。

表3.具有优化参数的ML分类器的模型架构。

评估指标

本研究使用五个指标来评估已开发的分类器：准确度、灵敏度、特异度、kappa分数和执行时间，下面将逐一讨论。

真阳性(TP)：如果分类模型对某一特定情绪的预测结果为阳性，并且实际值也为阳性(正确的特定情绪），则称为真阳性。

真阴性(TN)：如果分类模型对某一特定情绪的预测结果为阴性，并且实际值也是阴性(错误的特定情绪)，则称为真阴性。

假阳性(FP)：如果分类模型对某一特定情绪的预测结果为阳性，但对于该特定情绪的实际值为阴性(错误的特定情绪)，则称为假阳性。

假阴性(FN)：如果分类模型对某一特定情绪的预测结果为阴性(错误的特定情绪)，但实际值为阳性(正确的特定情绪)，则称为假阴性。

准确度：模型的总体精度由以下公式得到

灵敏度(真阳性率)：是指检测结果为阳性的概率，以真阳性为条件，公式如下

特异度(真阴性率)：是指检测结果为阴性的概率，以真阴性为条件，公式如下

科恩的Kappa系数(Kappa分数)：用于衡量定性(分类)项目的两个评分者或评估者之间的一致性程度，公式如下

式中的P0为评估者之间相对观察到的一致性；Pe为假设的机会协议概率。

执行时间：除了矩阵计算之外，本研究还观察到由于转换技术的复杂性，在执行管道时的性能问题。因此，本研究将执行所需的时间视为另一个度量标准，并计算了所有六个模型的执行时间。计算程序的执行时间或运行时间是指执行完整程序而不出错所需的时间。本研究以秒为单位测量了执行时间(执行时间取决于执行时可用的资源、执行时正在运行的进程数量等)。

计算复杂度

计算复杂度是任何模型或算法都应该考虑的最重要的指标之一。它是一个算法所消耗的计算资源的数量。即运行时所需的存储时间和空间。图7给出了已开发的六个ML模型的计算复杂度。

图7.六种已开发的ML算法的计算复杂度。

实验配置

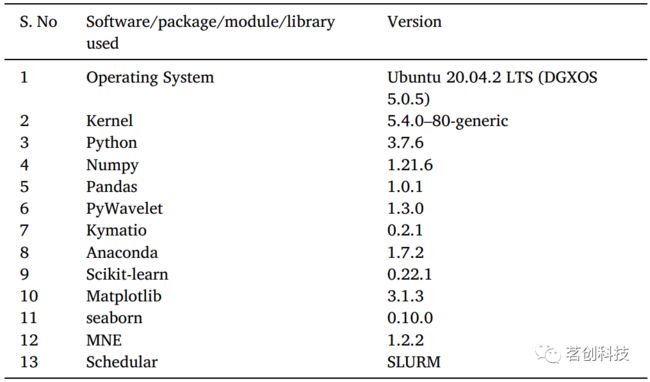
首先，在谷歌Colab上进行实验。在从所有28名被试的数据中创建一个numpy数组后，它生成了一个3.7GB的数组，Colab无法为其分配内存并崩溃。在这里，本研究需要一个具有高计算能力的计算资源来解决这个问题。因此，本研究计划使用印度最快的超级计算机Param Siddhi-AI来执行此实验。所有代码都在Param Siddhi-AI的计算节点上执行，并且仅使用CPU的计算能力。表4(a)中列出了单个计算节点的硬件规格，表4(b)提供了软件、软件包、库等方面的详细信息，以及本研究用于运行实验的版本。

表4a.单个计算节点的硬件规格。

表4b.软件规格。

结果和分析

在这项工作中，研究者在六个AI模型上考察了三种小波变换技术。总共运行了18个机器学习实验[6(2个线性模型+4个集成模型)×3(小波方法)]，并记录了各种性能指标，如准确度、灵敏度、特异度、kappa分数和执行时间。评估指标的详细信息如表5所示。

表5.评估指标的详细信息。

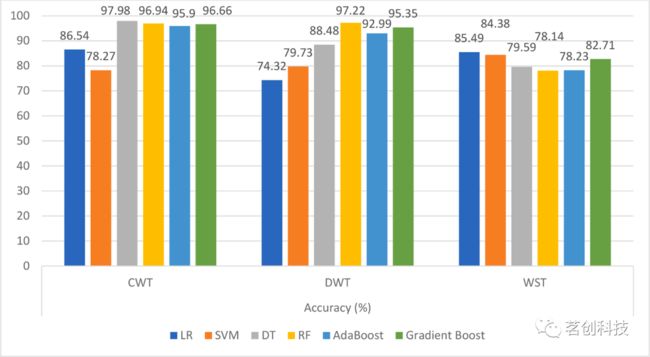
六个ML模型在特征提取后的性能参数如下图所示。准确度、灵敏度、特异度、kappa分数和执行时间的性能参数如图8-12所示。本研究分别计算了所有开发的ML算法的混淆矩阵，并计算了每个开发的ML模型的TN、TP、FN 和FP结果，如下图13-15所示。

图8.六个分类器在三种小波方法下的准确度(%)。

图9.六个分类器在三种小波方法下的灵敏度(%)。

图10.六个分类器在三种小波方法下的特异度(%)。

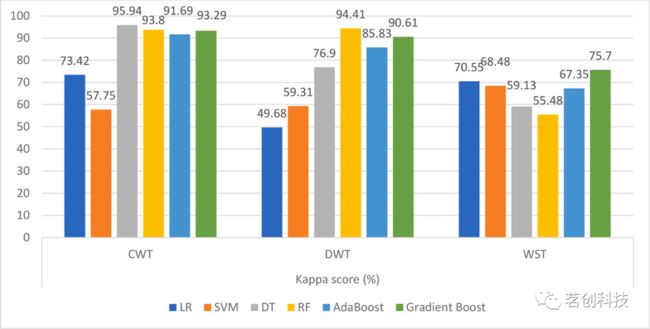
图11.六个分类器在三种小波方法下的Kappa分数。

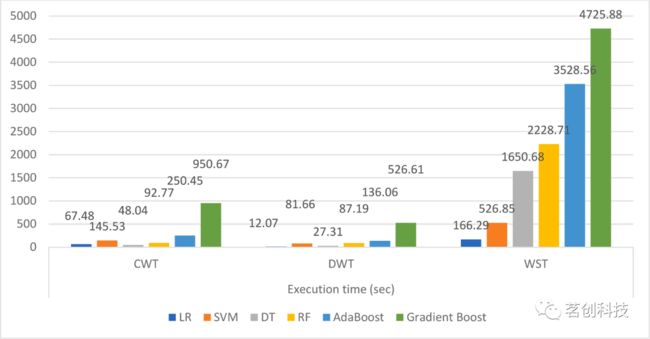
图12.六个分类器在三种小波方法下的执行时间(秒)。

图13.提取CWT和SF后的六个分类器模型的混淆矩阵。

图14.提取DWT和SF后的六个分类器模型的混淆矩阵。

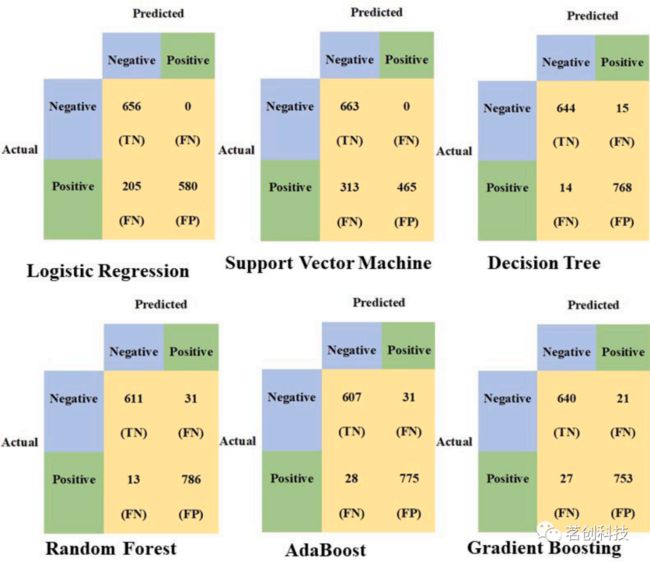
图15.提取WST和SF后的六个分类器模型的混淆矩阵。

结论

在这项工作中，研究者考察了三种不同类型的小波时频特征提取方法以及统计特征提取，并应用了传统、bagging和boosting中六种不同类型的机器学习模型来区分精神分裂症患者与健康对照组。本研究的主要发现是：对于DWT和CWT特征提取方法，集成方法的性能均优于逻辑回归和SVM等核心ML方法。在WST上，核心ML方法的效果优于bagging和boosting方法。核心ML方法的执行时间远小于bagging方法，而bagging方法的执行时间小于boosting技术。在时间-空间复杂度和性能指标方面，DWT特征提取在所有六种分类器中都取得了最好的结果。经过WST特征提取后的ML模型的分类器执行时间是经过CWT和DWT后的分类器执行时间的15~20倍。基于CWT特征提取的决策树ML分类器是18个实验中效果最好的，准确度为97.98%，灵敏度为98.2%，特异度为97.72%，Kappa分数为95.94，执行时间为48.04s。将该开发模型与目前最先进的方法进行比较，取得了更好的效果。

原文：Wavelet transforms for feature engineering in EEG data processing: An application on Schizophrenia.

https://doi.org/10.1016/j.bspc.2023.104811