【动手学因果推断】(二):潜在因果框架
【动手学因果推断】(二):潜在因果框架
- 个人主页:JOJO数据科学
- 个人介绍:统计学top3高校统计学硕士在读
- 如果文章对你有帮助,欢迎✌
关注、点赞、✌收藏、订阅专栏- ✨本文收录于【动手学因果推断】本系列主要记录一些因果推断学习笔记,以及如何应用常见的方法,并给出相关代码,方便大家动手学习,后续会考虑做一些论文总结分析。
潜在因果框架
上一章我们从几个例子介绍了因果推断的一些基本概念,其中我们核心要解决的问题是测量因果效应。接下来我们将正式进入到因果推断的问题研究中。
我们先来看一下一些基本概念
1.潜在结果和个体因果效应(ITE)
首先,潜在结果指的是一个干预后所有可能的结果,我们来考虑两个场景
场景 1 考虑你不开心的场景。你正在考虑是否要养一只狗来帮助你快乐。如果你得到狗后变得快乐,是否意味着狗让你快乐?好吧,如果你没有养狗也会变得快乐怎么办?在那种情况下,狗并不是让你快乐所必需的,所以此时养狗对你的快乐有因果关系的说法是站不住脚的。
场景 2 让我们稍微改变一下。考虑一下,如果你养了一只狗,你很开心,但现在,如果你不养狗,你会变得不开心。在这种情况下,养狗对你是否快乐有因果关系
在上述两种情况下,我们都使用了称为潜在结果概念。
结果Y表示是否快乐: Y = 1 对应于快乐,而 Y = 0 对应于不快乐。你的干预是你是否养狗: T = 1 对应你养狗而T= 0表示不养狗。
我们定义 Y ( 1 ) Y(1) Y(1)表示养狗的潜在结果, Y ( 0 ) Y(0) Y(0)表示不养狗的潜在结果,因此,场景1:
- Y(1) = 1,Y(0) = 1
- Y(1) = 1,Y(0) = 0
更一般地说,潜在结果Y(t) 表示接受干预后的结果会是什么。潜在结果不同于观察到的结果Y,因为并非所有潜在结果都被观察到。在实际中,我们往往只能观察到一个潜在结果。
在我们刚刚的场景中,只有一个个体“你”, 我们定义个人因果效应(ITE):
在刚刚的例子中,场景二的ITE = Y(1)-Y(0) = 1-0=1
现在我们已经介绍了潜在的结果和ITE,我们可以介绍因果推理中出现的主要问题,这些问题在相关或预测的领域中是不存在的。
2. 因果推断的基础问题
核心问题: 我们不可能观察到给定个体的所有潜在结果(missing data!)。
继续考虑养狗的例子。我们无法同时观察到 Y(1) 和 Y(0),除非你有一台时间机器可以让你回到过去并选择第一次没有养狗的版本。你不能简单地得到一只狗,观察 Y(1),把狗送走,然后观察 Y(0),因为第二次观察将受到你在两次观察之间采取的所有行动以及自第一次观察以来发生的任何其他变化的影响观察。
进一步的,因为如果我们不能同时观察到 Y(1) 和 Y(0),那么我们就无法观察到 Y(1) − Y(0) 的因果效应。 这个问题是因果推理所独有的,因为在因果推理中,我们关心的是做出因果推断,而这些推断是根据潜在结果来定义的。相比之下,考虑机器学习。在机器学习中,我们往往只关心预测观察到的结果Y,所以不需要潜在的结果,这意味着机器学习不必处理我们在因果推理中必须处理的这个基本问题。
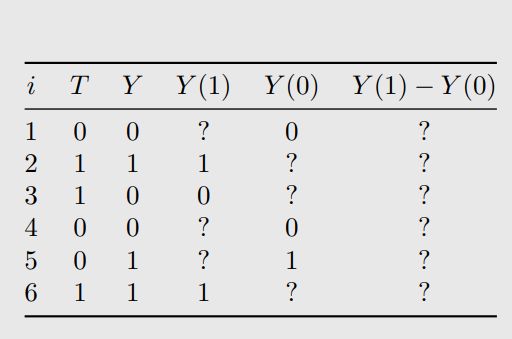
我们称不能观察到的潜在结果为反事实,因为它们与事实结果相反。 观测到的潜在结果被称为事实结果。我们来看下面这个表:
对于每一个个体,我们给予不同的干预 T T T,会得到不同的潜在结果 Y ( t ) Y(t) Y(t),但是要么只能得到Y(1),要么只能得到Y(0),其中?都是我们无法直接得到的。因此这就是我们要解决的问题,处理这些缺失数据
思考 我如何去合理的估算反事实结果,以便于我们因果效应呢?
首先,研究一个个体 Y i ( t ) Y_i(t) Yi(t)可能不是那么有意义,因为这是一个随机变量,我们真正感兴趣的是平均干预效应(Average treatment effect,ATE) A T E = E [ Y ( 1 ) − Y ( 0 ) ] ATE = E[Y(1)-Y(0)] ATE=E[Y(1)−Y(0)]。由期望的线性性质,问题的核心就转化为求 E [ Y ( 1 ) ] − E [ Y ( 0 ) ] E[Y(1)]-E[Y(0)] E[Y(1)]−E[Y(0)]。理想情况下,如果我们能够用不同T取值的条件期望来计算,如下图所示,那就解决了我们的问题,但是,很多情况下,这个等号是不成立的
E [ Y ( 1 ) ] − E [ Y ( 0 ) ] E[Y(1)]-E[Y(0)] E[Y(1)]−E[Y(0)]:描述的是因果关系
E [ Y ∣ T = 1 ] − E [ Y ∣ T = 0 ] E[Y|T=1]-E[Y|T=0] E[Y∣T=1]−E[Y∣T=0]:描述的是相关关系。
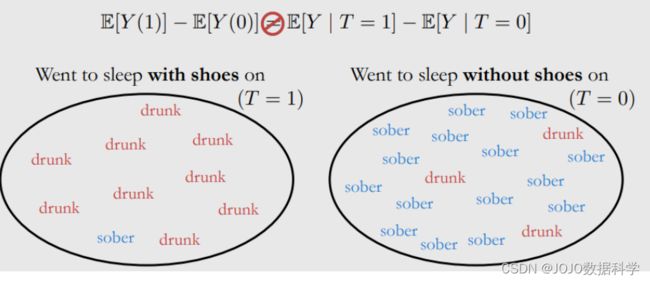
这两者是不等价的,我们上一篇文章举例解释了相关不等于因果。我们再来看一个例子
我们发现穿鞋睡觉与醒来头痛密切相关,但这两者之间没有因果关系
常见原因:前一天晚上喝酒,所以忘记拖鞋,而喝酒又会造成头疼,因此此时是存在Confounding(混淆)变量X(喝酒),它同时造成了穿鞋睡觉和头疼。
还有一种情况是穿鞋睡觉和不穿鞋睡觉的群体是不可比的(样本选择偏差)
我们可以看到,穿鞋睡觉的人大部分是喝醉的,而不穿鞋睡觉的大部分是清醒的,此时样本分布是不一样的,存在选择偏差
那什么时候的可比的呢?
假设穿鞋睡觉和不穿鞋睡觉人群清醒和喝醉的分布是一致的,那么此时就是可比的
接下来我们看一下,在什么假设下,相关和因果是可以划等号的呢?
3. 基本假设
3.1 (Ignorability / Exchangeability)
这个假设是因果推断的关键,因为它允许我们将 ATE退到研究相关差异上。有了这个条件,我们可以计算各个那个例子的因果效应
ignorability:我们可以理解为可以忽略掉混淆变量:在这里就是忽略掉X对T的影响,因此此时不存在confounding(混淆)
从Exchangeability角度来看,交换不同的条件干预,我们的期望是一样的,此时暗示中不同组之间的分布是一致的,不存在样本选择偏差。
因此,这个条件和ignorability是等价的
3.2 Identifiability(可定义的)
Identifiability:我们能够从一个统计学变量中计算因果效应
如果我们能够将因果效应转换到一个统计学变量中,那么我们可以研究它的分布,概率等,进而运用一系列统计方法。
因此,我们在因果推断中,感兴趣都是Identifiability的,这样我们才可以用相关性的方法来研究。
3.3 No interference(无干扰性)
无干扰性:样本i的潜在结果不受其它样本的影响
例如Y代表我是否开心,T表示我是否养狗,那么Y只取决于我是否养狗,而不受其他人是否养狗的影响。
3.4 Consistency(一致性)
当T=t, Y = Y ( t ) Y=Y(t) Y=Y(t),也就是说只有T一样,我们的Y一定也是一样的,否则违背了一致性。例如,假设我养的是金毛,我开心,而我养的柴犬,我不开心,这样就违背了一致性,我们应该要确保无论养什么品种的狗,他们的结果应该是一致的。
3.5 Conditional exchangeability(条件可交换)
首先,我们先引出一个新的概念:条件平均因果效应(CATE)
C A T E = E [ Y ( 1 ) ∣ X ] − E [ Y ( 0 ) ∣ X ] CATE = E[Y(1)|X]-E[Y(0)|X] CATE=E[Y(1)∣X]−E[Y(0)∣X]
此时计算的是在给定一个协变量X的条件下,平均因果效应,和之前一样,我们也需要相应的假设
conditional exchangeability:在给定协变量X的条件下Y与T的独立的
我们刚刚定义的可交换是直接说Y和T独立,忽略X与T之间的关系,那么这里的条件可交换是指在给定X的条件下X和T之间没有关系
注意:条件和独立条件之间没有关系
因此,在满足条件可交换时,我们有以下推导
根据重期望公式,我们可以根据CATE得到ATE:
3.6 Positivity(正向性)
虽然以许多协变量为条件对于实现无混淆很有用,但它实际上可能会带来一些问题。因为没有考虑positivity(正向性)这个条件,正向性是指具有不同协变量的所有数据组都有一定概率接受任何干预的条件。形式上,我们定义二元干预的正向性如下:
为什么需要正向性条件呢?
我们来看求ATE的公式如下
![]()
接下来利用期望的定义:
根据贝叶斯公式:
现在可以看到,我们的分母存在 P ( T = 1 ∣ X = x ) P(T=1|X=x) P(T=1∣X=x),因此要保证它是正值。这就是为什么我们需要正向性假设的数学原理。
直觉上怎么理解呢?
如果违反了正向性假设,那就意味着在数据的某个子组中,每个人总是接受干预或每个人总是接受控制。能够估计该组中实验与对照组的因果关系是没有意义的,因为我们只看到实验或对照组,无法对比。
正向性的另一个名称是重叠(overlap)。这个名字的直觉是我们希望实验组的协变量分布与对照组的协变量分布重叠。
我们可以发现Positivity和unconfoundness存在trade-off的关系
3.7 总结
我们首先引入了无混淆性(条件可交换性),因为它是主要的因果假设。然而,所有的假设都是必要的
- Identifiability (Assumption 2.2)
- No interference (Assumption 2.3)
- Consistency (Assumption 2.4)
- Positivity (Assumption 2.6)
现在我们结合上述的条件,可以将一个因果量转换为统计量
4.因果估计量
为了方便后续相关描述,我们给出几个概念
- estimand: 估计量
- estimate:估计
- estimation:估计过程
其中,我们定义causal estimand为因果估计量,例如 E [ Y ( 1 ) ] − E [ Y ( 0 ) ] E[Y(1)]-E[Y(0)] E[Y(1)]−E[Y(0)]就是一个因果估计量,statistic estimand为统计估计量,例如 E [ Y ∣ T = 1 ] − E [ ( Y ∣ T = 1 ) ] E[Y|T=1]-E[(Y|T=1)] E[Y∣T=1]−E[(Y∣T=1)]是一个统计估计量,我们需要做的是去估计这些统计估计量,然后得到我们的因果关系。
具体怎么估计统计估计量,我们可以运用统计学、机器学习等方法,下面我们来看一个简单的例子
5.实际案例:钠摄入量对血压的影响
这是一个重要的应用,因为发现大约 46% 的美国人患有高血压,而高血压与死亡率有关,如果我们能够发现钠的摄入量与血压是有因果关系的,那么我们就可以控制钠摄入量,实现血压的控制
- Y:血压
- T:T=1表示钠摄入量高于3.5g,T=0表示钠摄入量低于3.5g
- X:协变量,包含年龄和尿液蛋白质含量
现在,我们如何估计ATE呢?,首先,我们假设满足consistency,positivity,条件可交换。然后,我们可以得到ATE:
E X [ E [ Y ∣ T = 1 , X ] − E [ Y ∣ T = 0 , X ] ] E_X[E[Y|T=1,X]-E[Y|T=0,X]] EX[E[Y∣T=1,X]−E[Y∣T=0,X]]
然后,我们将对X的外部期望替换为对数据的平均值,得到以下结果
如何估计内部的条件期望呢?这里有很多机器学习或统计方法应用,我们在这里介绍简单的线性回归。下面来看具体代码和结果
5.1代码
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression
# 数据生成
def generate_data(n=1000, seed=0, beta1=1.05, alpha1=0.4, alpha2=0.3, binary_treatment=True, binary_cutoff=3.5):
np.random.seed(seed)
age = np.random.normal(65, 5, n)
sodium = age / 18 + np.random.normal(size=n)
if binary_treatment:
if binary_cutoff is None:
binary_cutoff = sodium.mean()
sodium = (sodium > binary_cutoff).astype(int)
blood_pressure = beta1 * sodium + 2 * age + np.random.normal(size=n)
proteinuria = alpha1 * sodium + alpha2 * blood_pressure + np.random.normal(size=n)
hypertension = (blood_pressure >= 140).astype(int) # not used, but could be used for binary outcomes
return pd.DataFrame({'blood_pressure': blood_pressure, 'sodium': sodium,
'age': age, 'proteinuria': proteinuria})
df = generate_data()
df.head()
| blood_pressure | sodium | age | proteinuria | |
|---|---|---|---|---|
| 0 | 147.157602 | 1 | 73.820262 | 46.140554 |
| 1 | 133.339602 | 1 | 67.000786 | 40.970603 |
| 2 | 139.833515 | 0 | 69.893690 | 41.835567 |
| 3 | 152.500558 | 1 | 76.204466 | 46.401798 |
| 4 | 149.644768 | 1 | 74.337790 | 44.082575 |
因为这里我们使用的是模拟数据集,我们知道,在这里真实的sodium的效应是1.05
# 计算因果效应
def estimate_causal_effect(Xt, y, model=LinearRegression(), treatment_idx=0):
model.fit(Xt, y)
Xt1 = pd.DataFrame.copy(Xt)
Xt1[Xt.columns[treatment_idx]] = 1
Xt0 = pd.DataFrame.copy(Xt)
Xt0[Xt.columns[treatment_idx]] = 0
return (model.predict(Xt1) - model.predict(Xt0)).mean()
X t X_t Xt是你要输入的干预变量和协变量,y是我们的目标变量。
不加入协变量
不加入协变量我们就只考虑
E [ Y ∣ T = 1 ] − E [ Y ∣ T = 0 ] E[Y|T=1]-E[Y|T=0] E[Y∣T=1]−E[Y∣T=0]
estimate_causal_effect(df[['sodium']], df['blood_pressure'], treatment_idx=0)
4.923220185643586
计算的结果为4.9,和目标的1.05差距很大 ( 4.9 − 1.05 ) / 1.05 = 368.87 % (4.9-1.05)/1.05 =368.87\% (4.9−1.05)/1.05=368.87%.因为我们知道真实的Y还受到X的影响,这个时候直接计算Y对T的条件期望误差是较大的
加入协变量
此时我们要计算的就是
E X [ E [ Y ∣ T = 1 , X ] − E [ Y ∣ T = 0 , X ] ] E_X[E[Y|T=1,X]-E[Y|T=0,X]] EX[E[Y∣T=1,X]−E[Y∣T=0,X]]
estimate_causal_effect(df[['sodium', 'age', 'proteinuria']], df['blood_pressure'], treatment_idx=0)
0.9282888903232163
计算的结果为0.93,和目标的1.05差距较小 ∣ 0.93 − 1.05 ∣ / 1.05 = 11.42 % |0.93-1.05|/1.05 =11.42\% ∣0.93−1.05∣/1.05=11.42%。这一部分误差我们可以认为是随机误差,增大样本量可以减少
总结
我们介绍了潜在结果框架,其中因果推断的核心问题:不能观察到所有的潜在结果,导致我们无法衡量因果效应:ATE 和 CATE
解决方法:将因果估计量退到统计估计量来研究,进而可以应用一系列的统计学和机器学习方法。因此,我们引出了一系列假设,来确保这样做是合理的。
最后我们通过一个模拟数据集,展示了如何计算因果效应,以及是否使用协变量是有较大差异的。
改进: 最后我们使用的是线性回归来估计条件期望, Y = α T + β X Y=\alpha T+\beta X Y=αT+βX,可以看出,不同的X我们的 α \alpha α都是一样的,因此无法捕捉到不同X条件下干预T的异质性,可以考虑使用一些更复杂的非线性模型,后续在进行相关讨论。此外,我们这些假设条件很多情况下可能不成立,那我们该如何进行研究?大家可以思考一下这些问题并进行改进。





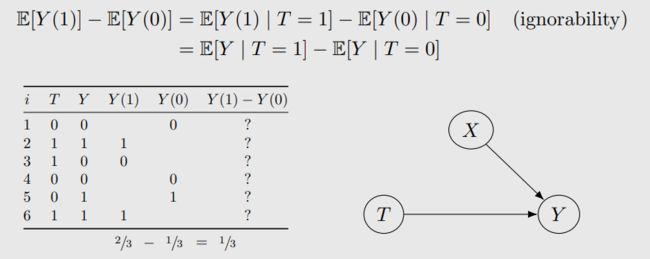







![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-1VjxoQPg-1680086952518)(upload/image-20230329123540110.png)]](http://img.e-com-net.com/image/info8/99179fc3cbea48dab64da48e75e5debd.jpg)



![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-vTNFsRI3-1680086952522)(upload/image-20230329135828319.png)]](http://img.e-com-net.com/image/info8/30e79b64287742219d480cd4b0b9d75c.jpg)