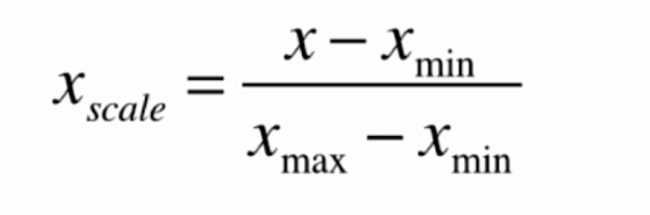keras之分类问题和回归问题

keras之分类问题和回归问题

一、keras之分类问题

• 分类问题预测的是类别，模型的输出是概率分布

• 三分类问题输出例子：[0.2, 0.7, 0.1]

(假设数组中的3个索引位置表示不同类别的概率输出，0.2表示猫类，0.7表示狗类，0.1表示狼类，队伍分裂问题，概率最高的为模型预测的分类，结果可想而之，该模型预测狗类的概率最高，)

二、回归问题

回归问题预测的是值，模型的输出是一个实数值

三、目标函数

• 参数是逐步调整得到的，机器学习不能直接计算得到最终正确的值，只能调参
• 目标函数可以帮助衡量模型的好坏

3.1分类问题的目标函数

• 需要衡量目标类别与当前预测的差距

  三分类问题输出例子：[0.2, 0.7, 0.1]

  三分类真实类别：2 >one_hot->[0.0.1]

四、one-hot编码，把正整数变为向量表达

• 生成一个长度不小于正整数的向量，只有正整数的位置是1，其余位置都为0

五、分类问题目标函数的描述损失函数

• 平方差损失
  $$\frac{1}{n}\sum _{x,y}\frac{1}{2}(y-Model(x){)}^2$$

• 交叉熵损失
  $$\frac{1}{n}\sum _{x,y}y\ln (Model(x))$$

实战之分类模型的数据读取与展示

一、在tensorflow2.0的版本下使用jupyter

1、导包

import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf

from tensorflow import keras

print(tf.__version__)
print(sys.version_info)
for module in mpl, np, pd, sklearn, tf, keras:
    print(module.__name__, module.__version__)

2、下载数据

Fashion-MNIST 是⼀个10 类服饰分类数据集。Fashion-MNIST 中⼀共包括了10 个类别，分别为：t-shirt（T 恤）、trouser（裤⼦）、pullover（套衫）、dress（连⾐裙）、coat（外套）、sandal（凉鞋）、shirt（衬衫）、sneaker（运动鞋）、bag（包）和ankle boot（短靴）

fashion_mnist = keras.datasets.fashion_mnist
(x_train_all, y_train_all), (x_test, y_test) = fashion_mnist.load_data()
x_valid,x_train = x_train_all[:5000],x_train_all[5000:]
y_valid, y_train = y_train_all[:5000], y_train_all[5000:]
print(x_valid.shape, y_valid.shape)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

运行结果

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-G75YSYQK-1575541836686)(/Users/bobwang/Library/Application Support/typora-user-images/image-20191202181056249.png)]

3、展示数据

def show_single_image(img_arr):
    plt.imshow(img_arr, cmap="binary")
    plt.show()

show_single_image(x_train[0])

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-E18CHr5I-1575541836687)(data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAP8AAAD8CAYAAAC4nHJkAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAEjxJREFUeJzt3V1slPeVBvDn8BUIGPNhY1CAdWlCICJacCZkI1arhIgqXVUivWhULhArkboXjbSNuEjETXOzUbTatpuLVSV3Q0qkNm0lmg2Kom6jaKVsJYTikKg2mA2EGHCwsI0N2ITwefbCL5FD/J4zmXdm3tc9z0+KbM/x6/l74ofx+Pw/RFVBRPFMy3sARJQPhp8oKIafKCiGnygohp8oKIafKCiGnygohp8oKIafKKgZ9byzpqYmbW1treddEoXS29uLoaEhKedzM4VfRB4H8BKA6QD+U1VftD6/tbUVnZ2dWe6S6Ave1HSRsjLwV6VUKpX9uRX/2i8i0wH8B4BvA7gPwDYRua/Sr0dE9ZXlNf9GAMdV9YSqXgXwWwBbqzMsIqq1LOG/C8DpCR/3Jbd9iYi0i0iniHQODg5muDsiqqYs4Z/sBdVXXoSpaoeqllS11NzcnOHuiKiasoS/D8CKCR8vB3Am23CIqF6yhP89APeIyDdEZBaA7wPYX51hEVGtVdzqU9XrIvI0gP/GeKtvj6oertrIqGzd3d2ptX379pnXHjx40KzfuHHDrC9dutSsr127NrX26KOPmtc+9NBDZj1iK6+aMvX5VfUtAG9VaSxEVEec3ksUFMNPFBTDTxQUw08UFMNPFBTDTxRUXdfz0+SOHDli1nfu3GnWrWXS169fN6+dMcP+EZg2zX5+8Oqff/55xdeuXr3arO/atcusP/XUU2Y9Oj7zEwXF8BMFxfATBcXwEwXF8BMFxfATBSXeDqjVVCqVdKru3nvz5s3Umtey8rS0tJj1oaEhs97Y2Jha8/7/zpw506x7rcLp06ebdW9JsGVkZMSsL1++3KyfPn3arNdSXjsLl0oldHZ2lvXF+cxPFBTDTxQUw08UFMNPFBTDTxQUw08UFMNPFBSX9CasPj6QrZd//vx5s+71+WfPnm3W77zzztTamjVrzGu95cReP9obu9XnP3XqlHntggULzHpDQ4NZP3ToUGqtra3NvNZTy5+Xein+CImoJhh+oqAYfqKgGH6ioBh+oqAYfqKgGH6ioDL1+UWkF8AogBsArqtqqRqDqoVa9mUffvhhs37y5Emz7o3N67UPDg6m1qw5AOXc98cff2zWvV79vffem1prbW01r/XW4w8MDJj1LVu2pNa8/9/WY1rO9d4+Bt4+CPVQjUk+j6qqvdsEERUOf+0nCipr+BXAn0TkfRFpr8aAiKg+sv7av0lVz4jIEgBvi8hRVX134ick/yi0A8DKlSsz3h0RVUumZ35VPZO8HQDwOoCNk3xOh6qWVLXU3Nyc5e6IqIoqDr+IzBWRhlvvA/gWgO5qDYyIaivLr/0tAF5P2lAzAPxGVf9YlVERUc1VHH5VPQHgb6s4lprKuk/6s88+m1o7fvy4ea33tw5vb3xvPb91DLbXK1+3bp1Zv3Dhgln31txbY+vt7TWv9axatcqsW+cZnDhxwry2vd3++3VHR4dZL0If38NWH1FQDD9RUAw/UVAMP1FQDD9RUAw/UVBhtu7O2uo7cOBAas1rOXn37bX6vOOerXab13Ly7vuBBx4w696SX2vb8rVr15rXLlu2zKxfvnzZrF+6dCm1tmjRIvParq4us/7XgM/8REEx/ERBMfxEQTH8REEx/ERBMfxEQTH8REGF6fN7vK2Wh4eHU2tz5swxr50/f75Z97bXvnr1asX1O+64w7z2ypUrZj3rtuKlUvpu7vPmzTOv9Y4295blLl68OLU2Y4b9oz80ZG9I7W1ZPhW2rOMzP1FQDD9RUAw/UVAMP1FQDD9RUAw/UVAMP1FQ7PMnvGO0R0dHU2tev/ratWtm3es5e716a46Ct17f+9pLliwx694cBGtNvXfE9qxZs8z6woULzbr1uHjzG6wtxwF/HgD7/ERUWAw/UVAMP1FQDD9RUAw/UVAMP1FQDD9RUG6fX0T2APgOgAFVXZfctgjA7wC0AugF8KSqjtRumLXnrQ23fPbZZ2bd6nUD/jwBrxdv9fK9ve29vQjGxsbMuve9W3MYvD6+d+aAN7aLFy+m1ubOnWte6+3vcPjwYbPe1tZm1ougnGf+XwF4/LbbngPwjqreA+Cd5GMimkLc8KvquwBu38ZmK4C9yft7ATxR5XERUY1V+pq/RVX7ASB5a88BJaLCqfkf/ESkXUQ6RaRzcHCw1ndHRGWqNPxnRWQZACRvU1doqGqHqpZUtdTc3Fzh3RFRtVUa/v0AdiTv7wDwRnWGQ0T14oZfRF4DcADAvSLSJyI7AbwIYIuIHAOwJfmYiKYQt8+vqttSSo9VeSy58vq206al/zs5MmJPcfj000/N+v3332/WvX631cv31tt7+/I3NDSYdW+/AGtsXi/dm9/grbk/e/Zsaq2pqcm81nvMDxw4YNa3b99u1ouAM/yIgmL4iYJi+ImCYviJgmL4iYJi+ImC4tbdib6+PrNutcS8tpCqmnWvpeUtCba2BvfG5rXqvC2urRYoAMycOdOsW7yxea0+63HzWpjeselHjx4161MBn/mJgmL4iYJi+ImCYviJgmL4iYJi+ImCYviJgmKfP9HT02PWrV69iGS6b68X7y19tXrpXi88K29JsDUHwTua3Pu+veutLdG9uRXetuLd3d1mfSrgMz9RUAw/UVAMP1FQDD9RUAw/UVAMP1FQDD9RUOzzJ7q6usy61Yu3etnl8I659tbMZ5mD4PXKvb0Issxx8OYIePXZs2ebdWvbcu9re7yj5z766COzvnr16kz3Xw185icKiuEnCorhJwqK4ScKiuEnCorhJwqK4ScKyu3zi8geAN8BMKCq65LbngfwAwC3mp27VfWtWg2yHvr7+836okWLUmvemvkFCxaYda/n7K0tt/rZXi/cm6Pg7dvvseYJeOv1vfv25hhYe+9737d3ZoDHO/J9qvT5fwXg8Ulu/7mqrk/+m9LBJ4rIDb+qvgtguA5jIaI6yvKa/2kR+YuI7BGRhVUbERHVRaXh/wWAbwJYD6AfwE/TPlFE2kWkU0Q6vfnQRFQ/FYVfVc+q6g1VvQnglwA2Gp/boaolVS01NzdXOk4iqrKKwi8iyyZ8+F0AU38rU6Jgymn1vQbgEQBNItIH4CcAHhGR9QAUQC+AH9ZwjERUA274VXXbJDe/XIOx5MpbM2/1hb1+tLdHvNeL9/b1t/rd3np8r59tnQng3bf39b29BLJ83959X7p0ybzWm1vhaWxszHR9PXCGH1FQDD9RUAw/UVAMP1FQDD9RUAw/UVDcujvhtY2s1s/58+fNa72ZjV7La2xszKzPmTMntXb58mXzWu/7njt3rlnPMmU7y5JcABgZGTHrd999d2rt6NGj5rVe63fhQns5i7d19+bNm816PfCZnygohp8oKIafKCiGnygohp8oKIafKCiGnyioMH1+7xhsb/novHnzUmvnzp0zr21qajLrHq/nXKtrAX9bcm/JsLUk2Nu621sK7dUffPDB1Nonn3xiXustyfXmZhw7dsysFwGf+YmCYviJgmL4iYJi+ImCYviJgmL4iYJi+ImCCtPn97Zq9urWNtDemvclS5aY9TNnzph163hwALhw4YJZt3hr6rNebz1u3hwEb0vzvr4+s27NQZg/f7557cmTJ826d6y6d+R7EfCZnygohp8oKIafKCiGnygohp8oKIafKCiGnygot88vIisAvApgKYCbADpU9SURWQTgdwBaAfQCeFJV7Y3Uc+TtrW/tfQ/Ya8+9nu+qVavM+sWLF8261w+36t7YPN6aeY/1uHn78nt9/oaGBrNu/T/17tub9+HNE7D2fyiKcp75rwPYpaprAfwdgB+JyH0AngPwjqreA+Cd5GMimiLc8Ktqv6oeSt4fBdAD4C4AWwHsTT5tL4AnajVIIqq+r/WaX0RaAWwAcBBAi6r2A+P/QACw57ASUaGUHX4RmQdgH4Afq6r9IvXL17WLSKeIdGY5142Iqqus8IvITIwH/9eq+ofk5rMisiypLwMwMNm1qtqhqiVVLXkHVhJR/bjhl/FlWy8D6FHVn00o7QewI3l/B4A3qj88IqqVcpb0bgKwHUCXiHyY3LYbwIsAfi8iOwGcAvC92gyxOryXHF5Ly1oe6rXqvO2vre2tAeDatWtmPQtryS3gb2nuPW7WluleC9Pbbj3L0ebetuEerzXsPW5F4IZfVf8MIG3R9mPVHQ4R1Qtn+BEFxfATBcXwEwXF8BMFxfATBcXwEwUVZutur2c8a9Yss25tUe0t31y8eLFZP3LkiFnPMgfBO0Lb+7493tbd1hyGrHMMssx/WLNmjVl/8803zbo3W9X73oqAz/xEQTH8REEx/ERBMfxEQTH8REEx/ERBMfxEQYXp84+Ojpp1b5toq5/d2tpa8bUAcO7cObPubf1t7Rfg7SXgzSEYHh4260NDQ2bd2uLa6+NnmXsB2Mdkb9++3bzW6/N7ezB4P09FwGd+oqAYfqKgGH6ioBh+oqAYfqKgGH6ioBh+oqDC9Pm9I5cbGxvNurXv/+bNm81rly5data9o6a9Y7avXLmSWvP60R7v+gULFph1az8Bbz2+V/eO2bbmATz2WLZd5719/72ftyLgMz9RUAw/UVAMP1FQDD9RUAw/UVAMP1FQDD9RUG6fX0RWAHgVwFIANwF0qOpLIvI8gB8AuNUA362qb9VqoFl5/WrvrHerX71hwwbz2oMHD5r1Dz74wKx7e8xfvnw5teateffmGGTtxVvnJUybZj/3XL16teKvDQBjY2OptZaWFvNab19+b+7FVOjzlzPJ5zqAXap6SEQaALwvIm8ntZ+r6r/VbnhEVCtu+FW1H0B/8v6oiPQAuKvWAyOi2vpar/lFpBXABgC3fo99WkT+IiJ7RGRhyjXtItIpIp3WFFkiqq+ywy8i8wDsA/BjVb0I4BcAvglgPcZ/M/jpZNepaoeqllS15L2OIqL6KSv8IjIT48H/tar+AQBU9ayq3lDVmwB+CWBj7YZJRNXmhl/G/1z8MoAeVf3ZhNuXTfi07wLorv7wiKhWyvlr/yYA2wF0iciHyW27AWwTkfUAFEAvgB/WZIRV4rWkvC2uLceOHTPrr7zyillfuXKlWR8ZGTHrVlvJ+768Lc29VqG3rbjVErNacYC/XNhr327atMmsW7w2o9VeBYCenp6K77teyvlr/58BTPYTUNiePhH5OMOPKCiGnygohp8oKIafKCiGnygohp8oqDBbd69fv96st7W1mfXDhw+n1rzlwF4/+oUXXjDrVH/PPPOMWfeWI3vLvIuAz/xEQTH8REEx/ERBMfxEQTH8REEx/ERBMfxEQYm1JXXV70xkEMDJCTc1ARiq2wC+nqKOrajjAji2SlVzbH+jqmXtl1fX8H/lzkU6VbWU2wAMRR1bUccFcGyVymts/LWfKCiGnyiovMPfkfP9W4o6tqKOC+DYKpXL2HJ9zU9E+cn7mZ+IcpJL+EXkcRH5PxE5LiLP5TGGNCLSKyJdIvKhiHTmPJY9IjIgIt0TblskIm+LyLHk7aTHpOU0tudF5NPksftQRP4xp7GtEJH/EZEeETksIv+c3J7rY2eMK5fHre6/9ovIdAAfAdgCoA/AewC2qeqRug4khYj0Aiipau49YRH5BwBjAF5V1XXJbf8KYFhVX0z+4Vyoqs8WZGzPAxjL++Tm5ECZZRNPlgbwBIB/Qo6PnTGuJ5HD45bHM/9GAMdV9YSqXgXwWwBbcxhH4anquwCGb7t5K4C9yft7Mf7DU3cpYysEVe1X1UPJ+6MAbp0snetjZ4wrF3mE/y4Apyd83IdiHfmtAP4kIu+LSHveg5lES3Js+q3j05fkPJ7buSc319NtJ0sX5rGr5MTrassj/JOd/lOklsMmVW0D8G0AP0p+vaXylHVyc71McrJ0IVR64nW15RH+PgArJny8HMCZHMYxKVU9k7wdAPA6inf68Nlbh6QmbwdyHs8XinRy82QnS6MAj12RTrzOI/zvAbhHRL4hIrMAfB/A/hzG8RUiMjf5QwxEZC6Ab6F4pw/vB7AjeX8HgDdyHMuXFOXk5rSTpZHzY1e0E69zmeSTtDL+HcB0AHtU9V/qPohJiMgqjD/bA+M7G/8mz7GJyGsAHsH4qq+zAH4C4L8A/B7ASgCnAHxPVev+h7eUsT2C8V9dvzi5+dZr7DqP7e8B/C+ALgC3jgnejfHX17k9dsa4tiGHx40z/IiC4gw/oqAYfqKgGH6ioBh+oqAYfqKgGH6ioBh+oqAYfqKg/h9nkfle/x5XuAAAAABJRU5ErkJggg==)]

多个数据展示

def show_imgs(n_rows, n_cols, x_data, y_data, class_names):
    assert len(x_data) == len(y_data)
    assert n_rows *n_cols < len(x_data)
    plt.figure(figsize=(n_cols*1.4, n_rows *1.6))
    for row in range(n_rows):
        for col in range(n_cols):
            index = n_cols * row + col
            plt.subplot(n_rows, n_cols, index+1)
            plt.imshow(x_data[index], cmap="binary", interpolation= "nearest")
            plt.axis("off")
            plt.title(class_names[y_data[index]])
    plt.show()

class_names = ["T-shirt", "Trouser", 'Pillover', "Dress",
                "Coat", "Sandal", "Shirt", "Sneaker", "Bag", "Ankle boot"]
show_imgs(3, 5, x_train, y_train, class_names)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-aDnOHgge-1575541836688)(data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAagAAAEqCAYAAABAysQTAAAABHNCSVQICAgIfAhkiAAAAAlwSFlzAAALEgAACxIB0t1+/AAAADl0RVh0U29mdHdhcmUAbWF0cGxvdGxpYiB2ZXJzaW9uIDMuMC4zLCBodHRwOi8vbWF0cGxvdGxpYi5vcmcvnQurowAAIABJREFUeJzsnXe4JUW1t99FkJyTDDnnLNEhKHAJMgRRUJKgoARF1IdwvVyCcsHPi8BFFJSsCAhIFhBBBxiiBMkZZghDjkMShPr+6P51r71PnT3nzJzQe1jv88wz+1T17t1dXd291q9WrbKUEkEQBEHQNKYa7gMIgiAIghzxggqCIAgaSbyggiAIgkYSL6ggCIKgkcQLKgiCIGgk8YIKgiAIGkm8oIJ+Y2ZjzGz3XuoWN7N3hviQphjMbKyZbTLcxzFUmFkysyX7WzeRfe5uZmMm/+i6gym5DaeIF5SZ7WRmd5rZO2b2gpldbWYjJ3Ofo81sz4E6xuGmbBv9+8TM3nd/7zxQv5NSeiqlNPNEjqXXF1yTMLORZnaLmb1lZq+b2c1mtuZwH1cTKe+XN8xsuuE+lsHCzDYys+cGcf/Rhm10/QvKzH4InAAcDcwHLAz8GthmOI+raaSUZtY/4BlglCv7w1Acg5lNZWZd0efMbFbgSuCXwJzAAsCRwL+G87j6iplNM4S/tSiwPpCArYfqd6ckog3zdMXDojfMbDbgJ8B+KaWLU0rvppQ+SildkVI60MymM7MTzGx8+e8EWSdmNoeZXWlmr5RWy5VmtmBZ9z8UneWk0sM4afjOcngwsxnN7Fwze83M3jSzO8xsbrfJYqV3McHMrjGzOcvvLWlmye1njJn91MxuBd4FzgPWBU4p2/aEIT2xvrM0QErpvJTSxyml91NK16aU7pP8YWbHln3naTPbQl80s9nM7PTSm3/ezI4ys6nLuiXM7G9lu75qZn8ws9lzB2Bmy5b7/lr59wgz+1PZZ582s/3dtkeY2UVmdo6ZvQ3sPpiN08ZuwG3AWcA3fIWZnWVmvzKzP5d95XYzWyK3k9JjfdbMvpCpm65s72fM7CUzO8XMZuhwTGZmvyy930fMbGNXMcLMLi+94ifMbK+23+nxzDCzmYCrgRFOeRjRr1bqTLRhjpRS1/4DNgf+DUzTS/1Pyos+LzAPcAvw07JuLmB7YEZgFuBC4FL33dHAnsN9joPUbmOBTSayzX7ApcAMwNTA54CZy7oxwOPAUmX73QQcVdYtWXSraj9jyt9bDpgWmKYs232422Ei5z8r8BpwNrAFMIer2x34CNirbJt9gPGAlfWXAr8BZir73h3Ad1z7bApMV/bJG4ET2q8NsDqFp7tVWT4VcBdwGPAZYHHgKWCzsv6I8pi2LbedYQjb6glgX2CN8hjmc3VnAa8Da5XX/g/A+a4+lW2yGfAssFZ7Xfn5BOByCm92FuAK4Jhejmd3iufCD8o+tyPwFjBnWX8DhcoyPbAq8AqwcVnX6ZmxEfBctOHQteGwPwgm86LuDLzYof5JYEv392bA2F62XRV4w/09mk/3C+rbFC+SlTJ1Y4BD3N/7A1eWn3MvqMMy3999uNuhD+20XPlweK68WS+nkJF3B55w281YPgg+W9b/C/eCAL4O/L2X39gWuKft2hxZ/uYXXPnawDNt3/1P4Mzy8xHAjcPQRiMpHqhzl38/AvzA1Z8FnOb+3hJ4xP2dyvMY197XqB+8RuF9L+Hq1gWe7uWYdscZDGXZHcCuwELAx8Asru4Y4Kzyc6/PDAbpBRVt2Pu/IdOpB4nXgLnNbJqU0r8z9SMoLpoYV5ZhZjMCx1N4YXOU9bOY2dQppY8H8ZgbRyk/veWKlqa4KUYAF1gxHvN74FDXzi+67d8DOgVGPDtwRzt0pJQeppTKzGxZ4BwKK/QvuPNPKb1nZlC0wZwUFucLZRkUHs2z5X7mBU6kkJBnKeveaPvpvYEbUkp/d2WLUEgjb7qyqSm8VzEc7fwN4NqU0qvl3+eWZce7bSbWVw4AfpdSur+X35iHwgi4y7WpUZx/bzyfyidiie79EcDrKaUJbXWfKz/3+swYRKINe6Grx6CAW4EPKKzQHOMpbmyxcFkG8CNgGWDtlNKswAZlua7epybNeyrGWGZ2/8anlD5MKR2RUlqOwsLbjsJjnaSfmMjfjSel9AjFS3vFiWz6LIUHNXdKafby36wppRXK+mMozn/lst/tQt3nxN7AwmbmH1DPUli7s7t/s6SUtvSHOWlnN2mU4xc7ABua2Ytm9iKFJLSKma3Sj119FdjWzA7opf5V4H1gBXfus6XO0aILmHsSU9/744E5zWyWtrrny8+dnhkD3r7Rhp3p6hdUSuktCk3+V2a2rRUD+9Oa2RZm9nOKAflDzWweKwb4D6OwgqGwXt8H3rRigP/wtt2/RKHzfyoxsy+a2YpWRN29TSFBDJRn2fi2LQMUfmR14MxCFFLdbZ2+l1J6AbgW+IWZzWpF5OISZrZhuckswDsU/W4B4MDMbiZQePYbmNnPyrI7gLfN7GAzm8HMpi6vz3CGvW9L0SeWp5DIV6WQRW+iGPTvK+OBjYH9zWzf9sqU0ifAqcDxpQeKmS1gZpt12Oe85f6mNbOvlsd1VUrpWYoxkWPMbHozWxn4FsW4DnR+ZrwEzGVFcNZAEW3Yga5+QQGklI4DfggcSjFQ9yzwXYqB6qOAO4H7gPuBu8syKKSaGSgsi9uAa9p2/X/AV6yI0jpxkE+jiYwALqZ4OT0IXEfR8QaCE4CvWxEdeNwA7XOgmUAx7nO7mb1L0UceoPC8J8ZuFIEMD1HIdxcB85d1R1IEQLwF/JmijXuQUnqTIphiCzP7aSk7j6J4gD1N0W9PAwbyYdlfvkExBvZMSulF/QNOAna2foS6p5SeoXjAHmz5+YcHUwQS3GZFlOJ1FApIb9xOEcTzKvA/wFdSSq+VdV8HFqV4qF8CHJ5S+mtZ1+szo/SizwOeKvvuQEh/0YYdUNRREARBEDSKrveggiAIgimTeEEFQRAEjSReUEEQBEEjiRdUEARB0EiGeqJuV0Zk+ECS1mkBk82k7Gyy2/CBBx4A4N13363KHn74YQBOPvnkquzcc88FYIklsmm/emXMmDpL/1FHFUGTP/3pT6uyqacu5gYutthiAMwxxxxMBv1tw67sg4PIsPTBKYxow8kn24bhQQVBEASNpNtTHfWKvIQ//elPVdntt98OwMcfF/NNP/vZz1Z1yy23HABf+EKdBHjttdcGBtxrGjbOOaeYK/fOO8V6gvPMM09V97nPFVlK5p133qps1VVXBWDBBResytZbbz0AZpihSII8evToqu6JJ54A4F//qlek2GyzYh7gLLPUk87vu+8+AG6++WYAFlmknnS+9dax0kAQBAXhQQVBEASNJF5QQRAEQSMZ6kwSg/JjDz30EADf+ta3qrI777wTgH//u05yPs00haI51VRTtfwP8MEHH/QoW3rppQH40Y/q7DZ77jmgq8AP+uDqlVdeWX3+29/+BsAuu+wCwPjx46u62Wcv1sxbZpk688kVV1wBwHHH1dmIFFix5JJLAnD//XXy5LnnLtYzPOigg6qynXbaCYB//OMfVZnaesYZZwTg/PPPr+o233xzoJYG+0AESUweMcA/+UQbTj4RJBEEQRB0D13jQX3yySdAq4cj5ptvPgBeffXVqmy22Yocmv78pp12WqD2qhTuDHXghOeNN4plenyQwLPPTnzJnX6EpQ+65XXSSfVq9c8/X2TDX3755QFYeOGFe2w//fTTV5913mp7gL/+tcgH+fbbbwOw1lprVXUKuphzzjmrsqeeegqAjz76qCrT/p577rmWbaD2qg44oLdVA3oQHtTkEdb/5BNtOPmEBxUEQRB0D/GCCoIgCBpJo+dBeWmpXdp788165WtJfF6eklS07LLLVmUKppDspu9BLfE988wzVZkCB/wcnrvvvhuA1VdfvdfjzcmQw8W9995bfVYAxIQJxUrNClaAel7TZz7zmapM85pmnXXWqmyjjTYCannUB6G89VaxarwPvvDXREjue+WVV3ps89hjj/XtxIJPFTnZXP3N13344YdAqxSvMi8zTzfddEB9j/v5f3oWKOjHoz4LtWSu+YLBwNOcJ2kQBEEQOBrpQXXyRNZdd10Axo0b12N7H5AgS0eelN/uySefBFq9JXkXiy66aFUmK+zll1+uyjbddNOWY/MWlcp8wIUPxBgOvHei89C5vvDCC1Wd8uLJu4K67WaeeeaqTPVqS2955s5VWSV8dglZvtree1za7yDmP2wEOr+JnVtuO3kCaivv9U6JbQX589pjjz0AePrpp3vUKVsK1O314osvVmXynLRfn1VF6ozPcKJMK1tttVVV9oc/FCucn3HGGf05lUEl118GS9npax+eHMKDCoIgCBpJvKCCIAiCRtJIiS/nMh588MFAPXDv5/BooN7LWQoA8IOlK664IlBLTHLz/fZjx47t8duLL7549VnzqzR359vf/nZV99vf/hYYflkP6kwaXiqTfPn6668DreelNlEbeXJBDxp4fvDBB6s6BZP44BPJJe+9915VJulQZQsttFBVJ2lGCWUBVllllV7Ps1vJ9XEFiCiDCcAvfvELoDVQxfe5Tws+wEHzGZXMWcFPUAf76H+o78eVVlqpKpMML8naLz2jjDN+CEBSvu/HBx544CSfz2CR61c5ie/GG28E6qwvSy21VFWntvHDHco+ozmUud/ysqquiX+eKjn3Bhts0MezCQ8qCIIgaChd40HdeuutQG31+23kQXlvQd6R92a03RprrAHUwRJQW/padgNg/vnnB+D999+vymRpKVuCz0XXJJRHzy8pIstTlrq8Jqg90lxYuLxGqK0wDSr7wWUFXWhZE6i9H3ltUHufCnTxnpza/Oqrr+6xjymdyy+/HGjNiKL2fvTRR6uyX//610Dd9t763XLLLYE6mAhgrrnmGqQjHjpyGW+0kKbvs/rsp1DoWeGDl2TtK3hHXhPU6oDuF4CXXnoJaG1L/6xoCn0NXND56PngPU4pJn4pHWWQ8feqcmieeOKJAJxyyilVnfqm93yVv9P3Td/GOcKDCoIgCBpJIz0o4S0eWeB603tNXmMasnz8Z03Ig9payoWlK4zUh1TLq/K54mRByeLy1q4061yOu6FmzTXXBFqziEsXvvDCCwH4j//4j6pOHuFrr71Wla222mpAqxcqy1QWqLdslbvPW2O33XYb0BruLw/u4osvBuCb3/xmVTfTTDMBrTn+pmR8e+v6nHnmmVXZ/vvvD7T2Y3m+slJ9H5QXpvFQqD3QL3/5y1WZrm03I4vc38cKufdjRXqO+D6o7TS25Cecy2v1yon69tFHHz1wJzAI5Dyn3Ji48mBq+9w0BuUiBdhwww0BuOyyy6oyJSvQc9KPJet54se95C1NzGvyhAcVBEEQNJJ4QQVBEASNpNESn88WoXBQSXB+8E1ym5dB5NZ71131yn7gJUEFP/isEZIB5phjjh77lVzoB2MltTRB4tOMdz/zXS77VVddBbQGM3zxi18EWqWRO+64A2gNz1U7SS7xMoA++zaX3OdDz/W7CmQ59NBDqzrf1t1Ef2fVqx95SVnXwEvbyvrxs5/9rCqTvK2wfp8zToEDfuFJBQMdccQRVZmXarqBTssC+SAJSUoTuw6SpbR9LnOJfz743J/dRq5vKjhCcpsPmNJzV6HlAKNGjQLqYAmo73NNi/AZTXIynpdM+0p4UEEQBEEjabQH5YMThCx8P7FOVqj3oPR2929tWfMa4PfegrwwbwVocNFPQNNCfRrM99auJq3mMp03AXknCuH+7ne/W9UpcMR7Og8//DBQB5D4fahuxIgRVZ0GRq+//vqqTFb+448/XpUpPPeoo45q2We34a1utZ8fkO7kVcmL/eMf/1iVKaDFh+uOGTMGqPub/yyPXQPYUHul6qdQ3x/eq+o2fBi4yHlVUjb84PwCCywAtKodCrNWe3mvX88A/5t+Un+3ket/UkCUx9BPylVf9lMbFF7uc3Xq3tb0Er/6hFQq791OSlh+eFBBEARBI4kXVBAEQdBIGi3x+Txvctk1EK/FwqAexPfyiqQ9P9ApF1SuqXfrtb2X7CQZ5qQBDUz731S2i1133bXP5zjY5AZ/dcxewpAk5F1ySR2aywSw0047AbU86mVYBa6ssMIKVZkkF7+d2jiXtUJ1Tchn2Bs56S53vDlpRf1X87z8oLOkOx/MoDKfzcPn6oPWtlXf9sEX2ofP5tGkOXt9IdeW6ltegldWDd+3tZ1fGkdyv+5tv71+y8/n87/RbeTaTvM51W9zQWfXXHNNVfbnP/+5pQ7qvqa28c9T/aYfRsktADkxwoMKgiAIGkmjPSjNdoaeg9DeM5Cn4wMnZBHkcvHlBlJzYZHa3ntQ+g1ZD352+iOPPNLHMxteFAjhrXK1r89KoJyF//znP6uyX/7yl0A94P7AAw9UdbLQ/Yzy3CKO8sw0eO0Z6EXVJpW+hI17q1OWom9TeaU+8EbZM/7yl78Adfgu1N6pXwDvlltuAVoH6dXn5Kn6a6Z29kESura/+93vqrKdd94ZmDQPaiAXqvNWdy4QQm2cuz9/85vfAHVwDtTh0/7ZoX7pnw9qJ38N24/JH48+57KqDyb9betclpxO322fNgL1uX7ta1+rytSHb7rppqpMfV7THvyzVjk1/fPB5wXtK814GgRBEARBG/GCCoIgCBpJoyU+zbWBzq6uXEsvI8n99vJcOz5uX667d+u1P1/WPufKyzfenW0yCk7wspHK/ECy5jz4TBJCASxbbLFFVaZBZS8D6Lr5ZQokg+UknaYgGdgHcrT3QS/3qJ/5eXdaNNL3C8090/79wozXXXcdUC8mB7D++uu3/CbUcoz+9/PU1Kd9QISyIGy66aZVWVOCIzrJepCX0c4991wALr30UgC22Wabqk4yuz9/ycZePtZ1VQCJv276Td/m2p9fxFBZO4Yb/9xTH53YvaVMIrov/cKuCizzS+noeedlPCU6Vp/zx6G5jf75OCmEBxUEQRA0kuaasLQuBpgLhxQarPMWUs7jklXRyRvzXpU+eyta1oXfTsj70HIS0DMkeKjpNEDqwz5zqfBffPFFoLb2oR78VFv7qQBqG7+92tzv11tm/TneoSQXAt++8J0f4Nf0A+8tbb/99gCcdNJJVZmWbdCsei0OB3DXXXcBsOqqq1ZlskR9m6mfKUTdZ1DRDP7FFlusKtM18IPU7QvW9YfcNcpldcjdZypr/x/qPpXzmvwSJIcffjhQe+8+40F7rkyoPU1/vXLBBO11/ji0X9/fh8KDyh1f+1SM3BQH/5xU1hKFikOd/UHn6DPIaArPeeedV5UpKMz3V/VJeaF+So+CdPwz+YILLgBgjz326HmivRAeVBAEQdBIGu1B6S0PdSiptH4/fiKLx+udept7S1hWhbeuhCw5r6Nqu5z+r315q0x4K2u4PahO+Pxuald//rKavJUrCyrntaqdcrqzb3MfFtwEZO350GR5GPofamtTExP90tWyUn3W8ZEjRwLwn//5n1WZxpmUb8/vX4sIrrzyylWZ2tm3qcJ6Vef7oKxpn/tQ23uvX1ayFjOcFHxf6etE5b54yF6BOP3004F6IUaocw+OHTsWyE+i9b+j4/Tjq+1jNblJ1+r/vuyee+6pyrbeeuuJnsvkomvm77P2tvb58S655BKgzrcJ9fiaX+RVHrba5Iknnqjq5MH7DOdaTNOPJUuBUft7T17PXT/ZWZPUJ9ZvPOFBBUEQBI0kXlBBEARBI2m0xOfd2nZ5LudOendRLruXpySF5MJIc7PHtb/cdpqBnZOzfDaBJpPLO5gLs/fSkGQPXY9cMIHPYqD9+mvpf3e40DIDUC+g6AMRFAziAxYkG//9738HWgfnlXXj7LPPrsoUHOF/SyHfmq6Qk4B9RhIdk5dWFAihe8FLprmMICrzUtCkLB4nBiJfovqPD7PXILrP+KD28UuKKHBE0pI/f4WD5xYY9EEPum91b+dC0HPnl1sCaKDIBZXkMqtIllNWkhtuuKGq0/PJP5d8lgihACj9ps/+ouk9/jn2hS98AWgNXNM+crlNc9M01Cf98WqRzt4IDyoIgiBoJI32oLwlIYtAlpG3dmX1+8FSDc55S1H7U3CAHzTN/WZuWfMll1wSqK1cb+HIsvODvBOzEIYTb1HmPE7hPR55ESrz2Ypz3qSsYR+Q0YmBzPOWQ33EW5Ua7PYehvqUt8S1eKC28wPA8sJ8H9TAs+8/agf1G+/pyNr0k8v1+/LooGdGfb8PTST1x6b9ec92cjwoeRY+wOOYY44B4O677+6xvV/UUuet3/f9QhOON9lkk6pMbegnf7eHjcuSh3pg39+XupY+lFoenPqbv/Yqy3ke/loONLk+r2AXeUtQByyor/mAMZ23D/lWO+X6t/qGD2LS4oXeW9SkcykFULeF2tx7UDo2f056Zo8ePboqCw8qCIIg6EriBRUEQRA0kkZKfJKN/CClBpWV/ym3+FVuQDFXJrfWy1mSu3KBAz4gY8011wTqgW8/kCi32c9BGW5yCxbq/P1sc7W1D4jILZUhtJ1363MZAHLLJei7knm8HDXYmSR0HF6a1DHmzt2f34orrgjUkpq/zmpn398+//nPA62ykOYfSfr02+cWwdRnL8lJKtHxeolL+/PBLpKA/DyY3FIn/eXnP/959Vn35/7771+VSe7z8xl1DJLPFPAB9flLSoVaZvL9R3PJJEt5OUv9x8t5kra8dKrrqvs3l7Mz1x8GM3+kruNpp51WlWm4wP+upHQ9l3zfyC0zpDIvP6s91YY+MEVtKKkP6mvo5bn11luvZXuf/1DSrZf9dRySw/tCeFBBEARBI2mkB6W3uX+ry+LRm9lbXspu4MNN/Sxo0W6d58LHc+GmPsOALGVZguPGjavqZHF5i7GJ6Ji9B9Ueugv5pdlzC0aKnPej7/p2bc/j57NxDzYKEffehDI3eAtQfcoPQGuwX5nAlWkcaiveW7PeMxRqt1x/U//JZTrx6DcUQOEzyuu8chlOvBIwOQtDapDe93MpCj70XoEduYwM6m/eM5A64sPsFYjhPQK1q54Puf7pvSp5rbnAkNy9Km/QXwfdK7nnyuSgcwb4yU9+ArReG+Vu9NdT38kFh+Wmy+Roz+rg72e1oVcZ5HF75Ur9QKqSV1oUgOb7nLw23+bqw/4+84QHFQRBEDSSeEEFQRAEjaSREp/cPi+RtGc1WHzxxau6XGp3fc4ti+Hdzvb9+7kPkg68RKFj0nZehpS8Iomgqfj5MGJiS4+I9sFkLz3ocy5BpN9O7ao5LkMp8WmZiyOPPLIqW3755YHWgXUtpeD7Q/tChX4ekPqBl5klxfj+pjaVfJKTQHy7azvfpjomBUvkZEKP6v21k3zVaemT3vjb3/4G1IPkULehX45Bi+D5eVrtGVj8+UuC89JSLiGu2jh3rhoC8NtLPlp22WWrMsm12pckR78PP0dLgRY+WCMX5NNXdC20dAi0Lhoo9Fzyz5l2ed3XqU28xJdLBN2+LImvU9vlMmn4NlebSJL1S7fklqRRG/vrq0Cbo48+usdvQXhQQRAEQUNppAeVG2CT1SDr31uDsmpyixl62i0Dv//c8hEq89aIBiRzodeypCYnR9lAk/OMZPl770Dnk8sG4c+/L23tz7/ToK23/IaKRRZZBIAzzjijKlPQiM9WIIvOe8PypPX/OuusU9XJe/aZJ+Qp+msgq1vhzd5qVtv7dlG7+b6qQX9dCz/AnAuw0LX1QQLbbrttj+36yr777gvALbfcUpUpHNofy0orrdTjd3X/6H9vTStIxWc8EN5zUbvqt3zb6Hr53IWy3HOh12ob/5vtC1P63/LZFRQwMSke1FFHHQW09hddd18mj8UH8LTnCvRto7bItVcuWCWXEUbPQH+P6xw7hbv7KTfyPr2ioHp/bOojvREeVBAEQdBIGulB5RZpk1WTs5AU7pjzuLxe2+4deMtWb/Xc4m85b0F69pVXXlmVSc/Phfg2CVmLvj1yYceyrnzIrr6jtplYuLKsN9+GfQ2nHirkVel/gF122aXHdtLab775ZqDV0lUOPHk3kPd+ZAn/4Ac/APKTm/14iCxQ75koPF8WsR9T1P79+Iksc29BT07GfV1zLcjoP/trqvEoH1ascUcds99e7e/HOdTf/H2sz7LqfXutsMIKQKtlftZZZwFw3HHHVWV6fmhf/jrkVjFQmPXLL79cleXGsvuKcnr6aSoa9/TXLpcjU/eUvy/bj8m3q7bz92D7go05j8tfh9zCie1jcP439dlf+1x/kEfq+5InPKggCIKgkcQLKgiCIGgkjZT4JEH5GeLt+aG8+61wXh96riAKH0wh91cyiA9/1SC3H0htX9QMavd01113BVolPrnJuUX8moRcfR8kIVffywZy571bL/kytyxGbrkIffbtKnnJD/x2A5J1fbjycCB5cLjIhXerH3jZa7HFFmv5H1pD09tR4ISXs3J5EnN5ODvxpS99CWiVAiXZSYry+9e94Pt2LijK76+/7LDDDkDrUIWmZHj5VfkM/b2qZ5CkNb8PZb3xcrXO0e9X8rT+93n3JGErY4rfh19OZfXVVwfqRSd9mLmenX4qhoZnckvd9EZ4UEEQBEEjaaQHpUFd/8ZX6LkWuPJvaw3+eitIb/zcIHQuPFdWmx9IzHkasqo23njjHvvNTaprMt4zUnvlFnrLWczCB4RoO+8tyavyA6hqz1xIe9B8JiePXycGa4K78nZOTmj9QKN7YNSoUR2322abbYbicFrYZ599hvw3eyM8qCAIgqCRxAsqCIIgaCSNlPgkwflZy5LgVlttNaB10at77rkHaB28Voy+H+iUFCjpzst5uUwSChjws6w1kKu8bT6XmSSupkt8uXlmuWU01P5+gLhd3skteui3V/BJboHAXE5AkVtoMQiCTxfhQQVBEASNpJEelCzs3DLMWmb7zDPPrMoUDumX1pYX4/eh8HVZ5D4sXd6PX/xLQRQ+0ELLeAsfli2v7eGHH+50esOOli5XeCj0zDINtUeU82TlEXkPSgERuUXd/MJsCovVbPogCIIc4UEFQRAEjSReUEHnZSxJAAAgAElEQVQQBEEjaaTEt+qqqwL1TGWoE2Tmkhv2ttjVUOBn9SuAQIEcTUWJGX2CxieffBJoTeSoTA+5BeQUcOIDIjTD30t3mu/hZ/8rKWYnIjAiCILwoIIgCIJGYu3LBwdBEARBEwgPKgiCIGgk8YIKgiAIGkm8oIIgCIJGEi+oIAiCoJHECyoIgiBoJPGCCoIgCBpJvKCCIAiCRhIvqCAIgqCRdOULysySmWVTYXeqm8g+dzezMZN/dEEQBMFAMKwvKDMbbWZvmNl0w3kcg4mZbWRmzw33cUwMM9vJzO40s3fM7AUzu9rMRk78mx33OdrM9hyoY2w60Yb9w8zGmtn7ZjbBzN40s1vMbG8z60rDuQlMaX1w2DqCmS0KrA8kYOvhOo4AzOyHwAnA0cB8wMLAr4FthvO4uolow0lmVEppFmAR4GfAwcDpuQ3NbOqhPLBuY4rsgymlYfkHHAbcDBwHXNlWdxbwK+DPwATgdmAJV5+AJcvPI4FngS9k6qYDjgWeAV4CTgFm6OV4di+P55fAW8AjwMaufgRwOfA68ASwl6ubjqJjjC//nVCWzQS8D3wCvFP+GzFcbd7Lec9WHtdXe6nPnltZNwdwJfAK8Eb5ecGy7n+Aj4EPyv2fNNznGm3YrH/AWGCTtrK1yvtlxfI5cDJwFfAusEmnexqYu2y/N8v79CZgqrLuYOD58nnyqL+3p4R/U2ofHM4GfQLYF1gD+AiYz9WdVXawtSiWBPkDcL6rT8CSwGYUL6e12uvKzydQvFTmBGYBrgCO6eV4dgf+DfwAmBbYkeJFNWdZfwOFNTI9sGp5MTcu634C3AbMC8wD3AL8tKzbCHhuuDtwh+uweXne0/RS3+nc5gK2B2Ys2/dC4FL33dHAnsN9jtGGzfxH5gVVlj8D7FM+B94CPk+h9kzf6Z4GjqF4YU1b/lsfMGCZ8jkxotxuUZzBOyX8m1L74HA15kiKl9Lc5d+PAD9w9WcBp7m/twQecX8n4D+BccBKbfvWy8sorC7vea0LPN3LMe1OYVmYK7sD2BVYiMKKmMXVHQOcVX5+EtjS1W0GjC0/b0SzX1A7Ay92qO/13DLbrgq84f6eYh+u0YYD0m5jyb+gbgP+q3wO/M6Vd7yny4fwZZQGqttmSeBlCg9s2uE+70FqyymyDw7XGNQ3gGtTSq+Wf59blnledJ/fA2Zuqz8AuCCldH8vvzEPhUVwVzkA+yZwTVneG8+n8oqUjKOQ9kYAr6eUJrTVLVB+HlH+3f69buA1YG4z623xyl7PzcxmNLPfmNk4M3sbuBGY/VM4VhBtOLAsQKGgQOH5iInd0/9Locxca2ZPmdkhACmlJyieF0cAL5vZ+WbWLfdnX5ki++CQv6DMbAZgB2BDM3vRzF6kkNVWMbNV+rGrrwLbmtkBvdS/SjH+s0JKafby32wppfYXnWcBa13KdWFqzXZOM5ulre758vN4ikHe9u9B4dE1mVsp9OVte6nvdG4/opBP1k4pzQpsUJarDZt+7gNFtOEAYWZrUrygNOXDn3/HezqlNCGl9KOU0uLAKOCHZrZxWXduSmkkxXVIwP8bolMaKqbIPjgcHtS2FHLZ8hSu5KrAchQDmrv1Yz/jgY2B/c1s3/bKlNInwKnA8WY2L4CZLWBmm3XY57zl/qY1s6+Wx3VVSulZCs32GDOb3sxWBr5FMTYGcB5wqJnNY2ZzUwSAnFPWvQTMZWaz9ePchoyU0lsUx/srM9u2tKamNbMtzOzndD63WSgeGG+a2ZzA4W27fwlYfGjOZPiINpx8zGxWM9sKOB84J6eMTOyeNrOtzGzJ0sh8m+I587GZLWNmXyyns3xA0d4fD82ZDQ1TbB8cBq30GuAXmfIdKGS9aSi056Nc3Ua4cRxaAyEWo3BX98zUTU8RcvkURYd9GNi/l+PanSKK7ySKgdnHgP9w9QtSRLe8TqHn7u3qpgdOBF4o/50ITO/qz6Bwwd+kYVF87hh3Bu6k0PhfpIigXK/TuVFIBKMponseA75Ttv80Zf26ZfkbwInDfY7Rhs36RzEG9T5FZN1bFF7AfsDUZX3Lc6As6/WeplBixpbt/xzw32X5yhTjyRPK+/fKpt6H0Qdb/8WS70EQBEEjiRnbQRAEQSOJF1QQBEHQSOIFFQRBEDSSeEEFQRAEjaS3SV2DRURktGIT36QHA9aGuQCZ1mlgBVtuuWX1eeaZi2lk//73vwHYbLM6av873/lOj+9+8sknAEw11aDZQv1tw8luv76229///ncA9ttvv6psuumKxP0ffPBBj31dccUVACy11FI99qV29L+V+81JYFj7YI7rr7+++vzwww8DsNxyy1VlSy7ZuprOm2++2ePzRRddVJVttNFGAGy++eZV2UwzzTRwBzxMbai+M7F+oPvS96Fttinyx77+ejEf+pprrqnqXnnlFQD++te/Dsjv95HsTsKDCoIgCBrJUIeZhwfVSqMtrwMPPBCA3/zmN1WZrFdZXp/5zGequrPOOguA9dZbb3IPsT8MuQfViT/96U/V56985SsArLJKnSDljTfeAGoLXh4VwEMPPQTA5ZdfXpV5D7WdAbJgh6UPvvvuuwAccsghVdkjjzwCwDvvvFOVLbroogAsuOCCVZn6oCz9J598sqqTZ+8ZO3ZsjzIpAVdfffWkHH47jfFCX321yB739a9/vSq7+eabgdZ7Vd6U+o73rqaeeuqWOoBTTjkFgB133LHX3/7443rus/bRD8KDCoIgCLqHeEEFQRAEjSQkvuGlMdLA97//fQDuuOOOqkxywZxzzlmVPftskVx69tlnB2CWWer8ue+//z7QKsfsv//+QOsA9QAHTgyqxOfvj3Yp7eSTT64+X3jhhQA89thjVZnaZtSoUVWZ5E/tV98DuOeee4BWmWqhhRYCYLvttqvKvve977Uch5dnJqFNh6UP6hx8gMPcc8/dYzvJfdNPP31VJnlOfXCaaepYryeeeKLHPlTvpUN9lgzbSbrqA4PWhp1k3FtuuQWAgw46qCr75z//CcCss85alc0777wAvPzyyz324SVmoWvy2c9+tirTfT/HHHNUZYcfXqTs23PPAVkNPiS+IAiCoHsID2p4GVYPynsAP//5zwFYccUVqzIN6CsgAmrL7L333gNaw3Xnn39+AF58sV7KS9vJshsEBtWDynknp556KlAHkUDt6XjvR4EAsj4BDjigWB3mqaeeAloDIhZYoFheTJ4B1APPzz//fFWmsPVjjjmmP6fSG0PaB8eMKVbROPLII4FWD0rh4LlAB+8lCXlSCtmH2uv3baj+6Pehz/K4TjvttKpuiSWW6OvpiCFtwzPPPBOo29D30WmnnbZHmbxPf18uskix8ob61wMPPFDVyXPyXthHH30EtHpyb7/9NgCLLbYY0Kq+iE4KRBvhQQVBEATdQ7yggiAIgkYSEt/wMqwS39e+9rXq87333gvUrj/UA6gTJkzoUSb83ArhB6M1R8XPD1pjjTUm57DbGfJ5UJtuuinQKt1JRpGkCbUs4u8xSVCSYCQNAnz44Yct+4K6fb2MNddccwH1IPlkMix9cJ999gFg9OjRVdk666wDtMpzkvFyqE1824hc4IQPwpDkLNlrk002qep+//vf9+0kaoa0DRWENOOMMwKt848kQ/sy9T/JfwAjRhQr3ku+l1wHdVCU30euL0uy01CAl6vXXHPNXrfvhZD4giAIgu5hqHPxfeoYN24cAJdeemlV9t3vfheYpNnWA4q3mmSFvvXWW1WZLHVvxWr2vqw3H2auAW8/8K39+gHUAfaghozXXnsNqC1y7+nII/Iepq6vtyIV8quQfB8Wrnb2lqs+++0UMCHL1Yf+Nh2djwI9fCYJBejsvffeVZm8HnmenlzghLwv71Vp0N9nlFh11VWBuq8ee+yx/TyToUXeNdSBSfJIfH9RYE7u2eK3U3tK4fAh5VIBfKCFkCcFMMMMM7QcxyWXXFLVyYOa3Dx94UEFQRAEjSReUEEQBEEj+VRKfP/617+AVjnm2muvBWDnnXeuyjSwv8EGG/Rr/7/73e+qz8oOoPkvADfddBNQz/sYLsaPH9+jzAc4yD33mSE00CoJwQdJSDL0gQJCCSuhHiDvNjSwrv7jB50lKfkBfrWNtodaqlt66aWBWgL22/v2kyzjZUL91n333QfAhhtuOOknNcSo3/j5dkLSXi67RC7jgeZLealP2/l+rH34st133x2oE8/ON998/TyTocUHxOg+U1/z/UXJdX2fkyTsJWkFR0jG93WSE72cp/36OZHqm+q3fsmOo48+uu8n14HwoIIgCIJG8qn0oHKDf8pT5a2xvfbaC2idWa5BSD9oKWTl+tBh7c8v/rXttttO8rEPBLK4fPi48FamzlUD+tA60Arw3HPPVZ9z4b7yMh5//PHJOOJmIG9Y1zmX9863n6x5v53aTwP23kqVd+HbUe3nB5v1+bbbbgO6y4PqhDwdn3VEg/c+UEdtrHbybS5PwHth8jT8dt3WZlrMEno+e/zfyubi+5CmQ3gvXH1SwU4e9blc6LlHnpn29fTTT/flVPpFeFBBEARBI/lUelAKj/QoR5gfQ5Cndeutt1Zlsl7lGXkLWOG+K6ywQlX2zDPPAK1hnLmszUOJvBmvU+fCQWW1eq9SllkujDVnvcoa8+M13crdd98N5Bd5Ez6PnLbLtZXqvFUr78q3lfqXH+vT9ZAH1Y3oXH3b6L7xHpT6kh+DUoi0v6eE2sb3We1D4yjdiKYU5PD9RWO93uPRGLL3qjSdRCqKny4ij8y3lyby+2ko88wzD1D3YZ+7T2NVOc+rP4QHFQRBEDSSeEEFQRAEjeRTJfHlZAUhGc+7ywoO0Ox/Xy832LvNkgd94IAGErfccsvJP4EBQsfkAx4klygwAmpZxS+poYFTyaR+H3L/fciutvcD1N2K5Frh5TnldPPnnpNNJQFKHvT9TfvzbSppx8tZ6r9+CY5uQ+3g78XllluupQ5qOc+XqS1y93FuqQ71vVxwUqdnQpPw96X6jM7V12mYwd9vkvEUUg514NdLL70EtA5V5CQ7DQf4JTt0bST1+XD3Bx98EID111+/z+eYIzyoIAiCoJF8qjyodovWhz4rz5oWjYPa8vBhwrI0ZAH7EGx5VT74IBdqPNzI8vHW0B577AHA1VdfXZXp3PzAqM5NXpWf4KdFz/zy5JpgmMul1m3IytY19db69ttvD8CNN95Ylamv+AF+9cFlllkGgEcffbSq08C+DxtWhm/lTIO6L+Umr3YLuTx66m++TgP8vq11HeQ5+O3lOfgy9ctOHlfTPSgfwt3+HPOei/qOX5VAXqLyaPrvyOPyzywFOHjPTPevD/eXeqRnob9GN9xwAxAeVBAEQTCFEi+oIAiCoJF8qiS+dpnNL4GhgUcf9KDBwtyiW+3zoaCWKLy7rIAJ74bnZm8PJbk5FcsvvzzQmvFCrnsul5ykBO/ya3svk84222xA61IHkg588EU3IOlDsuYjjzxS1V1wwQVAPTgMtYSaW3RPkk1uwUc/YK1lKXbYYYeqTLKXn2/WbeSkNZ+BRSjjgwbzoZ5HmJPltJ2/L3W9cvOgclJjE/GBVzpmSXb7779/VXf22We31EE9x8lLwupjfjuhdvJSovqaDzTREMidd94JtAb8PPTQQ307sYkQHlQQBEHQSLrDfJgI8nByYb1+tn+7B3XuuedWn2WV+YHBdm9pYiik2mcpl0fmLRU/gDkcvPDCCz3KFDauYBHIL5bX7g349hLKawi1Z6Y8dlBnUV9qqaX6fexDjfeo5UnKIvcWo6xU337aznug+o7aNjf478PMOy38lst92M2oLbQgJNQrCngPop1OCxdC7cl2s8fp8+K1L3p5/PHHV3WjR48GWj0YhYvn+pr6qL9ntX+pH1BPw1l33XWrMvXrv/zlL0DrFIvbb7+9H2fXO+FBBUEQBI0kXlBBEARBI5kiJL5OElxu/tGZZ54JtM4tkevqB6gloeSWSxB+oFbbb7rpplWZ3F6fAHO4JT7vzreX+QXJ5OJ7CUXnqzbxS3ZI5vLnutpqq7VsD63zqpqOzx6hvqH28BlGhJeill12WaBVZtZn/e/7rgImvJyj/qPZ+tAzW4KXj/12TSYnyynTgdoN6owHuUCT3JwnbefbKLeYZLcgCd0/d9RPcsmKtRCmD0BSxhG/vfqd2sYH62j7p556qiqTTLjqqqtWZXqOHXjggT32kVsMdVIIDyoIgiBoJFOEB5VDYdD+ra6yww8/HGi1BmRReI9AZd56ac+Xlkvrr9T0fh8+IGObbbaZtJMaIDSQn0uF74MeZI17y0tehDwp7wGozHtImqnuvbZuGqz22TZ07dUGCvcGuO6661q2gbrvtXvdkM9GofbzmSTOP/98oHXRTHn+anvv5XWLB5Xj+uuvB1qDPxS8M3LkyB7ba7tc/j1/X+rzH//4x6pMS843PYPEww8/DLR667ofc+qQPO6bbrqpKlMb+u3V/9SHvHKkulwGGZ/Roj1LhA9jl7c6ud59eFBBEARBI5miPChvSeUmQH7xi18EasvXh1HKWvChw7J8cx6ULI9cPjSfZVp6urckhjuDso7FZyuWZu3bUJZnTuvWeJNvZ3lJ3gPIjdN0kwflJ4i2W65+kberrroKqD1GyE/07oT27xfUVC7DJZdcsirzY6eQH1PsRi666CIgn1tP+fSgvn+9d9uOH7PKTazuFnTM3sMROY9EC696JUT3uX+OKXGA7nu/vbLF5xYeveOOO6qy3XbbreW3/XNCv+XHo/3YfF8JDyoIgiBoJPGCCoIgCBpJoyU+L43IfczJJpLKcqGro0aNqj5LblphhRWAOocU1KG9XrLSwKCXvSTtyUX28opCPJU9AWqJwi8g9o9//AOol1IYajQD3c/8HjduHNA6kJoLEpH8JJff5xiUlOJD1SUT+N/yEmDT8dLHs88+C9SyrQ8Hb1++AOp289JHu0TsZV71Nx+8ogwciy++eFWma6T9+uwV3UJO3pYc5OVM3Tc5yU73pa/r68KYCmRaZZVVgNY+3qTACQWC+OPTveeHI4SGF3L5Pv15tS8X5IOd2hfV9L91991399hve35Oz+QusxMeVBAEQdBIhtSDynk/uTJ5QrkQ5k74gdS99toLaF3m+OKLLwbqcFOfzVwBE/fff39VpgAIbxXLI1CZz5AsS85btLLUfH4xhY4Olwcla98PMqvtvKeTyxfXvgCjt5pk2Xov9OabbwZa89H5Nm46OYtc/dNPRtQ5+3NX++UmkucCZWSx+kmW6kt+ArDaWcESfmpE01E/UD+67LLLqjoNzvs217l6S1z3me7FnAfl+7HwE3WvuOIKoPagmuQ1eeTh+Gustpt//vl7bK82yWVuzz1jc1MgdL/7cH+13X333ddjf1KOfFCFgs68yjAphAcVBEEQNJJ4QQVBEASNZFiCJHIzoHN4l1QuroISlP4daqnurrvuqsp22WUXAI466qiq7IQTTgDg//7v/4BWl3+nnXYCYKWVVqrKTj75ZAAef/zxqkySw/e//32gVSaTnOflGA34esmhr/NiBgu1v5cYc3MlJDn5MslV2kdOvvKSoH7jb3/7W1Xm5w81HT9/TQPFkvG8vNlp8cXcgpcKNvH7UJvm8q75RSZVJpkmtwBlU2mfN3jOOedUn3WveDlcZX4OU/t8Ji2V47/r56/pnvXBF7pvh3tO4sTIBRnoeq+33noAXHjhhVWd7tlc8I3vh7pH1Yd8XS7Lifq3f3ZLvldOPn+s2m5y+2Z4UEEQBEEjGVIPKmdt33DDDUCrVaTlwX1GBnlQejN7j2S77bYD6rxlUFu7hx12WFX2y1/+EoC11lqrZZ8Ap5xyCtBqjSnE14cay/KVN+YHaDXD3c/wXnjhhQG49tprq7LhzmauIA3Pj370IyCf8Tjn8cm6ymXe8AOje+yxB1BnPO42/MCv+pwGrr2VKkvUB4Mo1NeXtd8DPkOA2tlbqboevp21nY4ntwBl01GbeG9Jfco/C5TjMBeMpP99UIX24e9jlem5AnXGhfPOOw+oFZemoWAD3yd0/RXYpYAPqKcoeC88lxGm/d72z6xHH30UqD1Pv70PGDvttNOAup/n9j+5WWPCgwqCIAgaSbyggiAIgkYypBKf5tr88Ic/rMrkunqpQ+65D1hYffXVW7ZbaKGFqjq5pD/+8Y+rsrPPPhtoHbyWe+pj+YXcWS9nSQr07q/kHcmPPoBCC3ytvfbaPfbrZZ6lllqqx+8PN5KJcjJsLllsbs5ObjBWS0F4yaWb8IPtktkkmfgB/9zse+HbVG2jfuTpFDzks6RofwqW8FJ4t6AgBR9kpEF2L5vfdtttQGvgkb6jeVN+vo4++/bSc8fvQ5KhApuaKvEpKMxLvBpmUF/z2R20vQ9wyAWCtM9n9H1U0qFfNkjb+6Ah3RsKsPJzANW//XNvUggPKgiCIGgkQ+pBtS8TAPUgmreCZHX7VO0XXHBBy/e8x5XLmZcL+5UFIcvLW2qyJHweOaWW99aYvB/95gILLNBjH97qVpjlgw8+2GO7JtEpbNyj85ZFlxtIndg+mh7a6/GDvPqsoBmf76zdq4G6rXJlar/cgoW5HGu5Y1K/7MZlJHQOWjgQ6rbwfUrb+UAIeVDyuD73uc9Vdddccw3QGhCx7bbbtuwL6ufNIYccMplnMrjoHH0fUjvpGecz6GhhVO9V63nqM9wom4v275ce0jPNL+iqNvZtrZyje++9N9AamKH9Te6UmuY9KYMgCIKAIfagtNS5X/JcYaRa7hlq7dN7LvJENLHRW+ne+2rHW2PSZ33YuNAkPj9+tPLKKwOtobBHHnlky/Z+cposNL9In8I+vWemsSq/ZPhwI83YWzyyiLzHp+3kfeYyyPt95Np6Yh5Wkzj99NOrz8r4Lu99v/32q+qU39D3t1w2c517bqxK5Or88tuamC4L1lu/3YIm6Pr2yqHJ9H78SJa9PAl/D2600UZAa7/M9VV9RxP+t9pqq/6fxBCg55331uVN5pQYJRwYSjQm5lUteXxeIZgUwoMKgiAIGkm8oIIgCIJGMuwLFm6yySYt//eG3FrJdH7A0y+a1wkFR/icXP3l6aefBmppIjfDfcSIEVWZwqt9WRPDzHO0L64H/V9ssFMWCj/w21R8EIz/DK2DwjrPnJyXW9JA+ECRXPCIynxY+gYbbND3E2goucUJc5Kd7jMfTCEZT8ESPkhEi0n6PJvar39m6L791a9+BTRX4pOMl5PeFd7tkcyWW6qov9J67jd9/9b9m8uMkws6mxTCgwqCIAgaybB7UH2lPf/WcKEJwFManSbS+sHY9nx73iqTdZWbmNqtdFoK3OfA08KY/nzVbjmPKOedilzZYostVn1u/673apvulSrMXp6RD1yQV+ODhxQc4Sf0yktQu/pwaOE9KP2W36/6u7w1BcDA8OfKzOHvQbWZz4sn1CdywUueTvdlbrqI9ucDIYS8YN/3Om3fH8KDCoIgCBpJvKCCIAiCRtI1El8wuGgg2bv1ymjgB0YlNUhW8lJCbsG9yXXxh5tOA8tedlMQQ25wOpcxIzfXSW2ZmzviJZ72Y+qGjBxizz33BOrsB34Oo+Q2nwVCUpzPJKGMNCrzcp6kQM2vhDqfXw4NGRxwwAFV2SWXXNLX0xl0dK1z+QZz86By92Wn/faXXL/Vc8JLzZobpaC2SSU8qCAIgqCRhAf1KURejc/59pWvfAWAiy++uCqTRest9E754jQAvsQSS1RluekDE7PumkRuMFkeol/OWtajz3CuQBIf2NMejp7zjHIekQ8z1+9qkLybAlEU6q3AhjXWWKOq0+Kl3oNUH/RlF110EVB7S75OnpC2ARg5ciTQ6oVtvvnmABx66KEAnHXWWZN8ToOJpqTkpndo2oxnsL3pnNemnIA+uER9ORcK36/fm6xvB0EQBMEgES+oIAiCoJHYEMsD3aNFDA2TMlI52W3YaQ6OT90/ZswYAMaPH1+V3XnnnQAsvvjiAKyzzjpVnWQ/nwxYc1C8DDPAEl9/27Bf7ZcLEBGSh6BOAOwDRCZMmNDje9qf2sO3i66Hl0+1vZ/Dc8YZZ7QcR6e5Wn1gWPqg8POPJIVqThnUyXq9VNw+T+l73/te9VlBGD67xI477tjjd7UchWSyyZTGhrUNW3ba4d5uONkDDg8qCIIgaCRD7UEFQRAEQZ8IDyoIgiBoJPGCCoIgCBpJvKCCIAiCRhIvqCAIgqCRxAsqCIIgaCTxggqCIAgaSbyggiAIgkYSL6ggCIKgkXzqXlBmNsbMdu+lbnEzeydXFwTB8GBmu5vZmA71V5vZN4bymIKhoSteUGb2jvv3iZm97/7eeaB+J6X0VEpp5k7bdHrBNYmharOgFTMb69r6DTP7s5ktNNzH1Q2Y2Ugzu8XM3jKz183sZjNbc2LfSyltkVI6u8N+O77guhnX3yaY2Ztl++1tZl3xbJ8YXXESKaWZ9Q94Bhjlyv4wFMdgZlN100Xvb5uZ2bAv0tSEYxggRpXtPj/wEvDLYT6exmNmswJXUrTVnMACwJHAvyZzv1NKn+rEqJTSLMAiwM+Ag4HTcxuaWfcsv0yXvKD6i5nNaGbnmtlrpVVxh5nN7TZZrLQ0JpjZNWY2Z/m9Jc0suf2MMbOfmtmtwLvAecC6wCmlhXzCkJ7YAGJmR5nZH83sPDObAOxiZtOb2Ylm9oKZPW9mx5nZZ8rt9zSz0e7705hZMrNFy7+3MrOHyzZ9zsx+4Lbd2szuLa/FGDNb0dU9Z2YHmtn9wHtDdPpDQkrpA+AiYHkAM/uSmd1jZm+b2bNmdoTf3sx2M7NxZb/979I67rni45TJ0gAppfNSSh+nlN5PKV2bUrpPG5jZsaVX+rSZbeHKR5vZnuXn3UvP63gzex34I3AKsG55z745xOc1ZKSU3kopXQ7sCHzDzFY0s7PM7GQzu8rM3gW+YFONCPQAACAASURBVGbTlW35jJm9ZGanmNkMAGY2t5ldWd6rr5vZTTLMzezg8rkwwcweNbONB/ucpsgXFLAHMCOwIDAXsC/wgavfCfgGMB8wE/DDDvvaFfgmMCuwM3ArsHfpiRww8Ic+pGwHnAvMRnEjHwZ8DlgZWA34PPCffdzXmcC3SktuZeAGgFKiORXYk+JanAFcphdfydeALcrjmGIwsxkpHha3lUXvArsBswNfAvYxs23LbZcHfk3Rx+anaIsFhvqYh5HHgI/N7Gwz28LM5mirXxt4FJgb+Dlwulmva0qsDTwFzAvsAuwN3Fres7MPzuE3h5TSHcBzwPpl0U7A/wCzAGOA/0dhEKwKLEnRzw4rt/1R+d15KJ6PPwaSmS0DfBdYs7zHNwPGDva5TKkvqI8oOvKSpTV2Z0rJBz+cnlJ6PKX0HnAhxYXqjTNSSg+nlD5KKf27w3bdyJiU0hUppU9SSu9TPByPSCm9klJ6GfgJxQu6L3wELG9ms6SUXk8p3V2Wfxv4dUrpH+W10GJGfmzh/1JKz5XHMCVwaWmpvw1sCvwvQEppdErp/rK976PwyDcsv/MV4IqU0piU0ocUD4xPzVIDKaW3gZEU53wq8IqZXW5m85WbjEspnZpS+hg4m+IlPl9+b4xPKf0ypfTvKahP9ZfxFFIpwGUppZtTSp9QSKZ7AT8o79MJwNEURiIU9/H8wCLlM++mVCx58TEwHcU9Pm1KaWxK6cnBPomuf0GZ2dTWGhAwAjgLuA64oHRJf9amRb/oPr8HdAqMeHbgj7oxtJ/b/MA49/c4+m7FbwdsDTxTSi5rl+WLAAeXksGb5YN7/rb9TmltvG1pqU9HYXXeYGafNbO1zezvZvaKmb1FYdlLeh6Ba4fSeHptqA98OCkNwd1TSgsCK1K0iWT0F912koJ7u2+ntP40KSwAvF5+9u0xD4W6dJe7H68py6Ewpp4ArjWzp8zsEICU0hPAAcARwMtmdn75rB1Uuv4FVVrlM7t/41NKH6aUjkgpLUdhlW1H4R1M0k9M5O9upv1cXqB4oYiFgefLz+9SdGzx2ZYdpXR7SmlrClnlSuD8supZ4MiU0uzu34wppQs6HMcUQdk3L6awPkdSyKmXAwullGajGBuRTPUChSQNQDkmMBefUlJKj1AYmitOZNPs1yfy9xRNKasvQCHnQev5vwq8D6zg7sfZFL2cUpqQUvpRSmlxYBTwQ401pZTOTSmNpHhGJAqpcFDp+hdUDjP7YjlAOBWFzPIRxUNiIHgJWHyA9tU0zgMOKwdK5wH+GzinrLsXWNnMViofnofrS2Y2g5ntZGazppQ+AiZQt/dvgf3MbE0rmNnMRpnZTEN3WsNDeb7bAHMAD1OMAbyeUvrAzNaiGBsQFwGjzGy9cnzuSCZtKfGuxMyWNbMfmdmC5d8LAV+nHr+bHF4CFmwb95ziMLNZzWwrCuPwnJTS/e3blDLfqcDxZjZv+b0FzGyz8vNWVgSLGcWz82OKscFlyufqdBTj+e8zcM/UXpkiX1AU0sDFFA38IIXcd94A7fsE4Oule3zcAO2zKRxJ8SK6H7gPuB04BiCl9BCFVj2aYrD6xrbvfgMYZ2ZvA9+iHLtKKd0O7AOcDLxBMRi+yyCfx3BzhRUTvt+mGJz+RkrpQYpgnZ9YETV5GFB5kWX99ygeLi9QvORfZjLDrLuICRTBDbeX0Wa3AQ9QDNpPLn+jeA68aGavDsD+msYVZZ96Fvgv4DiKQLHeOJhCxrutvF+vA5Yp65Yq/36HIiDs1yml0RRy9c8oPLAXKZSSHw/4mbQRS74HQQMxs5mBN4GlUkpPD/fxBMFwMKV6UEHQdZTS54yl/HkshSc7dniPKgiGj3hBBUFz2IYiPHg8hdTytRQSR/ApJiS+IAiCoJGEBxUEQRA0kqFOpDio7tpVV11Vfd5yyy379d233noLgOuuu64q23777XvdXp5n79lW+sSkfHlQ23DMmDrp8wMPPADAdNNNV5VNPXWRa3LppZcG4L336vR5b7zxBgAjR47sUfbZz9bTpmaffUCzzfS3DfvVfl5haL/WH374YfV53LhifvMnn3xSlb3+ejFP8u23367KPvroo5Z9+O2nmWaaHr8z00xFNP5iiy1WlU077bRAa5u28+9/10lPtN9eaFwf7EIa14bHH3989XnChAkAHHdcHXS8zjrrAPDlL38ZgCefrJNCfOYzRTS+7l2Auecu5pPvu+++Vdm88847kIecbcPwoIIgCIJGMtRjUJP9Y3rT/+IXv6jK7rrrLgCefrqOxtUbXxY/wCqrrALUVuvDDz9c1b36ajE9wrfHUkstBcByyy1XlR1zzDEAzDbbbC37Aphqqn6/7xtneX3729+uPl9//fVA6/mr/VdcsZjgP8sss1R1stR32223qkxexvTTT1+VrbfeegN5yIPiQXXykK+55hoAnnnmmapMn+VJAbzzTpH+0fcR9Ud5Qd6j0m+pDuo+5dt59dVXB+r+ufji9bzxRRddtNdz8bjzGpY++O677wLw5z//uSp76qmnALj55purstVWWw1o7YNjx44F6rZbc806reP48eOB+hoBzDNPkcVH7QYw33xFGr8vfelLwCTdu57G3Md33nknAOuvv35VttNOxXxwr4ScfPLJANx00009ttdzctNNN63KTjvtNAD22Wefquzoo48eyEMPDyoIgiDoHuIFFQRBEDSSrpH4br31VgC++c1vArWbD7V8NOuss1ZlkpvmnHPOqmyuuYrcmx98UCwN5QfrJUVJZvDflZwH8IUvfAGA/fbbD6gHsaGWcvohFzRGGhDf+c53qs9qV3+Okl+WXXZZANZaa62q7p///CcAq65ar14iOc+3yTLLLMMAMmASX6eACIDzziuyZUnmfPbZOkn0ffcV6+rNMMMMVdkLL7wAtPYzySf/+Mc/APj4457pzBRcATD//PP32K9+X8EoPiBIZT6oYiIBPUPaB9Umxx57LABzzFEv+7TIIkWe4jffrNcUVLCHD0i55557gDr4xMtTwkunkvNyx/H++8VqHD/4QbW+Zsfgk15ozH380EMPAbDxxvVagnou7rxznS9b/e7ll18G6kAKqNvzzDPP7LHf00+vF+r96le/OpCHHhJfEARB0D0MdZh5r+SsVw0yAzz/fLHqg6ynV155papT2SOPPFKVff3rXwdqr8nvV4EOfhBQVr28K4ARI4rlTnyY7gUXFPk999hjj5a/YbIHWocVhZdrQBnqUFR5RlBbo7lznXnmmXvUKQx9EqzSISfXB72XpEAa9QcN4EMdHLHDDjv02N4HiOy///5A7S34IB711X/9q84Pq4AJHzihAKB7770XaL1m8va9B6VzmZiHOBQoKEIBHt47V3v5Y5eX5D2ir32tWFtPnoFXPV58sVg2asYZ65VhFl54YQBeeumlqkx9W9ft8ssvr+p8oFC3IRUnp4z5MPOVV14ZgAUXLFZ48e2r4Affb9VPvac1FHTvEzUIgiCYookXVBAEQdBIGi3x+XlNt9xyCwA33lgsQ+QH6LbeemugntMAtUvqJTu5rLvsUixH5OUbySRe+tBcDT8wqEFrDRpKloBaemmClNJf1L5+gF6ZJLz7L+lE56U28nW+zRXM4qWsBRbo6yryQ4OuV0629LKQpCRJUD4oR7Kcl1EWWmghoDXAQRKf2sX3Ff2+l42/+93vArDEEkv0+C3JhF4Kl8TV6Txh+CU+BRv5bATqSz5IQlkNvMQpaVN9ykuckvN8cJT254NV1EfVDgpygTowYyIZOBqNn3snfFs/9thjQD1vyrevAlf8Pat28s+7oSA8qCAIgqCRNMZEyFl0Prz785//PFAPuitcF2rL0Fu7spZ8OLoGZDUY7S1g/f5rr71WlWm7UaNGVWV//etfgTp82nsc8qC6kQcffBBoDSoR3iNSRgNZu8phCLUl6wdSdW2a5jV5FHKbs5iVmQDq/qWsBr7PqmyDDTaoypTh4KijjqrKjjjiCAAOPvhgAM4999yqTiHPJ510UlWmPus9VW0nfACKAlU0LQNgySWXBFo9jQHKJdknfECTMl0oz5v3WpXf0XtQOk4fTLH88ssDdSaYXN/y11LPAh+q7vMjQmu4u0LQ5QF3E/Kc/PQFKSDeg5ZXLw/Ve0vC53PMPWOHgvCggiAIgkYSL6ggCIKgkTRa4lMgAtRznZ577jmgVVqSy+/nQWkOk1xYqAcJL774YqB1QHnbbbcF4MILL6zKFEShWf9QSwGSH3/zm99UdUpg2y2BER65+F6mlFzkgyQk8T3++ONAq8Qp2dXLqpKVvLzSBHLBMx5JvX5gXf1HEqaXTCQpecnqoosuAlrbSBKf8IPzCojwbXXYYYcBrYEWkqaVBcDLLsoq8cUvfrEqO/vss4HWOVqSb/zg+GChe9ajQA8fqKRj8XKbPvs20TXJSXC6333giK6Jl70U8KL9+32pPbtR4lOgkpc41U9zsl9ujlyuvVTvl+AYCsKDCoIgCBpJYzwoj6w7DSRDPdCrAUxlg4DaSveDpcoM4cMiZRVrprgfeBXrrrtu9VnZFWSBQh1MsNVWWwF1yGu3I69AM8uh9kJ9G8q6/NznPgfAr3/966pO7elznyksv2l4r0lBBz5gYc899wTqZQagDmFuX3QQauv/xBNPrMrURvLYAa688kqgDjffddddqzotHnf//fdXZf/1X/8FtHpm8nblVdx9991VnQJ65I1B3hMYCs9JeGVD56HMMD5QSV6N7z8KDvH3qjxSLR/hF83U9t6rlJfgvdD2wX6fvULZJXT9uolcNpdcjlD1oVwuyCYRHlQQBEHQSBrpQUk/9dZr+0JkPtRWlkEuS7YfQ5DeLetNYa1QWxKPPvpoVaZQVL8InRbq22uvvYB6wS/ovgl+3hPQZ7/4nULO/fnLS91www0B+O1vf1vVtXtXUGvXuXGepqDxR98emk7gPeof//jHQB0q7a16Wed+jElh0PKaAA455BCg9gL85Ellm86F8vpxTbWpxgP9OI6u1f/+7/9WZaeeeipQT8oE+N73vtfjNwYLTQr1yEtUTjyoz8eHmcvSzy36qGeC9wZ1TXx7aVzKh+NrDFJjqRrHhtbcft2Gxt58Pkfde95b6jRO3mmBy6EeXw8PKgiCIGgk8YIKgiAIGkkjtahcSKNkOYWG+/T4yq3nQ6Q1WOqlJS2kJxfeZzxQeKYfcN1kk02AVhnroIMOAuolKPxxSK7olowSXkqRTOpnj0sS8EESynco+c+H+yuowssAGsjX4G1T8BKxpCJ/jAcccABQ5yOEWkpTIInCvKGW7HzmCfGTn/yk+qyBfb9AnlBQjpe9FODgB7j1WX3byzn+mgr1Xy+TDaXE5+9jnb+kKJ8hQ/isBvrsz1/9Us8JH/yge9qHquu3/JQTyfAKctISHtDant2G+mQu+MFLd6rP5ezLbd/+vaEiPKggCIKgkTTSgxI+5FnBCRpw9tbrJZdcArROTlSAhbcojz/+eKAe7PYZj5VDzYeUazDce1XyEmRJ+KAChbF3iwfl8w7KsvVWk8q81dS+8KAfoNf23nqVheY9sybgz1NBCd7S14C9n0gra15evA9NVpnPqL/GGmsA9VLxAJdeeikAe++9N9Bq/Wtiup9EnBuU9p4ATHzwe8cddwTqwI+hJpfxXp6O95Z033hlIxdmrvOXp6NJ/FDnRPT3rLwv9U/o2U5+MvFQ55sbSNQmffV0dB/4+yHnOYlO2fIHg/CggiAIgkYSL6ggCIKgkTRS4ttpp516lCnPmxYx9MtCaOkLLeAGcOSRRwKtyw5oUPmEE04AWmUALQjn56VIathjjz2qsmOPPRaoJQIvL1x99dUA3HDDDRM9xybwxBNPVJ/bZROoMwB0ykmmheegHoz2A6+aS5ZbxmM4kdQE9dwuL00qkOa6666rypT1QNlMcksUSAKGWrLTnDGo5/Epv6Pvn8ouoSwlUC8z4zMutM8p89KVtlNOPoADDzwQgMsuu6zH8Q4muvaSS6E+Vkl3Psee5kt5GWnllVcGWueoqY+qn/m5i5JVfWCPhgN8G+r65wKyJAn6JTn8d5uMnlkTk/jaF+fMBUvkck2q7w8V4UEFQRAEjaQxHpS3eLTQ2z777FOVnX/++UC9mNtaa61V1SkE3WeNVviztwyUZVuWsl/ATay22mrVZ4Ud//73v6/K5GHJ4tIANMDmm2/e6RQbh7caZSH5UGtZtD4QpB2fNUKD+34fzzzzDNDsTBI6NuXagzq/nV9sT9ajAhu8NakgEGUwB7jrrrsAOPTQQ6sy9VG/sKE444wzgFavXGHrPjuJ+q+8NR/arsCiXKCBMmYMFepffjUAKRWyzv39qRx8PghEZd7T0nfUDj4QSnU+wEr78x6BAqA0jcDfC9qvL+sWDyoXti/8+UsBkqfl789crkl5XBEkEQRBEATECyoIgiBoKI2R+Pw8Gc158HNEDj/8cAC22247ADbeeOOqTgOePsDhnHPOAVpn5WswXPKfl03k6vrB89tvv73lewA333wzUA+iH3fccVXdsssuC8Bf/vKXqmyzzTbr7ZSHHe+uK8DESxmSiTS3JIffXolKfbtKGvAD5U1DAThe0pEE4ufESNKT7OSDE5SU+Bvf+EZVpmuvgB2ArbfeGqgDge64446qTsty+OwkCpLwc+s0N0tL0Hj5SzKrvwYKdtFSMUOFZHs/d059Tufjg2fUhu3zvKB13pKCUxT84LOC6JnhnyeSnH0bKtBC7eX3obbzww4+AKvJ5BYGzQVAqD07ZZLItbkPHBkKwoMKgiAIGkljPCif80zLFORmN8u78gN5Cuf1g9x60/sB5PZF2nyYtaxRbzUoOODGG2/scbzKSuFDsLttiWjvMWi5AR96rzb3nmk73gJWAIAPcZXVmgvJbgpanPB3v/tdVabj9kuNqE/pf78Uh/CZJxQg4oNG5B2cfvrpQH7gWgP4ANtssw3QGkqtACHdA95bmm222YDWbBT6Tb+woTKADGaf1bQDH3p//fXXA7Xn7etyi+hp0N9b+u1ZIHzfklebW7LDexcq0/8+GEaKifequoW+ejjtS71PLMxc7eSfD0NBeFBBEARBI2mMB6XM4e2fhc/5BvCd73ynxzbKMA61d+StLVnF0v19KO5SSy3VUgf1omreKpbX8c1vfhNoHbPqNvyxa7FHTYSGWsfPLZanMp/PUOH+3ruVRetzqTUNhcr//e9/r8o0luHHQdutR2+R5xaKU1lu2fucZ6Bxuj/84Q9VmfqZb2d5u/IS/HHo+vjj0H798WsyuVYCGAz0e36cUha++ohfKLD9Hof8cuW6b1Xm+5b6pR+DUpt470Jh6Nree0s6Xv986BZ8fk2R85LkEXXKu+fp7/YDRXhQQRAEQSOJF1QQBEHQSBoj8eXwg6VyMSUNrLTSSlWdQs8vuOCCqkzLbfgZ0pLnFLrrgyYUUpqbba/MFp6ctNcufzUdL71IytLAPsDIkSN7fKf9HJUZAOqB+dyieU3DS0AKMlAuPICDDz4YaM1IoDaSHOQlIAUiKC8k1IPtyoICtQyt5R18KPNuu+3Wsi+oZWkfqq1jV3v74CBlQfBynq6zv5+UrWIwJT61jw/Hl4yntvT3kSQov30uuEbfkRztr4NkP9+GOm9//vqs4AgfLKJgH5+bsVvIZZLoJMvl6nQdOgWmQC0j++s10IQHFQRBEDSSxnhQuXDb9oy7vs6H4mrirc+jp8FCP4CscN/2cHNf5gdcZb1tv/32PY6zPZeVL+sWD8qHJ8tq9OHJsnb9ZOf2QWvflvKmNDEUautq7bXXrsqaEFjiz13X1FuC8qBOPvnkqkzHLe9EuQqh9lL8xG15Xz74QtnR1bd8MIMW0lTOSIDDDjsMaLVmdey5KRdSCfwUAu/lCk3lGEx0nJqA6z/Lw/H3j9rX90H1M99OOm9dLx/IIrwHqf16r7l9Ac1ctvTchOGm00m9yD1PcwEUOa8q90yT9+8TGQw04UEFQRAEjSReUEEQBEEjaYzEl3Mhc2VyP737LSlBGSWgdju9WytZRa6pXyxOg9E+O4CkQ7/chKQA/b7ff7dIe8IHkGixRS9z5RYnax+0Vj40qNt1hRVWqMo0h0wZDrqFo48+GmiV+DSfSIPyfnkXSSs+G4VkJp/P76CDDgLq9vD5EHOZKZQJZbHFFqvK2vPH+WwpuflYyvbh5WttN5joGLycquAmzUnydcJLTJLovQSl81dAgN+Htvf7aJfzoL6Wkj99X1fQSac8dU3F98m+0N8ACk+npT0GivCggiAIgkbSGA+qr2hQ3gc/LL300kBrxmzN3vdWkAaO5Tl461WZyL1VoIFvLSMNtYWisN/c7OxuwXs1sjJ9yK7P/izavUTvhSl0Wct0Q51rrcneZW56gD777APKtqE28tkH1G8uvfTSqkx557yHo0Uyb7nlFqB1efc777wTgPXXX78qUzCQD0ZpX6bc91l59v7a5sKsc57LYNEpB54/Lx27v6fk6flj132uc/BqigIickue+8AJHZMy0z/55JNVnfqsFJRuQn0yl/0lh+77iXlLufs3lzl9oAkPKgiCIGgk8YIKgiAIGkmjJb5cJgmhJRIA9t13X6DVTZdLusMOO1RlSiCroAcliIV6fsa9995blUm+uuiii6qyzTffHGid2d+t+Pkpkon8/DIvgfZGbkDbS1qaod9kiU/9zAe8aHkLf9xatC63UJ5kJy2sCfXihKNHj67KtL9DDjkEgK9+9atVnZLWHnPMMVXZoYceCsCKK67Y47cUhOAThEqC9sllFfji5/oMRf+VFJobTFdf8fN21P65oAYv40kC1P0+sXl1ufmJuuZ6rvh9qG4oJKyBRpJ0bs6Tp325jUmR+PR88H1zoAkPKgiCIGgkjfSgOr3NFWLqLURliPCz57Wk9kYbbVSVaWlvWQM+qEKWnM+lJgvKD65qoDx3rN2Wi8+Hzyv7g8895wMgesNbarJCveU5lIPxk4oG6n3o9aabbgq0Lncvj0DBM7595MX481XAxIUXXliVyROQl+Rz4cl71zIvUIe7+zBo5YhTMIq/BvKW/HHLU/aL8imwaDBReLtfal7Hp3Bzf8+qXXPBDD5bhD7rvvfXTfdgrt95FUbPER2HX6rnqaeeAmq1pJtQ2/lnUG7JknYmlhEnFwDWF4VlcgkPKgiCIGgkjTRvO+Xik9XqJzX+8Ic/hP/f3v3z0vJFYRx/7uvQegMiWoVCgkhIFDqVTuIFqFAjNFQSpUKBhkpBo6DSaZB4H7d6Zp45tj/Jddx97v1+qpOZn9+dM2fO2bPWXrO2pMXFxWZbLiVtvpPwXezt7W2zz/n5jIhcEuy5AentMtCDECG8J5dyL3Xo9l1TbsuoU+pGS96X5bn97HT8XQ4PDyVJa2trzTbPN+XchM+Dy+/zWvG8W2luJ+dBexcvzPnNUmm05wTzbtU9Ev1dcKm01D4YneXxPu7scZfXdL/4uDIi8nyUsxmlDuMZmeYxm+eoSg/Se16u9NuR31WfTz+Um/+Or+maF9l8j89vKYvzUb+9Unf/zx6hyYi8X4igAABVYoACAFSp6vxUKUx1Ki5DeD+Bn6kOh/CZcvEicZ68zSf2nQY5Ojpqtq2srEjqTsJ6kTRPVJeWCRkUmcLwBPXr62uzzd0IPGkstakZyxRfaUK7tLRJDba2tprXZ2dnkrodMJwqyZSuJ+WdAvH1JLUp5TxXdn5+3rzOMn6pW/qdxQT2+PhY/DupLZxwSbzUXr/5/nr7/0ndDhb94ushCzIuLy8ltd+9TC059Z6FE/6eZSm9v4++tpyOlbrpRPN3NNO1/n94W/52OIWb/QwHhfth/klXG6f2Pvs9I8UHAPhvVR1BlaIT3xlkF213Mc9Ovi5Dz07Sngj1XUYWSbgcPSePT09PJXXLfv36+Pi4c1yDzlFlFjX47tJ38dLbCCojJJ/r0gPAtZmYmGheX19fS+pGg71d66X2Lj6XaTff6efy6+Pj45LaTvFSG13Oz89LksbGxpp97gfppd+ltuy/tHiez3f2TPTDwfmZ7e7uSuoWZPwE32FnIYSvM5+vLOZwsUNeU6USaUdJPidZuOPPsNS7MIsk/Pvg35Msunp+fpbUjeQGhaNJF9JIH5fe9/43KaPbUlRFmTkA4L/FAAUAqFI1Kb6vFhs4nZeT13Nzc5LatJvUhvC50JsLAZ6eniRJNzc3zb7p6WlJ3YIId5fISdjSsyr/Ak8SlyaGSyktK7X1zwnar3Sj+BtGRkaa1z7GTDf5WnH/Rql9bswFCKurq80+p53y+nh4eJDUffbJqRKn+nLi3tdspqd8HPmcjtNdTreur683+3Z2diS16WmpnHr9CX5v2fXFqXQXbJSuj0xF+Xy6p6PUpg6d2stiH1+/pd59uc3XrdO2TjnmvlJatXZZdGO+nnKfz/FHRUx5Lfuay88r+yj2CxEUAKBK1URQHy3vnvt9p7+9vd3s811mTsi/vLxI6k7keQLVd555R+k7VEdXUrscdN41ZBn2v8Tv9eLiotnmCX9PGpdkqbWjiDxHw8PD33qc/eB+eNlJwsUiWd59dXXV+buZmZnmtd9zXj+OyErLq2d3DvP5zpJqR6N5rbp/nLMD+Zk5msgO6vbR6gD9MDs7+2ab7+I3NjYkdcvC7+7uJHULdfzdy0jTx166Ph0tlTqiZxGMIwJ3AMlHI/b39z95Z/Vyd42MQv3bltvye/uevPb9OWUU5v6d/UQEBQCoEgMUAKBK1aT4vsoTrvf39802T9ZNTk422xy6Z3rFIatTCfmMlNMkOWno4gA34JS6y1H0GrTlNtLU1JSkbqGAz/XQ0NC7f5fLj7jQJAsQRkdHv/U4+8HHfXJy0mxbXl6W1F1+pVemnbz4ZS6C+VNKy0JkOstprxq6evgYNjc3JXVTcX7GMFN2pSVvertFZDGD04Pu+pH78/Ny/uLqDQAAAL1JREFUhxmntrNIYpAtLS1J6jbL9jnJZ//29vYktc99ZuNodyNZWFhoth0cHEjqft/z2bF+IYICAFTp12dL/QIA8DcQQQEAqsQABQCoEgMUAKBKDFAAgCoxQAEAqsQABQCoEgMUAKBKDFAAgCoxQAEAqsQABQCoEgMUAKBKDFAAgCoxQAEAqsQABQCoEgMUAKBKDFAAgCoxQAEAqsQABQCoEgMUAKBKDFAAgCoxQAEAqsQABQCoEgMUAKBKvwFZJsYxLR9A8wAAAABJRU5ErkJggg==)]

二、模型构建

1、基于上面的数据进行模型Sequential序列

# tf.keras.models.sequential()
model = keras.models.Sequential()
model.add(keras.layers.Flatten(inpput_shape=[28, 28])) # 展开输入的28*28的二维矩阵为28*28的一维向量
# 添加全连接层（神经网路中上一层和下一层全部一一连接）
model.add(keras.layers.Dense(300， activation="relu")) # activation激活函数
model.add(keras.layers.Dense(100, activation="relu"))
# softmax ：将向量变成概率分布 ，x=[x1,x2,x3]
#. y = [e^x1/sum, e^x2/sum, e^x3/sum],sum = e^x1+e^x2+e^x3
model.add(keras.layers.Dense(10, activation="softmax"))
# relu： y = max(0, x) 谁大输出谁

# 目标函数 y ->index, 如果y是输用sparse，向量的话不用，y数->one_hot->向量
model.compile(loss="sparse_categorical_crossentropy",optimizer = "sgd", # optimizer：模型的求解方法，也是目标函数的调整方法，就是选择优化算法，发展历程
#SGD -> SGDM -> NAG ->AdaGrad -> AdaDelta -> Adam -> Nadam 
metrics = ["accuracy"]) # accuracy 其他指标
# 调用model.compile的目的是将损失函数，优化方法和其他指标添加到图上，并固化下来

# 另一种写法
model = keras.models.Sequential([
 keras.layers.Flatten(inpput_shape=[28, 28]),
  keras.layers.Dense(300， activation="relu"),
  keras.layers.Dense(100， activation="relu"),
  model.add(keras.layers.Dense(10, activation="softmax")
])
  model.compile(loss="sparse_categorical_crossentropy",
              optimizer = "Nadam",
              metrics = ["accuracy"])

2、查看模型的层数

model.layers

3、model.summary

查看模型架构

4、训练模型

history = model.fit(x_train, y_train, epochs=10, validation_data=(x_valid, y_valid))

5、查看history的类型

type(history)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-MwWQOtQb-1575541836689)(/Users/bobwang/Library/Application Support/typora-user-images/image-20191203114646650.png)]

6、查看训练过程

history.history

7、画图

def plot_learning_curves(history):
    pd.DataFrame(history.history).plot(figsize=(8,5))# figsize 图的大小设置
    plt.grid(True) # 网格显示
    plt.gca().set_ylim(0, 1) # 坐标轴的范围
    plt.show()
plot_learning_curves(history)

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-W3px9IBp-1575541836690)(/Users/bobwang/Library/Application Support/typora-user-images/image-20191203114809481.png)]

8、使用测试集查看模型成功率

model.evaluate(x_test, y_test)

分类模型之数据归一化

一、数据归一化的目的

数据归一化就是将数据的所有特征都映射到同一尺度上，这样可以避免由于量纲的不同使数据的某些特征形成主导作用

二、数据归一化的方法

1、最值归一化

最值归一化的计算公式：

特点：

可以将所有数据都映射到0-1之间，适用于数据分布有明显边界的情况，容易受到异常值(outlier)的影响，异常值会造成数据的整体偏斜

2、均值方差归一化

计算公式

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DPksExpG-1575541836692)(https://images2018.cnblogs.com/blog/1376938/201807/1376938-20180718211654909-1907604593.png)]

特点：

可以将数据归一化到均值为0方差为1的分布中，不容易受到异常值(outliter)影响

三、实例

代码：

1、导包

import matplotlib as mpl
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import sklearn
import pandas as pd
import os
import sys
import time
import tensorflow as tf

from tensorflow import keras

print(tf.__version__)
print(sys.version_info)
for module in mpl, np, pd, sklearn, tf, keras:
    print(module.__name__, module.__version__)

2、数据的获取

fashion_mnist = keras.datasets.fashion_mnist
(x_train_all, y_train_all), (x_test, y_test) = fashion_mnist.load_data()
x_valid,x_train = x_train_all[:5000],x_train_all[5000:]
y_valid, y_train = y_train_all[:5000], y_train_all[5000:]
print(x_valid.shape, y_valid.shape)
print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

3、归一化

# x = (x - u) / std  (均值方差归一化)

from sklearn.preprocessing import StandardScaler

scaler = StandardScaler()
# x_train: [None, 28, 28] -> [None, 784]， 
#1）归一化的时候，所有的均值方差都要使用训练集的均值方差，所有用fit_transform记录下来，以供测试集和验证集使用而达到一种理性的结果
#2）归一化需要做除法，所以要将int转为float32
#3）fit_transform要求是二维向量，而原来的x_train是三维向量，所以先转为二维，
x_train_scaled = scaler.fit_transform(
    x_train.astype(np.float32).reshape(-1, 1)).reshape(-1, 28, 28)
x_valid_scaled = scaler.transform(
    x_valid.astype(np.float32).reshape(-1, 1)).reshape(-1, 28, 28)
x_test_scaled = scaler.transform(
    x_test.astype(np.float32).reshape(-1, 1)).reshape(-1, 28, 28)

4、构建模型

model = keras.models.Sequential([
 keras.layers.Flatten(inpput_shape=[28, 28]),
  keras.layers.Dense(300， activation="relu"),
  keras.layers.Dense(100， activation="relu"),
  model.add(keras.layers.Dense(10, activation="softmax")
])
  model.compile(loss="sparse_categorical_crossentropy",
              optimizer = "Nadam",
              metrics = ["accuracy"])

5、训练模型

history = model.fit(x_train, y_train, epochs=10, validation_data=(x_valid, y_valid))

回调函数

一、Tensorboard, earlystopping, ModelCheckpoint

# 第4步构建模型后，训练模型前
logdir = './callbacks'
if not os.path.exists(logdir):
    os.mkdir(logdir)
output_model_file = os.path.join(logdir,
                                 "fashion_mnist_model.h5")

callbacks = [
    keras.callbacks.TensorBoard(logdir),
    keras.callbacks.ModelCheckpoint(output_model_file,
                                    save_best_only = True),
    keras.callbacks.EarlyStopping(patience=5, min_delta=1e-3),
]# patience连续5次前后模型训练的差值小于设置的阈值min_delta，就关闭
history = model.fit(x_train_scaled, y_train, epochs=10,
                    validation_data=(x_valid_scaled, y_valid),
                    callbacks = callbacks)