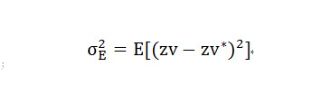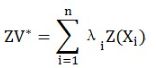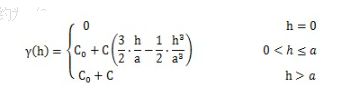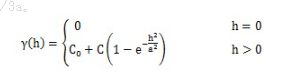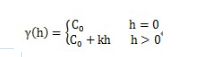一、克里金插值法介绍
克里金算法提供的半变异函数模型有高斯、线形、球形、阻尼正弦和指数模型等,在对气象要素场插值时球形模拟比较好。既考虑了储层参数的随机性,有考虑了储层参数的相关性,在满足插值方差最小的条件下,给出最佳线性无偏插值,同时还给出了插值方差。
与传统的插值方法(如最小二乘法、三角剖分法、距离加权平均法)相比,克里金法的优势:
1、在数据网格化的过程中考虑了描述对象的空间相关性质,使插值结果更科学、更接近于实际情况;
2、能给出插值的误差(克里金方差),使插值的可靠程度一目了然
插值方差:就是指实际参数值 zv 与估计值 zv* 两者偏差平方的数学期望:
而插值点的 zv*,通过N个离散点获得;
其中λ与N个离散点指的是加权系数; *变差函数的理论模型*
变差函数与随机变量的距离h存在一定的关系,这种关系可以用理论模型表示。常用的变差函数理论模型包括球状模型、高斯模型与指数模型(还包括:具基台值线性模型、幂函数模型、无基台值线性模型);
1、 球状模型公式:
2、 高斯模型公式:
3、 指数模型公式:
4、 具基台值线性模型:
5、 幂函数模型:
式中: 为幂指数;不存在基台值。两边取对数得ln(γ(h))=αlnh,线性化为γ(hi)=b1X1,i
6、 无基台值线性模型:
式中:k为直线斜率;不存在基台值和变程,当h>0时, γ(hi)=b0+b1X1,i
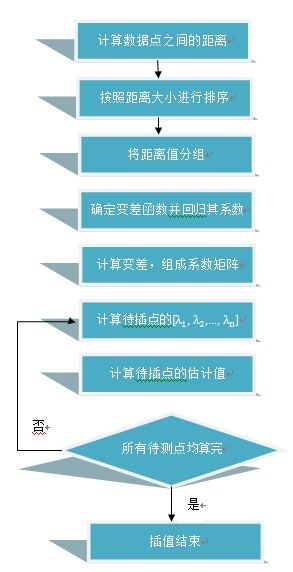
普通克里格方法的基本步骤如下:
二、算法实现
代码实现:
from gma.algorithm.spmis.interpolate import *
class Kriging(IPolate):
'''克里金法插值'''
# 继承 gma 的标准插值类 IPolate。本处不再做详细说明。
def __init__(self, Points, Values, Boundary = None, Resolution = None,
InProjection = 'WGS84',
VariogramModel = 'Linear',
VariogramParameters = None,
**kwargs):
IPolate.__init__(self, Points, Values, Boundary, Resolution, InProjection)
self.eps = eps
# 初始化半变异函数及参数
self.VariogramModel, self.VParametersList = GetVariogramParameters(VariogramModel, VariogramParameters)
self.VariogramFUN = getattr(variogram, self.VariogramModel)
if self.VParametersList is None:
self.VParametersList = self._INITVariogramModel(**kwargs)
# 调整输入数据
if self.GType == 'PROJCS':
self.Center = (self.Points.min(axis = 0) + self.Points.max(axis = 0)) * 0.5
self.AnisotropyScaling = AnisotropyScaling
self.AnisotropyAngle = AnisotropyAngle
self.DistanceMethod = cdist
else:
# 方便后期优化
self.Center = np.array([0,0])
self.AnisotropyScaling = 1.0
self.AnisotropyAngle = 0.0
self.DistanceMethod = GreatCircleDistance
self.AdjustPoints = AdjustAnisotropy(self.Points, self.Center,
[self.AnisotropyScaling],
[self.AnisotropyAngle])
self.XYs = AdjustAnisotropy(self.XYs, self.Center,
[self.AnisotropyScaling],
[self.AnisotropyAngle])
def _INITVariogramModel(self, **kwargs):
'''初始化参数'''
if 'NLags' in kwargs:
NLags = kwargs['NLags']
initialize.ValueType(NLags, 'pint')
else:
NLags = 6
if 'Weight' in kwargs:
Weight = ToNumericArray(kwargs['Weight']).flatten().astype(bool)[0]
else:
Weight = False
Lags, SEMI = INITVariogramModel(self.Points, self.Values, NLags, self.GType)
# 为求解自动参数准备
if self.VariogramModel == "Linear":
X0 = [np.ptp(SEMI) / np.ptp(Lags), np.min(SEMI)]
BNDS = ([0.0, 0.0], [np.inf, np.max(SEMI)])
elif self.VariogramModel == "Power":
X0 = [np.ptp(SEMI) / np.ptp(Lags), 1.1, np.min(SEMI)]
BNDS = ([0.0, 0.001, 0.0], [np.inf, 1.999, np.max(SEMI)])
else:
X0 = [np.ptp(SEMI), 0.25 * np.max(Lags), np.min(SEMI)]
BNDS = ([0.0, 0.0, 0.0], [10.0 * np.max(SEMI), np.max(Lags), np.max(SEMI)])
# 最小二乘法求解默认参数
def _VariogramResiduals(Params, X, Y, Weight):
if Weight:
Weight = 1.0 / (1.0 + np.exp(-2.1972 / (0.1 * np.ptp(X)) * (0.7 * np.ptp(X) + np.min(X) - x))) + 1
else:
Weight = 1
return (self.VariogramFUN(X, *Params) - Y) * Weight
RES = least_squares(_VariogramResiduals, X0, bounds = BNDS, loss = "soft_l1",
args = (Lags, SEMI, Weight))
return RES.x
def _GetKrigingMatrix(self):
"""获取克里金矩阵"""
LDs = self.DistanceMethod(self.AdjustPoints, self.AdjustPoints)
A = -self.VariogramFUN(LDs, *self.VParametersList)
A = np.pad(A, (0, 1), constant_values = 1)
# 填充主对角线
np.fill_diagonal(A, 0.0)
return A
def _UKExec(self, A, LDs, SearchRadius):
"""泛克里金求解"""
Args = LDs.argsort(axis = 1)[:,:SearchRadius]
Values = self.Values[Args.T].T
# A 的逆矩阵
AInv = inv(A)
B = -self.VariogramFUN(LDs, *self.VParametersList)
B[np.abs(LDs) <= self.eps] = 0.0
B = np.pad(B, ((0,0),(0,1)), constant_values = 1)
X = np.dot(B, AInv)
B = B[np.ogrid[:len(B)], Args.T].T
X = X[np.ogrid[:len(X)], Args.T].T
X = X / X.sum(axis = 1, keepdims = True)
UKResults = np.sum(X * Values, axis = 1), np.sum((X * -B), axis = 1)
return UKResults
def _OKExec(self, A, LDs, SearchRadius):
"""普通克里金求解"""
Args = LDs.argsort(axis = 1)[:,:SearchRadius]
LDs = LDs[np.ogrid[:len(LDs)], Args.T].T
B = -self.VariogramFUN(LDs, *self.VParametersList)
B[np.abs(LDs) <= self.eps] = 0.0
B = np.pad(B, ((0,0),(0,1)), constant_values = 1)
OKResults = np.zeros([2, len(LDs)])
for i, b in enumerate(B):
BSelector = Args[i]
ASelector = np.append(BSelector, len(self.AdjustPoints))
a = A[ASelector[:, None], ASelector]
x = solve(a, b)
OKResults[:, i] = x[:SearchRadius].dot(self.Values[BSelector]), -x.dot(b)
return OKResults
def Execute(self, SearchRadius = 12, KMethod = 'Ordinary'):
'''克里金插值'''
initialize.ValueType(SearchRadius, 'pint')
SearchRadius = np.min([SearchRadius, len(self.AdjustPoints)])
A = self._GetKrigingMatrix()
LDs = self.DistanceMethod(self.XYs, self.AdjustPoints)
if KMethod not in ['Universal', 'Ordinary']:
raise ValueError("Undefined Kriging method. Please select 'Universal' or 'Ordinary'!")
elif KMethod == 'Universal':
KResults = self._UKExec(A, LDs, SearchRadius)
else:
KResults = self._OKExec(A, LDs, SearchRadius)
NT = namedtuple('Kriging', ['Data', 'SigmaSQ', 'Transform'])
return NT(KResults[0].reshape(self.YLAT, self.XLON),
KResults[1].reshape(self.YLAT, self.XLON), self.Transform)
三、差值应用
示例数据可从:https://gma.luosgeo.com/ 获取
在 gma 1.0.13.15 之后的版本可以直接引用。这里基于 1.0.13.15之后的版本引用做示例。
import gma
import pandas as pd
Data = pd.read_excel("Interpolate.xlsx")
Points = Data.loc[:, ['经度','纬度']].values
Values = Data.loc[:, ['值']].values
# 普通克里金(球面函数模型)插值
KD = gma.smc.Interpolate.Kriging(Points, Values, Resolution = 0.05,
VariogramModel = 'Spherical',
VariogramParameters = None,
KMethod = 'Ordinary',
InProjection = 'EPSG:4326')
# 泛克里金类似,这里不做示例
gma.rasp.WriteRaster(r'.\gma_OKriging.tif',
KD.Data,
Projection = 'WGS84',
Transform = KD.Transform,
DataType = 'Float32')
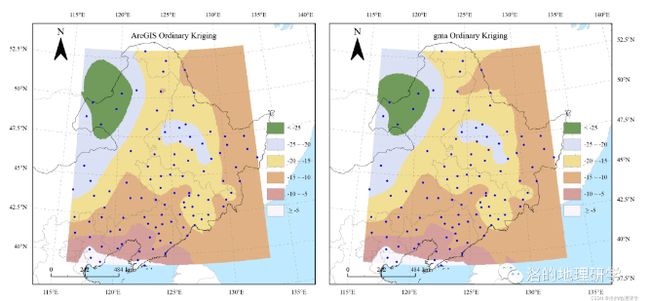
四、结果对比
与 ArcGIS Ordinary Kriging 插值结果(重分类后)对比:
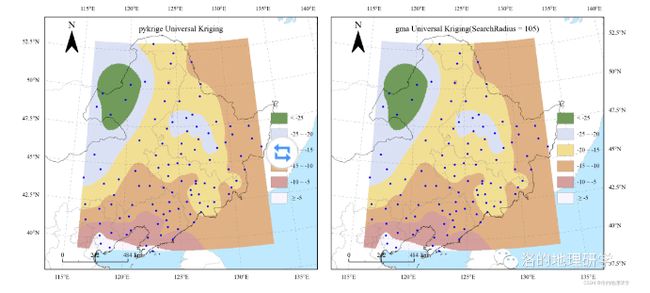
与 pykrige 包 Universal Kriging 插值结果(重分类后)对比:
到此这篇关于Python实现克里金插值法的过程详解的文章就介绍到这了,更多相关Python克里金插值法内容请搜索脚本之家以前的文章或继续浏览下面的相关文章希望大家以后多多支持脚本之家!