洛谷错题笔记

P1042 [NOIP2003 普及组] 乒乓球

题目背景
国际乒联现在主席沙拉拉自从上任以来就立志于推行一系列改革，以推动乒乓球运动在全球的普及。其中 11分制改革引起了很大的争议，有一部分球员因为无法适应新规则只能选择退役。华华就是其中一位，他退役之后走上了乒乓球研究工作，意图弄明白 11 分制和 21 分制对选手的不同影响。在开展他的研究之前，他首先需要对他多年比赛的统计数据进行一些分析，所以需要你的帮忙。

题目描述
华华通过以下方式进行分析，首先将比赛每个球的胜负列成一张表，然后分别计算在 11 分制和 21 分制下，双方的比赛结果（截至记录末尾）。

比如现在有这么一份记录，（其中W 表示华华获得一分，L 表示华华对手获得一分）

WWWWWWWWWWWWWWWWWWWWWWLW

在 1111 分制下，此时比赛的结果是华华第一局 11 比 0 获胜，第二局 11 比 0 获胜，正在进行第三局，当前比分 1 比 1。而在 21 分制下，此时比赛结果是华华第一局 21 比 0 获胜，正在进行第二局，比分 2 比 1。如果一局比赛刚开始，则此时比分为 0 比 0。直到分差大于或者等于 2，才一局结束。

你的程序就是要对于一系列比赛信息的输入（WL 形式），输出正确的结果。

输入格式
每个输入文件包含若干行字符串，字符串有大写的 W 、L 和 E 组成。其中E 表示比赛信息结束，程序应该忽略E 之后的所有内容。

输出格式
输出由两部分组成，每部分有若干行，每一行对应一局比赛的比分（按比赛信息输入顺序）。其中第一部分是 11 分制下的结果，第二部分是 21 分制下的结果，两部分之间由一个空行分隔。

输入 #1

WWWWWWWWWWWWWWWWWWWW
WWLWE
输出 #1

11:0
11:0
1:1

21:0
2:1
说明/提示
每行至多 2525 个字母，最多有 25002500 行。

下面是我的代码：

#include
using namespace std;
const int N = 62510;
string str;
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int m = 0;
    char c;
    while (cin>>c&&c!='E')
    {
        str+=c;
    }
    if(!str[0])
    {
        cout << "0:0"<<endl<<endl<<"0:0";
        return 0;
    } 
    int t1 = 0,t2 = 0;
    int i = 0;
    while (str[i])
    {
        if(str[i]=='W')   t1++;
        else if(str[i]=='L')  t2++;
        i++;
        if((t1>=11||t2>=11)&&fabs(t1-t2)>=2)    
        {
            cout << t1 << ":" << t2 << endl;
            t1 = 0,t2 = 0;
        }
        if(i==str.size()&&(t1!=0||t2!=0))
        {
            cout << t1 << ":" << t2 << endl;
        }
        else if(i==str.size()&&i%11==0)
        {
            cout << t1 << ":" << t2 << endl;
        }

    }
    cout << endl;
    t1 = 0,t2 = 0,i = 0;
    while (str[i])
    {
        if(str[i]=='W')   t1++;
        else if(str[i]=='L')  t2++;
        i++;
        if((t1>=21||t2>=21)&&fabs(t1-t2)>=2)    
        {
            cout << t1 << ":" << t2 << endl;
            t1 = 0,t2 = 0;
        }
        if(i==str.size()&&(t1!=0||t2!=0))
        {
            cout << t1 << ":" << t2 << endl;
        }
        else if(i==str.size()&&i%11==0)
        {
            cout << t1 << ":" << t2 << endl;
        }
    }    
}

这道题起初令我最头疼的是如何按照题意输入数据，之后又理解错了题意，兜兜转转提交了10多次，终于AC了。

心得：

1、这次的输入形式可以作为参考价值，多了解下。

2、用scnaf不好输入但又害怕用cin超时的时候，可以加上那句加速的话，这样就不用怕了！

P1563 [NOIP2016 提高组] 玩具谜题

小南有一套可爱的玩具小人, 它们各有不同的职业。

有一天, 这些玩具小人把小南的眼镜藏了起来。 小南发现玩具小人们围成了一个圈,它们有的面朝圈内,有的面朝圈外。如下图:

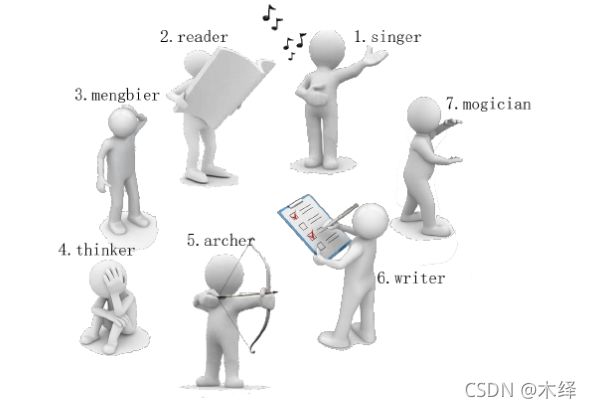
这时singersinger告诉小南一个谜題: “眼镜藏在我左数第3个玩具小人的右数第11个玩具小人的左数第22个玩具小人那里。 ”

小南发现, 这个谜题中玩具小人的朝向非常关键, 因为朝内和朝外的玩具小人的左右方向是相反的: 面朝圈内的玩具小人, 它的左边是顺时针方向, 右边是逆时针方向; 而面向圈外的玩具小人, 它的左边是逆时针方向, 右边是顺时针方向。

小南一边艰难地辨认着玩具小人, 一边数着:

singer朝内, 左数第3个是archer。

archer朝外,右数第1个是thinker。

thinker朝外, 左数第2个是writer。

所以眼镜藏在writerwriter这里!

虽然成功找回了眼镜, 但小南并没有放心。 如果下次有更多的玩具小人藏他的眼镜, 或是谜題的长度更长, 他可能就无法找到眼镜了 。 所以小南希望你写程序帮他解决类似的谜題。 这样的谜題具体可以描述为:

有 n个玩具小人围成一圈, 已知它们的职业和朝向。现在第1个玩具小人告诉小南一个包含m条指令的谜題, 其中第 z条指令形如“左数/右数第s,个玩具小人”。 你需要输出依次数完这些指令后,到达的玩具小人的职业。

输出格式：
输出一个字符串，表示从第一个读入的小人开始，依次数完 m 条指令后到达的小人的职业。
输入 #1
7 3
0 singer
0 reader
0 mengbier
1 thinker
1 archer
0 writer
1 mogician
0 3
1 1
0 2
输出 #1
writer

输入 #2
10 10
1 C
0 r
0 P
1 d
1 e
1 m
1 t
1 y
1 u
0 V
1 7
1 1
1 4
0 5
0 3
0 1
1 6
1 2
0 8
0 4
输出 #2
y

#include
using namespace std;
const int maxn = 1e5+10;
typedef pair<int,int>PII;
vector<PII>v;//可以，靠自己做出来了
struct Person
{
    int num;
    string name;
};
struct Person p[maxn];
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n,m;
    cin >> n >> m;
    for(int i = 1; i <= n; i++)
    {
        cin >> p[i].num >> p[i].name;
    }
    for(int i = 0;i<m;i++)
    {
        int a, b;
        cin >> a >> b;
        v.push_back({a,b});
    }
    int j = 1;
    for(auto i : v)
    {
        if(i.first==0&&p[j].num==0)//顺时针
        {
            if(j-i.second>=1)    j-=i.second;
            else    j += (n-i.second);
        }
        else if(i.first==0&&p[j].num==1) //逆时针
        {
            if(j+i.second<=n)   j+=i.second;
            else    j-=(n-i.second);
        }
        else if(i.first==1&&p[j].num==0)//逆时针
        {
            if(j+i.second<=n)   j+=i.second;
            else    j-=(n-i.second);
        }    
        else if(i.first==1&&p[j].num==1)    //顺时针 
        {
            if(j-i.second>=1)    j-=i.second;
            else    j += (n-i.second);
        } 
    }
    cout << p[j].name;
    return 0;
}

小结：
当时做的时候不知道怎么存储数据，觉得跟应该不属于结构体那一类的知识点了吧，但需要用到的，都得要用上！如果觉得cin，cout更加方便的话，就每次用的时候加上那句加速的话就可以了！

P2089 烤鸡

题目背景
猪猪 Hanke 得到了一只鸡。

题目描述
猪猪 Hanke 特别喜欢吃烤鸡（本是同畜牲，相煎何太急！）Hanke 吃鸡很特别，为什么特别呢？因为他有 10 种配料（芥末、孜然等），每种配料可以放 1 到 3 克，任意烤鸡的美味程度为所有配料质量之和。

现在， Hanke 想要知道，如果给你一个美味程度 n ，请输出这 10 种配料的所有搭配方案。

输入格式
一个正整数 n，表示美味程度。

输出格式
第一行，方案总数。

第二行至结束，10 个数，表示每种配料所放的质量，按字典序排列。

如果没有符合要求的方法，就只要在第一行输出一个 0。
输入输出样例
输入 #1
11
输出 #1
10
1 1 1 1 1 1 1 1 1 2
1 1 1 1 1 1 1 1 2 1
1 1 1 1 1 1 1 2 1 1
1 1 1 1 1 1 2 1 1 1
1 1 1 1 1 2 1 1 1 1
1 1 1 1 2 1 1 1 1 1
1 1 1 2 1 1 1 1 1 1
1 1 2 1 1 1 1 1 1 1
1 2 1 1 1 1 1 1 1 1
2 1 1 1 1 1 1 1 1 1
说明/提示
对于 100% 的数据，n≤5000。

题解：
很显然，极限下就是10个数都为3，即30，我也是万万没有想到暴力法竟然可以解决掉！当时我一直想着next_permutation，觉得有多种情况，实行起来有点复杂。

下面是暴力法代码：

#include
using namespace std;
int a[10];
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    int n;
    cin >> n;
    int sum = 0;
    if(n>30||n<10)//n<10更严谨点
    {
        cout <<"0";
        return 0;
    }
    else
    {
        for(int a = 1;a<=3;a++)
         for(int b = 1;b<=3;b++)
          for(int c = 1;c<=3;c++)
           for(int d = 1;d<=3;d++)
            for(int e = 1;e<=3;e++)
             for(int f = 1;f<=3;f++)
              for(int g = 1;g<=3;g++)
               for(int h = 1;h<=3;h++)
                for(int i = 1;i<=3;i++)
                 for(int j = 1;j<=3;j++)
                  if(a+b+c+d+e+f+g+h+i+j==n) sum++;

        cout << sum << endl;
        for(int a = 1;a<=3;a++)
         for(int b = 1;b<=3;b++)
          for(int c = 1;c<=3;c++)
           for(int d = 1;d<=3;d++)
            for(int e = 1;e<=3;e++)
             for(int f = 1;f<=3;f++)
              for(int g = 1;g<=3;g++)
               for(int h = 1;h<=3;h++)
                for(int i = 1;i<=3;i++)
                 for(int j = 1;j<=3;j++)
                  if(a+b+c+d+e+f+g+h+i+j==n)
                   cout <<a<<" "<<b<<" "<<c<<" "<<d<<" "<<e<<" "<<f<<" "<<g<<" "<<h<<" "<<i<<" "<<j<<endl;
    }
    return 0;
    }

当然了，这道题目有个递归的标签，也可以用DFS处理。

#include
using namespace std;
const int N = 1e6+10;
int cnt,n,a[N][10],temp[11];
void dfs(int step,int sum)//step抽象成第多少步(盒子)
{
    if(step==10)
    {
        if(sum==n)  
        {
            for (int i = 0; i < 10; i++)
            {
                a[cnt][i] = temp[i];
            }
            cnt++;//计数器
        }
        return ;
    }
    for (int i = 1; i <= 3; i++)
    {
        temp[step] = i;
        dfs(step+1,sum+i);
    }
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin >> n;
    dfs(0,0);
    if(!cnt)    cout << '0';
    else
    {
        cout << cnt<< endl;
        for (int i = 0; i < cnt; i++)
        {
            for (int j = 0; j < 10; j++)
            {
                cout << a[i][j] <<" ";
            }
            cout << endl;
        }
    }
    return 0;
}

P3392 涂国旗

题目描述
某国法律规定，只要一个由 N×M 个小方块组成的旗帜符合如下规则，就是合法的国旗。（毛熊：阿嚏——）

从最上方若干行（至少一行）的格子全部是白色的；
接下来若干行（至少一行）的格子全部是蓝色的；
剩下的行（至少一行）全部是红色的；
现有一个棋盘状的布，分成了 N 行 M 列的格子，每个格子是白色蓝色红色之一，小 a 希望把这个布改成该国国旗，方法是在一些格子上涂颜料，盖住之前的颜色。

小a很懒，希望涂最少的格子，使这块布成为一个合法的国旗。
输入格式
第一行是两个整数 N,M。

接下来 N 行是一个矩阵，矩阵的每一个小方块是W（白），B（蓝），R（红）中的一个。
输出格式
一个整数，表示至少需要涂多少块。

输入输出样例

输入 #1
4 5
WRWRW
BWRWB
WRWRW
RWBWR

输出 #1
11

说明/提示
样例解释

目标状态是：
WWWWW
B B B B B
R R R R R
R R R R R
一共需要改 11 个格子。

数据范围
对于 100% 的数据，N,M≤50。

题解：
根据数据的范围，暴力做法可取。
那么主要问题就落在了循环的嵌套上，怎么能遍历各种情况呢？
下面是我的代码：

#include
using namespace std;
const int maxn = 60;
char a[maxn][maxn];//存入数据
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);//加速
    int n,m;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
    {
        for (int j = 1; j <= m; j++)
        {
            cin >> a[i][j];//输入数据
        }
    }
    int ans = 99999999;//先将答案初始化为一个较大的数
    for (int i = 1; i <= n-2; i++)//以W能出现到的最大排数为最外面的循环。
    {
        int res = 0;//循环过程中最小值初始化
        for (int w = 1; w <= i; w++)//从1排W一直到i排个W
        {
            for (int jj = 1; jj <= m; jj++)
            {
                if(a[w][jj]!='W')   res++;
            }
        }
        int temp = res;//暂时记录下将W排排好后的次数
        for (int ii = n-1; ii >= i+1; ii--)//这个循环是一个巧妙之处，是为了处理B排的排数从W的下一排一直到n-1排，下次循环再从W的下一排到n-2排，随着B排的减少，那么R排就要增加，于是就会遍历各种情况。
        {
            for (int j = i+1; j <= ii; j++)//统计B排
            {
                for (int jj = 1; jj <= m; jj++)
                {
                    if(a[j][jj]!='B')   res++;
                }    
            }
            for (int k = ii+1; k <= n; k++)//统计R排
            {
                for (int jj = 1; jj <= m; jj++)
                {
                    if(a[k][jj]!='R')   res++;
                }
            }
            ans = min(ans,res); //刷新最小值
            res =temp;//回到开始排好W排需要的次数，继续遍历其他情况。
        }   
    }
    cout << ans;
    return 0;
}

P2036 [COCI2008-2009#2] PERKET

题目描述
Perket 是一种流行的美食。为了做好 Perket，厨师必须谨慎选择食材，以在保持传统风味的同时尽可能获得最全面的味道。你有 n 种可支配的配料。对于每一种配料，我们知道它们各自的酸度 s 和苦度 b。当我们添加配料时，总的酸度为每一种配料的酸度总乘积；总的苦度为每一种配料的苦度的总和。

众所周知，美食应该做到口感适中，所以我们希望选取配料，以使得酸度和苦度的绝对差最小。

另外，我们必须添加至少一种配料，因为没有任何食物以水为配料的。

输入格式
第一行一个整数 n，表示可供选用的食材种类数。

接下来 n 行，每行 2 个整数 s _i和 b_i，表示第 i 种食材的酸度和苦度。

输出格式
一行一个整数，表示可能的总酸度和总苦度的最小绝对差。

输入输出样例

输入 #1
1
3 10
输出 #1
7

输入 #2
2
3 8
5 8
输出 #2
1

输入 #3
4
1 7
2 6
3 8
4 9
输出 #3
1
说明/提示
数据规模与约定
对于 100% 的数据，有 1≤n≤10，且将所有可用食材全部使用产生的总酸度和总苦度小于1×10^9，酸度和苦度不同时为 1 和 0。
题解：
如何能将各种情况都遍历到呢？天秀的dfs两行代码无可比拟。

#include
using namespace std;
int res = INT_MAX;
int x[15],y[15];//x表示酸度，y表示苦度
int n;
void dfs(int num,int s,int b)//s表示总酸度,b表示总苦度
{
    if(num>n)
    {
        if(s==1&&b==0)  return;
        res = min(res,abs(s-b));//abs()是求绝对值的!
        return;
    }
    dfs(num+1,s*x[num],b+y[num]);//天秀的两行递归代码
    dfs(num+1,s,b);
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
    cin >> n;
    for(int i = 1;i <= n;i++)   cin >> x[i] >> y[i];
    dfs(1,1,0);
    cout << res;
    return 0;
}

P1157 组合的输出

题目描述
排列与组合是常用的数学方法，其中组合就是从n个元素中抽出r个元素(不分顺序且r≤n)，我们可以简单地将n个元素理解为自然数1,2,…,n，从中任取r个数。

现要求你输出所有组合。

例如n=5,r=3，所有组合为：

123,124,125,134,135,145,234,235,245,345

输入格式
一行两个自然数n,r(1 输出格式
所有的组合，每一个组合占一行且其中的元素按由小到大的顺序排列，每个元素占三个字符的位置，所有的组合也按字典顺序。
**注意哦!输出时，每个数字需要3个场宽，pascal可以这样：

write(ans:3);
输入输出样例

输入 #1
5
3
输出 #1
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5
下面是DFS代码：

#include
using namespace std;
int n,r;
const int N = 1e4;
int a[N];
void dfs(int step,int x)
{
    if(step==r+1)
    {
        for (int i = 1; i <= r; i++)
        {
            printf("%3d",a[i]);
        }
        printf("\n");
        return ;
        }
    for (int i = x+1; i <= n; i++)//这个i非常秀，就避免了前一个数大于后一个数的情况。
    {
        a[step] = i;
        dfs(step+1,i);
    }
    return ;
}
int main()
{
    scanf("%d%d",&n,&r);
    dfs(1,0);
    return 0;
}

P1372 又是毕业季I

[题目链接]又是毕业季I - 洛谷

题目背景
“叮铃铃铃”，随着高考最后一科结考铃声的敲响，三年青春时光顿时凝固于此刻。毕业的欣喜怎敌那离别的不舍，憧憬着未来仍毋忘逝去的歌。1000 多个日夜的欢笑和泪水，全凝聚在毕业晚会上，相信，这一定是一生最难忘的时刻！

题目描述
为了把毕业晚会办得更好，老师想要挑出默契程度最大的 kk 个人参与毕业晚会彩排。可是如何挑呢？老师列出全班同学的号数 1,2,…,n 并且相信 k 个人的默契程度便是他们的最大公约数（这不是迷信哦~）。这可难为了他，请你帮帮忙吧！

PS：一个数的最大公约数即本身。

输入格式
两个空格分开的正整数 n 和 k。

输出格式
一个整数，为最大的默契值。

输入输出样例
输入 #1

4 2

输出 #1

2

说明/提示
对于 20% 的数据，k≤2，n≤10^3。

对于另 30% 的数据，k≤10，n≤100。

对于 100% 的数据，k≤10^9，n≤109，n≥k≥1（神犇学校，人数众多）。

下面是我的代码：

#include
using namespace std;
int main()
{
    int n,k;
    scanf("%d%d",&n,&k);
    printf("%d",n/k);
    return 0;
}

分析：这道题刚开始以为是求所给两个数的最大公约数，之后看了多篇文章才渐渐理解了题意。

知识点：

对于两个数：如果两个数成倍数关系时，它们的最大公因数是两数中的较小数，则这个较小数为这两个数的最大公约数。

题解：

那么对于题目所给的k个数，X1，X2，…Xk这k个数则满足：x1max_gcd(X1 = x1max_gcd)、x2max_gcd…xkmax_gcd。则最大的数xkmax_gcd<=n。即最大的数要小于等于总人数。故需满足公式：kmax_gcd <= n。

因此本题的答案就是：n/k(向下取整).

​