算法学习:一、排序算法
参考:https://blog.csdn.net/weixin_37818081/article/details/79202115
https://blog.csdn.net/qq_28081081/article/details/80598960
https://www.cnblogs.com/chengxiao/p/6194356.html
https://www.cnblogs.com/9dragon/p/10739121.html
排序就是将一组对象
less方式是对元素进行比较,exch()方法是对元素交换位置
一、选择排序
一种最简单的排序算法是这样的,首先找到数组中最小的元素,然后将它和数组的第一个元素交换位置(如果第一个元素就是最小元素那么它就和自己交换)。再次,在剩下的元素中找到最小的元素,将它和数组的第二个元素交换位置。如此往复,直到将整个数组排序。这种就是选择排序,因为它在不断地选择剩余元素之中的最小者。
Java实现
public class Selection{
public static void sort(Comparable[] a){
//将a[]按升序排序
int N=a.length;
for(int i=0;iPython实现
def selectSort(list):
for i in range(len(list)-1):
min=i
for j in range(i,len(list)):
if list[j]Go语言实现
func Select(num []int64) []int64{
for i:=0;inum[j]{
min=num[j]
local=j
}
}
Swap(num,local,i)
}
return num
}
func Swap(num []int64,i int,j int){
temp :=num[i]
num[i]=num[j]
num[j]=temp
}
Scala版
object SelectionSort extends Utils with App{
def sort(unSorted : Array[Int]) : Array[Int]={
for(i<-0 until unSorted.size){
var min=unSorted(i)
var minIndex=i
for(j<-i+1 until unSorted.size){
if(unSorted(j)<=min){
min=unSorted(j)
minIndex=j
}
}
if(minIndex!=i){
swap(unSorted,i,minIndex)
}
}
unSorted
}
val list=Array(14,52,21,3)
printlnArray(list.sorted)
printlnArray(sort(list))
}总的来说,选择排序是一种很容易理解和实现的简单排序算法,它有两个很鲜明的特点。
1、运行时间和输入无关。为了找出最小的元素而扫描一遍数组并不能为下一遍扫描提供什么信息,这种性质在某些情况下是缺点,因为使用选择排序的人可能会发现,一个已经有序的数组或是主键全部相等的数组和一个元素随机排列的数组所用的排序时间竟然是一样长的,我们将会看到,其他算法会更善于利用输入的初始状态。
2、数据移动是最少的。每次交换都会改变两个数组元素的值,因此选择排序用了N次交换——交换次数和数组的大小都是线性关系。
二、插入排序
通常人们整理桥牌的方法是一张一张的来,将每一张牌插入到其他已经有序的牌中的适当位置。在计算机的实现中,为了给要插入的元素腾出空间,我们需要将其余所有元素在插入之前都向右移动一位,这种算法叫做插入排序。。
与选择排序一样,当前索引左边的所有元素都是有序的,但他们的最终位置还不确定,为了给更小的元素腾出空间,他们可能会被移动。但是当索引到达数组的右端,数组排序就完成了。
和选择排序不同的是,插入排序所需时间取决于输入中元素的初始顺序。例如,对一个很大且其中的元素已经有序(或接近有序)的数组进行排序将会比对随机顺序的数组或是逆序数组进行排序要快的多。
Java实现
public class Insertion{
public static void sort(Comparable[] a){
//将a[]按升序排序
int N=a.length;
for(int i=1;i0&&less(a[j],a[j-1]);j--){
exch(a,j,j-1);
}
}
}
} Python实现
def insertSort(list)
for i in range(1,len(list)):
j=i-1
key=list[i]
while j>=0:
if list[j]>key:
list[j+1]=list[j]
list[j]=key
j -=1
return list
print(insertSort([1,3,2]))Go语言实现
func insertSort(nums []int){
for i:=1;i=0&&nums[j]>temp{
nums[j+1]=nums[j]
j--
}
nums[j+1]=temp
}
}
} Scala语言实现
def SinsrtSort(inputData:ArrayBuffer[Int]):ArrayBuffer[Int]={
for(i<-1 until inputData.length){
val x=inputData(i)
var j=i-1
while(j>0&&x要大幅度提高插入排序的速度也不难,只需要在内循环中将较大的元素都向右移动而不总是交换两个元素。
总的来说,插入排序对于部分有序的数组十分高效,也很适合小规模数组。
三、希尔排序
希尔排序举例:
1>下面给出一个数据列:
![]()
2>第一趟取increment的方法是:n/3向下取整+1=3(关于increment的取法之后会有介绍)。将整个数据列划分为间隔为3的3个子序列,然后对每一个子序列执行直接插入排序,相当于对整个序列执行了部分排序调整。图解如下:
![]()
3>第二趟将间隔increment= increment/3向下取整+1=2,将整个元素序列划分为2个间隔为2的子序列,分别进行排序。图解如下:
![]()
4>第3趟把间隔缩小为increment= increment/3向下取整+1=1,当增量为1的时候,实际上就是把整个数列作为一个子序列进行插入排序,图解如下:
![]()
5>直到increment=1时,就是对整个数列做最后一次调整,因为前面的序列调整已经使得整个序列部分有序,所以最后一次调整也变得十分轻松,这也是希尔排序性能优越的体现。
Java实现
public void shell(){
int[] ins={4,3,1,2};
int n = ins.length;
int gap = n/2;
while(gap > 0){
for(int j = gap; j < n; j++){
int i=j;
while(i >= gap && ins[i-gap] > ins[i]){
int temp = ins[i-gap]+ins[i];
ins[i-gap] = temp-ins[i-gap];
ins[i] = temp-ins[i-gap];
i -= gap;
}
}
gap = gap/2;
}
}四、快速排序
快速排序流行的原因是它实现简单,适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。快速排序引人注目的特点包括它是原地排序(只需要一个很小的辅助栈),且将长度为N的数组排序所需的时间和NlgN成正比。快速排序的内循环比大多数排序算法都要短小,这意味着它无论是在理论上还是实际中都要更快。它的主要缺点是非常脆弱,在实现时要非常小心才能避免低劣的性能。
快速排序是一种分治的排序算法。它将一个数组分成两个子数组,将两部分独立地排序。快速排序和归并排序是互补的:归并排序将数组分成两个子数组分别排序,,并将有序的子数组归并以将整个数组排序;而快速排序将数组排序的方法则是当两个子数组都有序时整个数组也就自然有序了。在第一种情况中,递归调用发生在处理整个数组之前;第二种情况,递归调用发生在处理整个数组之后。在归并排序中,一个数组被等分为两半;在快速排序中,切分的位置取决于数组的内容。
Java实现
public int getMiddle(int[] numbers, int low,int high)
{
int temp = numbers[low]; //数组的第一个作为中轴
while(low < high)
{
while(low < high && numbers[high] > temp)
{
high--;
}
numbers[low] = numbers[high];//比中轴小的记录移到低端
while(low < high && numbers[low] < temp)
{
low++;
}
numbers[high] = numbers[low] ; //比中轴大的记录移到高端
}
numbers[low] = temp ; //中轴记录到尾
return low ; // 返回中轴的位置
}
public void quickSort(int[] numbers,int low,int high)
{
if(low < high)
{
int middle = getMiddle(numbers,low,high); //将numbers数组进行一分为二
quickSort(numbers, low, middle-1); //对低字段表进行递归排序
quickSort(numbers, middle+1, high); //对高字段表进行递归排序
}
}五、归并排序
归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
分而治之
![]()
可以看到这种结构很像一棵完全二叉树,本文的归并排序我们采用递归去实现(也可采用迭代的方式去实现)。分阶段可以理解为就是递归拆分子序列的过程,递归深度为log2n。
合并相邻有序子序列
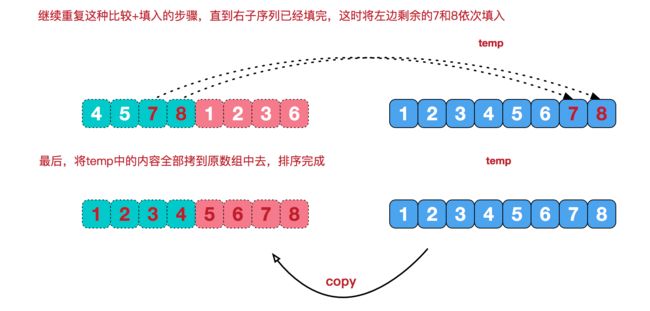
再来看看治阶段,我们需要将两个已经有序的子序列合并成一个有序序列,比如上图中的最后一次合并,要将[4,5,7,8]和[1,2,3,6]两个已经有序的子序列,合并为最终序列[1,2,3,4,5,6,7,8],来看下实现步骤。
归并排序是稳定排序,它也是一种十分高效的排序,能利用完全二叉树特性的排序一般性能都不会太差。java中Arrays.sort()采用了一种名为TimSort的排序算法,就是归并排序的优化版本。从上文的图中可看出,每次合并操作的平均时间复杂度为O(n),而完全二叉树的深度为|log2n|。总的平均时间复杂度为O(nlogn)。而且,归并排序的最好,最坏,平均时间复杂度均为O(nlogn)。
Java实现
public void sort(int[] arr) {
int[] temp = new int[arr.length];//在排序之前,先建好一个长度等于原数组长度的临时数组,避免递归中频繁开辟空间
sort(arr, 0, arr.length - 1, temp);
}
public void sort(int[] arr, int left, int right, int[] temp) {
if (left < right) {
int mid = (left + right) / 2;
sort(arr, left, mid, temp);//左边归并排序,使得左子序列有序
sort(arr, mid + 1, right, temp);//右边归并排序,使得右子序列有序
merge(arr, left, mid, right, temp);//将两个有序子数组合并操作
}
}
public void merge(int[] arr, int left, int mid, int right, int[] temp) {
int i = left;//左序列指针
int j = mid + 1;//右序列指针
int t = 0;//临时数组指针
while (i <= mid && j <= right) {
if (arr[i] <= arr[j]) {
temp[t++] = arr[i++];
} else {
temp[t++] = arr[j++];
}
}
while (i <= mid) {//将左边剩余元素填充进temp中
temp[t++] = arr[i++];
}
while (j <= right) {
temp[t++] = arr[j++];
}
t = 0;
//将temp中元素全部拷贝到原数组中
while (left <= right) {
arr[left++] = temp[t++];
}
}六、优先队列
A、队列与优先队列的区别
- 队列是一种FIFO(First-In-First-Out)先进先出的数据结构,对应于生活中的排队的场景,排在前面的人总是先通过,依次进行。
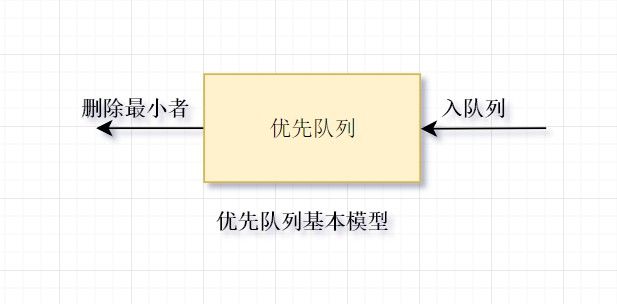
- 优先队列是特殊的队列,从“优先”一词,可看出有“插队现象”。比如在火车站排队进站时,就会有些比较急的人来插队,他们就在前面先通过验票。优先队列至少含有两种操作的数据结构:insert(插入),即将元素插入到优先队列中(入队);以及deleteMin(删除最小者),它的作用是找出、删除优先队列中的最小的元素(出队)。
优先队列
B、优先队列(堆)的特性
-
优先队列的实现常选用二叉堆,在数据结构中,优先队列一般也是指堆。
-
堆的两个性质:
-
结构性:堆是一颗除底层外被完全填满的二叉树,底层的节点从左到右填入,这样的树叫做完全二叉树。
-
堆序性:由于我们想很快找出最小元,则最小元应该在根上,任意节点都小于它的后裔,这就是小顶堆(Min-Heap);如果是查找最大元,则最大元应该在根上,任意节点都要大于它的后裔,这就是大顶堆(Max-heap)。
结构性:
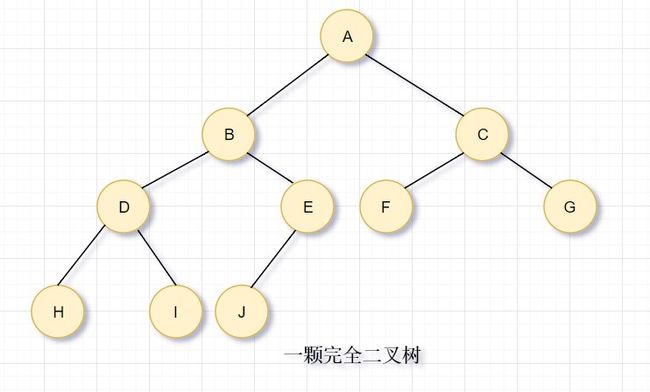
完成二叉树
通过观察发现,完全二叉树可以直接使用一个数组表示而不需要使用其他数据结构。所以我们只需要传入一个size就可以构建优先队列的结构(元素之间使用compareTo方法进行比较)。
public class PriorityQueue> {
public PriorityQueue(int capacity) {
currentSize = 0;
array = (T[]) new Comparable[capacity + 1];
}
}
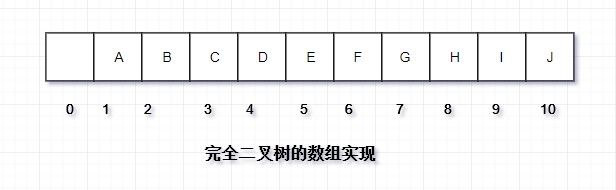
完全二叉树的数组实现
对于数组中的任意位置 i 的元素,其左儿子在位置 2i 上,则右儿子在 2i+1 上,父节点在 在 i/2(向下取整)上。通常从数组下标1开始存储,这样的好处在于很方便找到左右、及父节点。如果从0开始,左儿子在2i+1,右儿子在2i+2,父节点在(i-1)/2(向下取整)。
堆序性:
我们这建立最小堆,即对于每一个元素X,X的父亲中的关键字小于(或等于)X中的关键字,根节点除外(它没有父节点)。
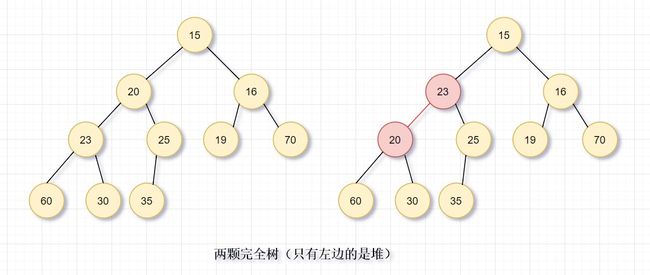
堆
如图所示,只有左边是堆,右边红色节点违反堆序性。根据堆序性,只需要常O(1)找到最小元。
C、基本的堆操作
- insert(插入)
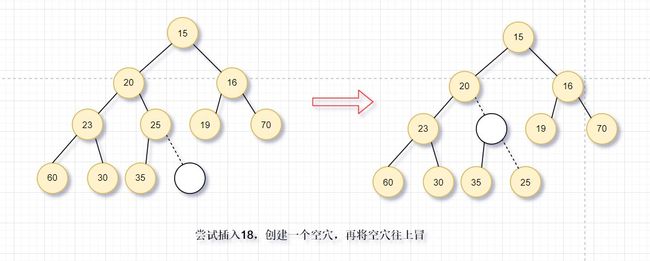
- 上滤:为了插入元素X,我们在下一个可用的位置建立空穴(否则会破坏结构性,不是完全二叉树)。如果此元素放入空穴不破坏堆序性,则插入完成;否则,将父节点下移到空穴,即空穴向根的方向上冒一步。继续该过程,直到X插入空穴为止。这样的过程称为上滤。
建立空穴
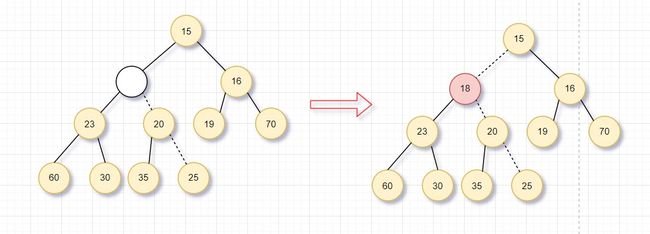
完成插入
图中演示了18插入的过程,在下一个可用的位置建立空穴(满足结构性),发现不能直接插入,将父节点移下来,空穴上冒。继续这个过程,直到满足堆序性。这样就实现了元素插入到优先队列(堆)中。
- java实现上滤
/**
* 插入到优先队列,维护堆序性
*
* @param x :插入的元素
*/
public void insert(T x) {
if (null == x) {
return;
}
//扩容
if (currentSize == array.length - 1) {
enlargeArray(array.length * 2 + 1);
}
//上滤
int hole = ++currentSize;
for (array[0] = x; x.compareTo(array[hole / 2]) < 0; hole /= 2) {
array[hole] = array[hole / 2];
}
array[hole] = x;
}
/**
* 扩容方法
*
* @param newSize :扩容后的容量,为原来的2倍+1
*/
private void enlargeArray(int newSize) {
T[] old = array;
array = (T[]) new Comparable[newSize];
System.arraycopy(old, 0, array, 0, old.length);
}
可以反复使用交换操作来进行上滤过程,但如果插入X上滤d层,则需要3d次赋值;我们这种方式只需要d+1次赋值。
如果插入的元素是新的最小元从而一直上滤到根处,那么这种插入的时间长达O(logN)。但平均来看,上滤终止得要早。业已证明,执行依次插入平均需要2.607次比较,因此平均insert操作上移元素1.607层。上滤次数只比插入次数少一次。
- deleteMin(删除最小元)
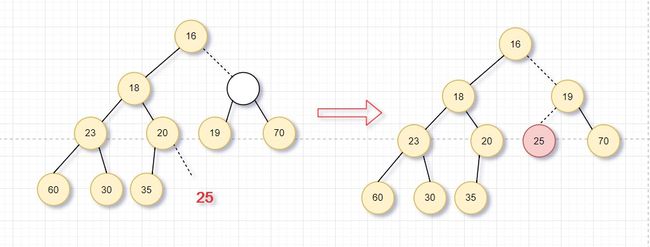
- 下滤:类似于上滤操作。因为我们建立的是最小堆,所以删除最小元,就是将根节点删掉,这样就破坏了结构性。所以我们在根节点处建立空穴,为了满足结构性,堆中最后一个元素X必须移动到合适的位置,如果可以直接放到空穴,则删除完成(一般不可能);否则,将空穴的左右儿子中较小者移到空穴,即空穴下移了一层。继续这样的操作,直到X可以放入到空穴中。这样就可以满足结构性与堆序性。这个过程称为下滤。
删除最小元
完成删除最小元
如图所示:在根处建立空穴,将最后一个元素放到空穴,已满足结构性;为满足堆序性,需要将空穴下移到合适的位置。
注意:堆的实现中,经常发生的错误是只有偶数个元素,即有一个节点只有一个儿子。所以需要测试右儿子的存在性。
/**
* 删除最小元
* 若优先队列为空,抛出UnderflowException
*
* @return :返回最小元
*/
public T deleteMin() {
if (isEmpty()) {
throw new UnderflowException();
}
T minItem = findMin();
array[1] = array[currentSize--];
percolateDown(1);
return minItem;
}
/**
* 下滤方法
*
* @param hole :从数组下标hole1开始下滤
*/
private void percolateDown(int hole) {
int child;
T tmp = array[hole];
for (; hole * 2 <= currentSize; hole = child) {
//左儿子
child = hole * 2;
//判断右儿子是否存在
if (child != currentSize &&
array[child + 1].compareTo(array[child]) < 0) {
child++;
}
if (array[child].compareTo(tmp) < 0) {
array[hole] = array[child];
} else {
break;
}
}
array[hole] = tmp;
}
这种操作最坏时间复杂度是O(logN)。平均而言,被放到根处的元素几乎下滤到底层(即来自的那层),所以平均时间复杂度是O(logN)。
D、总结
优先队列常使用二叉堆实现,本篇图解了二叉堆最基本的两个操作:插入及删除最小元。insert以O(1)常数时间执行,deleteMin以O(logN)执行。相信大家看了之后就可以去看java的PriorityQueue源码了。今天只说了二叉堆最基本的操作,还有一些额外操作及分析下次再说。比如,如何证明buildHeap是线性的?以及优先队列的应用等。
七、冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
/**
* 冒泡排序
* 比较相邻的元素。如果第一个比第二个大,就交换他们两个。
* 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对。在这一点,最后的元素应该会是最大的数。
* 针对所有的元素重复以上的步骤,除了最后一个。
* 持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。
* @param numbers 需要排序的整型数组
*/
public static void bubbleSort(int[] numbers)
{
int temp = 0;
int size = numbers.length;
for(int i = 0 ; i < size-1; i ++)
{
for(int j = 0 ;j < size-1-i ; j++)
{
if(numbers[j] > numbers[j+1]) //交换两数位置
{
temp = numbers[j];
numbers[j] = numbers[j+1];
numbers[j+1] = temp;
}
}
}
}