动态规划入门
前言:首先,什么是动态规划?
动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优值的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题,然后从这些子问题的解得到原问题的解。与分治法不同的是,适合于用动态规划求解的问题,经分解得到子问题往往不是互相独立的。
我们都熟知的斐波那切数列问题就是典型的动态规划问题,后面的问题的解,与前面已经求出来的问题的解有关,也就是我们经常在递归中用公式 f[i]=f[i-1]+f[i-2](i>2),在动态规划中,我们也把这种类型的公式叫做状态转移方程。
我们的动态规划算法,本质上是由dfs而来,经历了dfs->记忆化搜索->动态规划的过程,可以说,动态规划就是dfs的提高。
1.典例引入:
爬楼梯(斐波那切数列的应用)
这就是典型的斐波那切数列问题,我们跳到第i级台阶有两种可行方案,第一种是从第i-1级台阶上跳一步,另一种是从第i-2级台阶跳两步,而第i-1级台阶和第i-2级台阶也分别可以由两种不同的方案,当然我们需要知道前两个初始值,以便让我们开始循环求解方案数,而我们易知第一级台阶只有一种方案,第二节台阶有两种方案,从第三极台阶开始我们就可以通过递归来求解了,当然,这个例子想必自然不用多说,但凡学过递归的,肯定都是老生常谈的例子了,这里直接给出代码,给后续的例题提供模板。
#include
using namespace std;
const int maxn = 20;
int n;
int dfs(int n)
{
if (n == 1)
return 1;
else if (n == 2)
return 2;
else
return dfs(n - 1) + dfs(n - 2);
}
int main()
{
cin >> n;
cout << dfs(n) << endl;
return 0;
} 1.1从dfs到记忆化搜索再到动态规划的优化算法
上面的斐波那切数列数列式的问题,在数据不大的前提下我们的dfs是可行的,但是,我们知道dfs的执行过程实际上是极为复杂的,这中间多次重复的调用已经求出的值,我们可以进一步优化算法,把子问题的答案存起来,去掉重复值;
1.1.1 记忆化搜索
所谓记忆化搜索,就是将已经求出的子问题的答案保存在数组中,当我们在求解一个问题是,先查找数组中是否已有答案,查到直接返回数组值,没查到再进行递归求解,这样可以省去重复的分支,优化时间复杂度。(这里不考虑数据溢出的问题,事实上,当我们的n为50的时候就已经爆int了~~)
#include
using namespace std;
const int maxn = 1005;
int n;
int mem[maxn];
int dfs(int n)
{
if (mem[n])
return mem[n];
int sum = 0;
if (n == 1)
sum = 1;
else if (n == 2)
sum = 2;
else
sum = dfs(n - 1) + dfs(n - 2);
mem[n] = sum;
return sum;
}
int main()
{
cin >> n;
memset(mem, 0, sizeof(mem));
cout << dfs(n) << endl;
return 0;
} 1.1.2 动态规划
我们的动态规划实际上就是记忆化搜索的改进,本质上还是递归,递(把一个大问题分解成一个个子问题,相当于自顶向下求解)归(由最小子问题答案带回求出大问题答案,相当于自底向上返回大问题答案),动态规划,就是省去“递”的过程,直接从已知子问题开始,逐步求解大问题,直到求出大问题的解。
#include
using namespace std;
const int maxn = 1005;
int n;
int f[maxn];
//sum = dfs(n - 1) + dfs(n - 2);
int main()
{
cin >> n;
f[1] = 1;
f[2] = 2;
if(n==1||n==2)
{
cout< *1.1.3三变量的再优化(空间复杂度的优化)
在上述的递推过程中我们不难发现,f[i]的取值只和f[i-1]还有f][i-2]有关,我们可以直接用三个变量来代替整个数组来优化空间,这个并不难能想到,这里只是一提,事实上,在一些竞赛等方面,时间复杂的才是更重要的考察点。
#include
using namespace std;
const int maxn = 1005;
int n;
int ans = 0;
int main()
{
cin >> n;
if (n == 1 || n == 2)
{
cout << n << endl;
return 0;
}
int f1 = 1, f2 = 2;
for (int i = 3; i <= n; i++)
{
ans = f1 + f2;
f1 = f2;
f2 = ans;
}
cout << ans << endl;
return 0;
} 2.渐入佳境
相信你可能已经跃跃欲试了,这不就来了嘛
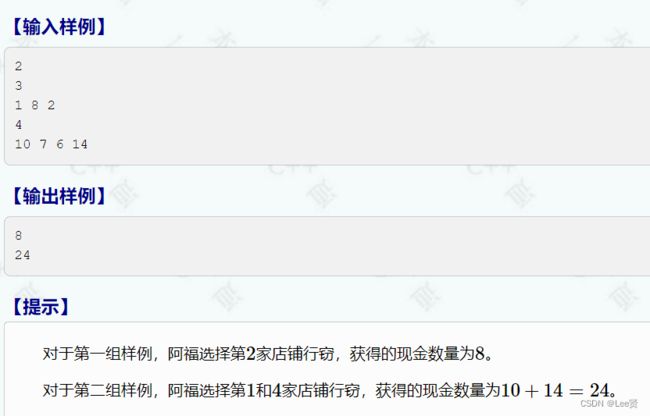
这个题可能刚开始并不容易想到思路,因为这并不像前面的爬楼梯一样是简单的方案数相加问题了,这是一道求最优解的问题,我们来捋下思路,
那我,我们现在就可以很容易的写出dfs版的代码:
#include
using namespace std;
const int maxn = 1e5 + 5;
int T,n;
int ans = 0;
int w[maxn];//表示店铺的价值
int dfs(int x)//x表示第x家店铺
{
if (x > n)
return 0;
else
return max(dfs(x + 1), dfs(x+2) + w[x]);//x+1表示第x家店铺不选,那么这家店铺的价值就肯定得不到了,x+2表示选择第x+2加店铺,说明选择了第x家店铺
}
int main()
{
cin >> T;
while (T--)
{
cin >> n;
for (int i = 1; i <= n; i++)
cin >> w[i];
int ret=dfs(1);
cout << ret << endl;
}
return 0;
} 上面的代码很存在很多的重复性的子分支存在,很遗憾的,这段代码会TLE的,那我在我们之前的优化中,就要采用记忆化搜索和动态规划来优化时间了,
2.1.记忆化搜索改进
#include
using namespace std;
const int maxn = 1e5 + 5;
int T,n;
int ans = 0;
int w[maxn];//表示店铺的价值
int mem[maxn];
int dfs(int x)//x表示第x家店铺
{
if (mem[x])
return mem[x];
int sum = 0;
if (x > n)
sum = 0;
else
sum= max(dfs(x + 1), dfs(x+2) + w[x]);//x+1表示第x家店铺不选,那么这家店铺的价值就肯定得不到了,x+2表示选择第x+2加店铺,说明选择了第x家店铺
mem[x] = sum;
return sum;
}
int main()
{
cin >> T;
while (T--)
{
memset(mem, 0, sizeof(mem));
cin >> n;
for (int i = 1; i <= n; i++)
cin >> w[i];
int ret=dfs(1);
cout << ret << endl;
}
return 0;
} 2.2动态递归
我们在一般的竞赛中,记忆化数组还是不常用的,事实上,上一个题的记忆化搜索已经可以AC了,我们还是来搞一下比较常用的动态规划
#include
using namespace std;
const int maxn = 1e5 + 5;
int T,n;
int w[maxn];//表示店铺的价值
int f[maxn];
//max(dfs(x + 1), dfs(x+2) + w[x]);//x+1表示第x家店铺不选,那么这家店铺的价值就肯定得不到了,x+2表示选择第x+2加店铺,说明选择了第x家店铺
int main()
{
cin >> T;
while (T--)
{
memset(f, 0, sizeof(f));
cin >> n;
for (int i = 1; i <= n; i++)
cin >> w[i];
for (int i = n; i >= 1; i--)
{
f[i] = max(f[i+1], f[i + 2] + w[i]);//由底层求到根节点
}
cout << f[1] << endl;
}
return 0;
} 很多人可能不理解为什么要逆序来进行递推,说实话,一开始我也不太理解,但是我们来看,在上面的二叉树类型的结构中,我们需要根据上面所求得的答案来推出下面的最优解,也就是相当于最小的已知子问题是我先把第一个元素作为条件开始进行递归的,第一个子问题的答案我们是知道的,动态规划的本质就是从大的未知问题向小的已知的子问题的“归”操作,并且我们的递归过程一定是从大问题到小问题的“回溯”过程中才能得出答案的,假如我们用的是正序,那么状态转移方程就要变变形式了。
#include
using namespace std;
const int maxn = 1e5 + 5;
int T,n;
int w[maxn];//表示店铺的价值
int f[maxn];
//max(dfs(x + 1), dfs(x+2) + w[x]);//x+1表示第x家店铺不选,那么这家店铺的价值就肯定得不到了,x+2表示选择第x+2加店铺,说明选择了第x家店铺
int main()
{
cin >> T;
while (T--)
{
memset(f, 0, sizeof(f));
cin >> n;
for (int i = 1; i <= n; i++)
cin >> w[i];
//for (int i = n; i >= 1; i--)
//{
// f[i] = max(f[i+1], f[i + 2] + w[i]);//由底层求到根节点
//}
//cout << f[1] << endl;
for (int i = 1; i <= n; i++)
{
//f[i] = max(f[i - 1], f[i - 2] + w[i]);//因为i为1时数组会越界,所以我们同时让下标加2
f[i+2] = max(f[i+1], f[i] + w[i]);//由根节点求到叶子结点
}
cout << f[n+2] << endl;
}
return 0;
} 可见两种形式的状态转移方程虽然不相同,但是两者的本质都是通过大问题像小问题递归进行的求解。
3.典例1
题目并不难理解(看好了哈,这个不是那个有向左走次数与向右走次数的差不超过1的那个),他是想让我们找出来一条最长路径,结合我们的前面的讲解,我们不难给出下面的dfs代码:
#include
using namespace std;
const int maxn = 105;
int n;
int mp[maxn][maxn];//表示店铺的价值
int dfs(int x, int y)
{
if (x > n||y>n)
return 0;
else
return max(dfs(x+1,y),dfs(x+1,y+1)) + mp[x][y];
}
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
cin >> mp[i][j];
cout << dfs(1, 1) << endl;
return 0;
} 看看数据量,1000行,dfs肯定会崩掉的,我们只能来优化,
记忆化搜索的方法我这里就不展开写了,毕竟模板在那挺好写的,我们直接来看重头戏动态规划
3.1动态规划法降低时间复杂度
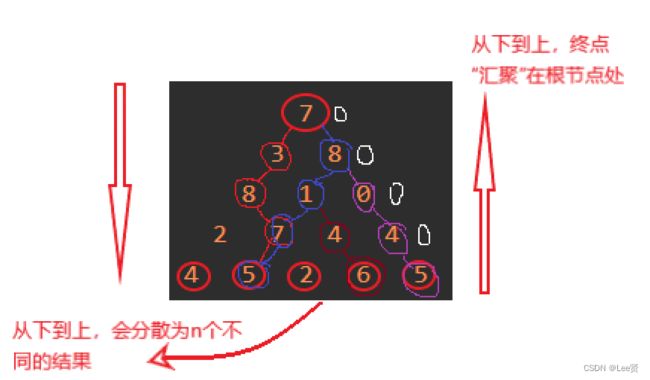
我们先来画出递归树:
从以上来看,我们的递推方程也会有正推和逆推两种方式,这两种方式的不同之处在于:
对于正推(也就是从上往下推)
我们现在已知的子问题是最上层的7这个点,因为它只有一个选择,我们需要每次为该层的子问题选择最优解,我们知道从上往下看,要求是选右下或者正下(在二维数组中是这样的,在该图中就是左下),那么相当于我们在二维数组中,我们向最大层靠近(向下层)的过程中,就要每次选择上层的正上方的数或者左上方的数,然后取他们的最大值即可,当我们取到最后一行时,因为我们是for循环遍历,所以每个数都会遍历到,也就造成了我们的第n行每一列都会有一个最大值,我们无法确定最后一行哪一列才是最大值,所以最后还需要求出最大的那个数。
对于逆推
逆推则是从第n行出发,我们每次寻找的是使我们当前这一层能取到最,我们的最终结果应该汇聚到最顶部的根节点上,所以我们应该把每层的结果放到上一层中去,逐层往上送至顶点处,所以我们对于每个点的选择应该还是遵从选择右下或者正下的,也就是说,我们应该使起点处为该节点所对应的值(比如最后一行的第一个节点对应的值应该为4),所以虽然是向上遍历,但是我们的选择还是来自下方的两个数,这样既保证了我们第n行的n个起点的值为节点值,也保证了我们选择最大值得目的。
这是代码:
#include
using namespace std;
const int maxn = 105;
int n;
int mp[maxn][maxn];//表示店铺的价值
int f[maxn][maxn];
int main()
{
cin >> n;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= i; j++)
cin >> mp[i][j];
//正推
for(int i=1;i<=n;i++)
for (int j = 1; j <= i; j++)
{
f[i][j] = max(f[i -1][j], f[i - 1][j - 1]) + mp[i][j];
}
//这里我们需要注意的是,我们一次所求出的f[i][j]只是相对的第n行其中一个位置的加和最大值,也就是说我们在这次循环结束后并不能马上求出最大值,我们的最大值在第n行中,但是我们不能确定在第几列,所以我们要排序寻找
sort(f[n]+1, f[n] + n+1);
cout << f[n] << endl;
//逆推
//for (int i = n; i >= 1; i--)
// for (int j = 1; j <= i; j++)
// f[i][j] = max(f[i + 1][j], f[i + 1][j + 1]) + mp[i][j];
我们的终点只有一个,所以说递推的终点只有一个
//cout << f[1][1] << endl;
return 0;
} 间章规律小总结(不知对否,还请慎读)
从上面的例子中我们不难的发现,动态规划本质上就是递归加递推的过程,一边递归一遍利用递推公式求解上层问题,其中递归的过程体现在for循环中,递推的过程体现在状态转移方程中,还记得我开头提过的动态规划在“归”的过程中出结果吗,准确的来说是在递推的过程中出结果,我们都知道“递”和“归”是两个相反的过程,同样的,递归和递推也是如此,细心地朋友可能会发现,在上面的两种正逆序的不同遍历过程中,实际上他们所对应的递推公式也是相反的,直白的说,for循环和状态转移方程是相反的,在我们上面的典例1中,for循环由上向下遍历,那么状态转移方程的每一个状态就和前一个状态有关,反之,如果是逆序遍历,相当于递归方向由下到上,那么递推就要与其相反才能有效的求出结果从而退出递归状态,因而每个点的状态由他的后一个状态求出,(如果我嘟囔错了,还请给位大佬帮忙指正~~多谢)。
By the way:前面的f表示的二维数组其实可以直接优化成一维数组,我们只需要保留上一层的对应的状态即可(别试正推,因为不行~QAQ)
但是这个要慎用,一般不推荐,搞不好正逆推会出错的,写这个只是为了知道一些大佬写题解会用一维数组就行了。
4.最后一站:让我们来到经典背包问题
输入样例:
4 5
1 2
2 4
3 4
4 5
输出样例:
8
这个问题可能和前面的大盗阿福类似,还是在限制条件下求解最优解问题,我们老规矩,先来写经典的dfs版本:
#include
using namespace std;
const int maxn = 1005;
int N,V;
int w[maxn], v[maxn];
int dfs(int x, int surV)//surV表示当前背包的剩余体积,x表示当前正在考虑第x个物品
{
if (x > N)
return 0;
if (v[x] > surV)//该物品超出当前背包剩余体积,装不下,被迫继续寻找下一个物品
return dfs(x + 1, surV);
else if(surV>=v[x])
{
//能装下,但是我们可以自由选择装与不装
return max(dfs(x + 1, surV - v[x])+w[x], dfs(x + 1, surV));
}
}
int main()
{
cin >> N >> V;
for (int i = 1; i <= N; i++)
cin >> v[i] >> w[i];
cout << dfs(1, V) << endl;//从第一个物品开始考虑
return 0;
} 下面还是直接看动态规划版本:记忆化搜索就是个模板,不是太难理解,而且和dfs差距不大。
建议还是先理解前面正逆序方式的不同:
#include
using namespace std;
const int maxn = 105;
int N,V;
int dp[maxn][maxn];//第一个下标表示背包的当前选择的物品,第二个下标为当前背包剩余体积
int w[maxn], v[maxn];
int dfs(int x, int surV)
{
if (x > N)
return 0;
if (v[x] > surV)//该物品超出当前背包剩余体积,装不下,被迫继续寻找下一个物品
return dfs(x + 1, surV);
else if(surV>=v[x])
{
//能装下,但是我们可以自由选择装与不装
return max(dfs(x + 1, surV - v[x])+w[x], dfs(x + 1, surV));
}
}
int main()
{
cin >> N >> V;
for (int i = 1; i <= N; i++)
cin >> v[i] >> w[i];
倒推
//for (int i = N; i >= 1; i--)
//{
// for (int j = 0; j <= V; j++)
// {
// if (j < v[i])
// dp[i][j] = dp[i + 1][j];
// else if(j>=v[i])
// dp[i][j] = max(dp[i + 1][j], dp[i + 1][j - v[i]] + w[i]);//看到没,和我说的规律一样
// }
//}
// cout<= v[i])
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - v[i]] + w[i]);//看到没,和我说的规律一样
}
cout << dp[N][V] << endl;//终点在第N个物品
return 0;
} 5.总结
动态规划是一个上下限都极高的算法,想要学会并不容易,不知我这七千五百字能够让你们学到多少,动态规划算法的关键在于解决冗余,这是动态规划算法的根本目的。动态规划实质上是一种以空间换时间的技术,它在实现的过程中,不得不存储产生过程中的各种状态,所以它的空间复杂度要大于其他的算法。选择动态规划算法是因为动态规划算法在空间上可以承受,而搜索算法在时间上却无法承受,所以我们舍空间而取时间。
6.金句省身
不要期待突如其来的惊喜,更不要期待命运会突然得到改变。没有一蹴而就的成功,好运不过是努力的伏笔而已。真正让我们成长的力量,就藏在那些日复一日看似平常的坚持里。所以,不要抱怨,你只管努力,该来的成功不会远。
---------- 摘自《人民日报》