项目实训（七）——车辆寻路算法的实现

一、前言

在我们小组的项目的城市游戏场景中，我进行了车辆寻路的代码实现，该博客将简单记录一下工作内容。

二、代码实现

PathFinding:

using System.Collections;
using System.Collections.Generic;
using System;
using UnityEngine;
#if UNITY_EDITOR
using UnityEditor;
using UnityEditorInternal;
#endif

namespace PolyPerfect.City
{

    public class PathFinding : MonoBehaviour
    {
        private BinaryHeap Open =new BinaryHeap(2048);
        private Dictionary<Guid, int> OpenIDs = new Dictionary<Guid, int>();
        private Dictionary<Guid, PathNode> Closed = new Dictionary<Guid, PathNode>();
        [HideInInspector]
        public List<Path> PathList = new List<Path>();
        [HideInInspector]
        public List<Path> wholePath;

        private Vector3 startPoint;
        private Vector3 endPoint;

        private Tile endTile;
        private Tile startTile;
        private Guid endId;

         public List<Path> GetPath(Vector3 start, Vector3 end, PathType pathType)
         {
            Open.Clear();
            PathList = new List<Path>();
            Closed.Clear();
            OpenIDs.Clear();

            startPoint = start;
            endPoint = end;

            startTile = FindClosestTile(startPoint, pathType);
            endTile = FindClosestTile(endPoint, pathType);
            List<Path> startPaths;
            if(pathType == PathType.Sidewalk)
            {
                startPaths = startTile.sidewalkPaths;
            }
            else
                startPaths = startTile.paths;
            foreach (Path path in startPaths)
            {
                float h = CalculateHeuristic(path.pathPositions[path.pathPositions.Count - 1].position);
                float g = Vector3.Distance(transform.position, path.pathPositions[0].position) + Vector3.Distance(transform.position, path.pathPositions[path.pathPositions.Count-1].position);
                PathNode node = new PathNode() {path = path, lastNode = null, currentScore = g, score = h +g};
                Open.Insert(node);
                OpenIDs.Add(node.path.Id, 0);
            }
            if(DoBfsSteps())
            {
                Closed[endId].path = FindClosestPath(endPoint, Closed[endId].lastNode.path.nextPaths);
                GetPathList(Closed[endId]);
                PathList.Reverse();
                //PathList[0] = FindClosestPath(startPoint, startPaths);
                return PathList;
            }
            else
            {
                return null;
            }
         }
        public List<Path> GetPathWithCheckpoints(List<Vector3> checkpoints, PathType pathType)
        {
            wholePath = new List<Path>();
            
            for (int i = 1; i < checkpoints.Count ;i++)
            {
                startPoint = checkpoints[i-1];
                endPoint = checkpoints[i];
                Open.Clear();
                PathList = new List<Path>();
                OpenIDs.Clear();

                startTile = FindClosestTile(checkpoints[i-1], pathType);
                endTile = FindClosestTile(checkpoints[i], pathType);
                Closed.Clear();
                List<Path> startPaths;
                if (i == 1)
                {
                    if (pathType == PathType.Sidewalk)
                        startPaths = startTile.sidewalkPaths;
                    else
                        startPaths = startTile.paths;
                }
                else
                    startPaths = wholePath[wholePath.Count - 2].nextPaths;
                foreach (Path path in startPaths)
                {
                    float h = CalculateHeuristic(path.pathPositions[path.pathPositions.Count - 1].position);
                    float g = Vector3.Distance(transform.position, path.pathPositions[0].position) + Vector3.Distance(transform.position, path.pathPositions[path.pathPositions.Count - 1].position);
                    PathNode node = new PathNode() {path = path, lastNode = null, currentScore = g, score = h + g};
                    Open.Insert(node);
                    OpenIDs.Add(node.path.Id, 0);
                }
                if (DoBfsSteps())
                {
                    if(i == checkpoints.Count-1)
                        Closed[endId].path = FindClosestPath(checkpoints[i], Closed[endId].lastNode.path.nextPaths);
                    GetPathList(Closed[endId]);
                    PathList.Reverse();
                    //PathList[0] = FindClosestPath(startPoint, startPaths);
                    if(i>1)
                    {
                        wholePath.RemoveAt(wholePath.Count - 1);
                    }
                    wholePath.AddRange(PathList);
                }
                else
                {
                    return null;
                }
            }
            return wholePath;
        }
        private bool DoBfsSteps()
         {
                //int i = 0;
             while (Open.Count > 0)
             {

                PathNode node = GetBestNode();
               //Debug.Log(i++ + " " + (node.score) + " "+ node.path.transform.parent.parent.name);
                if (node.path.TileId == endTile.Id)
                {
                    Closed.Add(node.path.Id, node);
                    endId = node.path.Id;
                    return true;
                }
                foreach (Path item in node.path.nextPaths)
                {
                    if (item != null)
                    {
                        if(!Closed.ContainsKey(item.Id) && !OpenIDs.ContainsKey(item.Id))
                        {
                            Vector3 distance = item.pathPositions[0].position - item.pathPositions[item.pathPositions.Count-1].position;
                            float currentScore = node.currentScore + Math.Abs(distance.x) + Math.Abs(distance.y) + Math.Abs(distance.z) - ((item.speed /10) * item.transform.lossyScale.x);

                            Open.Insert(new PathNode() { path = item, lastNode = node, currentScore = currentScore, score = CalculateHeuristic(item.pathPositions[item.pathPositions.Count - 1].position) + currentScore });
                            OpenIDs.Add(item.Id, 0);
                        }
                    }
                }
                    Closed.Add(node.path.Id, node);

             }
            return false;
         }

        private PathNode GetBestNode()
        {
            
            PathNode pathNode = Open.PopTop();
            OpenIDs.Remove(pathNode.path.Id);
            return pathNode;
        }

        private float CalculateHeuristic(Vector3 currentTile)
        {
            Vector3 distance = endPoint - currentTile;
            return Math.Abs(distance.x) + Math.Abs(distance.y) + Math.Abs(distance.z);
        }
        private void GetPathList(PathNode thisNode)
        {
            if (thisNode != null)
            {
                PathList.Add(thisNode.path);
                GetPathList(thisNode.lastNode);
            }
        }

        private Tile FindClosestTile(Vector3 point, PathType pathType)
        {
            Tile closestTile = null;
            Collider[] coliders = Physics.OverlapBox(point, new Vector3(Mathf.Abs(2 * transform.lossyScale.x), Mathf.Abs(2 * transform.lossyScale.y), Mathf.Abs(2 * transform.lossyScale.z)));
            foreach (Collider collider in coliders)
            {
                closestTile = collider.transform.GetComponent<Tile>();
                if (closestTile != null)
                {
                    if (pathType == PathType.Road)
                    {
                        if(closestTile.tileType == Tile.TileType.Road || closestTile.tileType == Tile.TileType.RoadAndRail)
                        {
                            return closestTile;
                        }
                    }
                    else if(pathType == PathType.Rail)
                    {
                        if (closestTile.tileType == Tile.TileType.Rail || closestTile.tileType == Tile.TileType.RoadAndRail)
                        {
                            return closestTile;
                        }
                    }
                    else if (pathType == PathType.Sidewalk)
                    {
                        if (closestTile.tileType == Tile.TileType.Road || closestTile.tileType == Tile.TileType.OnlyPathwalk)
                        {
                            return closestTile;
                        }
                    }
                    
                }
            }
            float minDistance = Mathf.Infinity;
            
            foreach (Tile tile in Tile.tiles)
            {
                float distance = Vector3.Distance(tile.transform.position, point);
                if (distance < minDistance)
                {
                    if (pathType == PathType.Road)
                    {
                        if (tile.tileType == Tile.TileType.Road || tile.tileType == Tile.TileType.RoadAndRail)
                        {
                            minDistance = distance;
                            closestTile = tile;
                        }
                    }
                    else if (pathType == PathType.Rail)
                    {
                        if (tile.tileType == Tile.TileType.Rail || tile.tileType == Tile.TileType.RoadAndRail)
                        {
                            minDistance = distance;
                            closestTile = tile;
                        }
                    }
                    else if (pathType == PathType.Sidewalk)
                    {
                        if (tile.tileType == Tile.TileType.Road || tile.tileType == Tile.TileType.OnlyPathwalk)
                        {
                            minDistance = distance;
                            closestTile = tile;
                            
                        }
                    }
                   
                }
            }

            return closestTile;
        }
        private Path FindClosestPath(Vector3 point, List<Path> paths)
        {
            Path closestPath = null;
            float minDistance = Mathf.Infinity;
            foreach (Path path in paths)
            {
                for (int i = 0; i < path.pathPositions.Count; i++)
                {
                    float distance = Vector3.Distance(path.pathPositions[i].position, point);
                    if (distance < minDistance)
                    {
                        minDistance = distance;
                        closestPath = path;
                    }
                }
            }
            return closestPath;
        }
    }
    #region Editor
#if UNITY_EDITOR
    [CustomEditor(typeof(PathFinding)), CanEditMultipleObjects]
    public class CustomPathEditor : Editor
    {
        PathFinding navPath;
        private void OnEnable()
        {
            navPath = target as PathFinding;
        }
        void OnSceneGUI()
        {
            if (navPath.wholePath.Count == 0)
            {
                if (navPath.PathList.Count != 0)
                {
                    for (int i = 0; i < navPath.PathList.Count; i++)
                    {
                        if (navPath.PathList[i] != null)
                        {
                            if (i < navPath.PathList.Count - 1)
                            {
                                for (int j = 1; j < navPath.PathList[i].pathPositions.Count; j++)
                                {
                                    Handles.color = Color.white;
                                    Handles.DrawLine(navPath.PathList[i].pathPositions[j - 1].position, navPath.PathList[i].pathPositions[j].position);
                                    Handles.color = Color.blue;
                                    Handles.ArrowHandleCap(0, navPath.PathList[i].pathPositions[j - 1].position, Quaternion.LookRotation(navPath.PathList[i].pathPositions[j].position - navPath.PathList[i].pathPositions[j - 1].position), 3f, EventType.Repaint);
                                    if (i == 0)
                                        Handles.color = Color.blue;
                                    else if (i == navPath.PathList.Count - 1)
                                        Handles.color = Color.red;
                                    else
                                        Handles.color = Color.white;
                                    Handles.SphereHandleCap(0, navPath.PathList[i].pathPositions[j].position, Quaternion.LookRotation(navPath.PathList[i].pathPositions[j].position), 0.2f, EventType.Repaint);
                                }

                            }
                        }

                    }
                }
            }
            else 
            {
                for (int i = 0; i < navPath.wholePath.Count; i++)
                {
                    if (navPath.wholePath[i] != null)
                    {
                        if (i < navPath.wholePath.Count - 1)
                        {
                            for (int j = 1; j < navPath.wholePath[i].pathPositions.Count; j++)
                            {
                                Handles.color = Color.white;
                                Handles.DrawLine(navPath.wholePath[i].pathPositions[j - 1].position, navPath.wholePath[i].pathPositions[j].position);
                                Handles.color = Color.blue;
                                Handles.ArrowHandleCap(0, navPath.wholePath[i].pathPositions[j - 1].position, Quaternion.LookRotation(navPath.wholePath[i].pathPositions[j].position - navPath.wholePath[i].pathPositions[j - 1].position), 3f, EventType.Repaint);
                                if (i == 0)
                                    Handles.color = Color.blue;
                                else if (i == navPath.wholePath.Count - 1)
                                    Handles.color = Color.red;
                                else
                                    Handles.color = Color.white;
                                Handles.SphereHandleCap(0, navPath.wholePath[i].pathPositions[j].position, Quaternion.LookRotation(navPath.wholePath[i].pathPositions[j].position), 0.2f, EventType.Repaint);
                            }

                        }
                    }

                }
            }
            
        }
    }
#endif
    #endregion
}

三、算法学习

A*算法

虽然在unity给我们的提供了Navigation作为我们寻路的解决方案，但是在实际中我们同样也不得不使用到一套自己的方案来实现，这时A就是我们最常用的一种方式。
A 搜索算法是一种解决图遍历问题的计算机算法，这是一种在图形平面上，有多个节点的路径，求出最低通过成本的算法。最主要的应用是寻找地图中两点间的最佳路线。
A改变它自己行为的能力是基于启发式代价函数*，启发式代价函数在速度和精确度之间取得折中会让游戏运行得更快。
在介绍启发式搜索算法之前，先介绍状态空间搜索。状态空间搜索就是将一个问题的求解表现为从初始状态到目标状态的过程。 在这个过程中，我们可以使用树这种数据结构去表达，由于求解方式有很多（树的分支）我们到达目标状态的方式也就有很多，这个过程就叫做状态空间搜索。
状态空间搜索也分为：深度优先和广度优先。
广度优先是从初始状态一层一层向下找直到找到为止。
深度优先是按照一定的顺序查找完一个分支再去查询另一个分支，直到找到为止。
深度优先和广度优先算法在状态空间不大的时候会很合适的，但是如果状态空间非常大并且不可预测的情况下就不可取了。它的效率会十分的低，甚至无法完成。 这时就需要用到启发式搜索。
启发式搜索算法：
启发式搜索算法就是在状态空间中对每一条搜索分支进行评估，得到最好的分支，再从这个分支进行搜索从而到达目标。这样可以省略大量无畏的搜索路径，提高效率。
在这其中，对分支的评估是非常重要的，不同的评估就会有不同的效果。以下为部分评估算法：
局部择优搜索： 在搜索过程中，选取在该层分支中的“最佳节点”后舍弃其他兄弟节点，父节点，而一直进行搜索下去。由于舍弃了其他节点，也很可能也把全局的最佳节点也舍去。
最好优先搜索：为局部择优的优化版，在搜索时，找到最佳节点后并不是舍弃其他节点，在每一次评估中都把当前的节点和以前的节点的估价值进行比较得到一个最佳节点。
A算法： A ** 算法也属于一种最好优先算法，但是为进行一些条件约束。因为在某些问题的求解时，我们希望求解出状态空间搜索的最短路径，也就是用最快的方案求解问题。 我们先对问题做一个定义，如果一个评估方法可以找出最短路径，我们称之为可采纳性。A 算法是一个可采纳的最好优先算法。
估价函数
启发中的估价是用估价函数表示的：
             f（n）=g（n）+h（n）

其中f（n）是节点n的估价函数，g（n）是在状态空间中从初始节点到n节点的实际代价，h（n）是从n到目标节点最佳路径的估价代价。在这里主要是h（n）体现了搜索的启发信息，因为g（n）是已知的。g（n）就代表了搜索的广度优先趋势。但是当h（n）>g（n）时，可以省略g（n），而提高效率。
像素化地图。
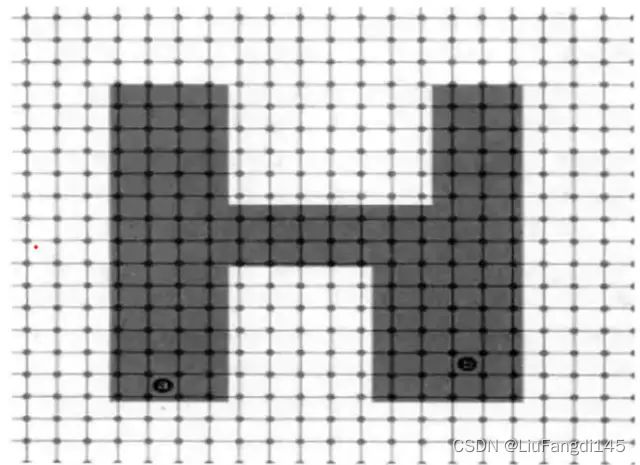
我们想要进行对AI路径的控制首先我们就需要对地图进行像素化。 何为像素化地图呢？ 就如unity的网格一样。将一张地图按照一定的比例尺进行网格化划分就是像素化。其中的每一个网格单元我们称之为节点（不以方格来表示示因为这些网格单元不一样是矩形的也可以是六边形，圆形等等。）。节点就称为是寻路算法的单元。
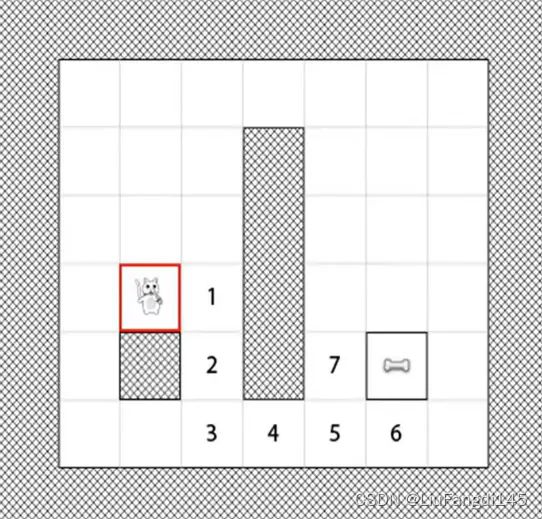
示例图片：

使用了正方形作为了寻路算法单元

可视化导航点

导航网格，可行走区域划分为凸多边形。

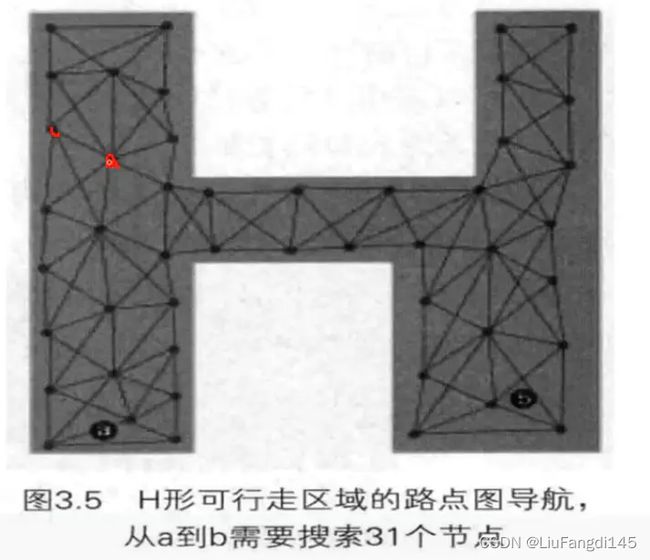
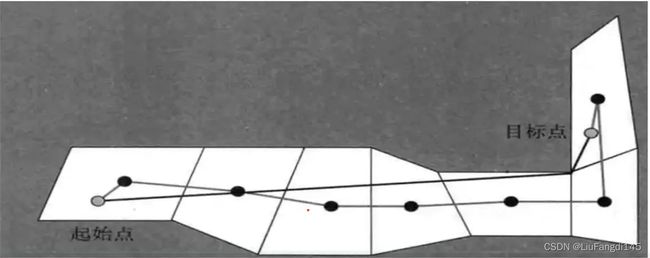
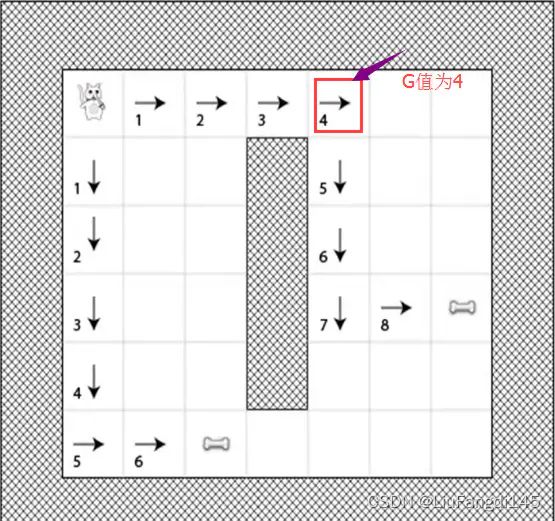
寻路的第一步是简化成易控制的搜索区域。
接着我们就需要模拟计算出寻路的最短路径。

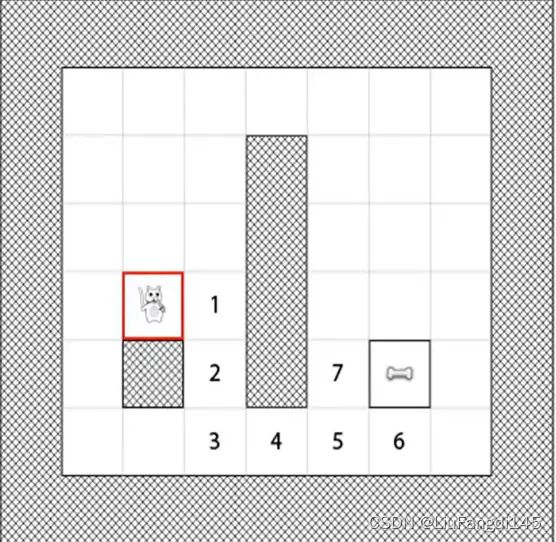
从我们的角度去思考，猫到食物的最短路径有两条。

1-2-3-4-5-6-食物
1-2-3-4-5-7-食物
那计算机是如何处理的呢？

我们在计算最短路径的时候最关键的部分也就是计算出距离！。
而这个距离并不是直线距离，是曼哈顿距离。

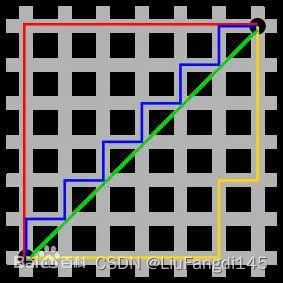
曼哈顿距离

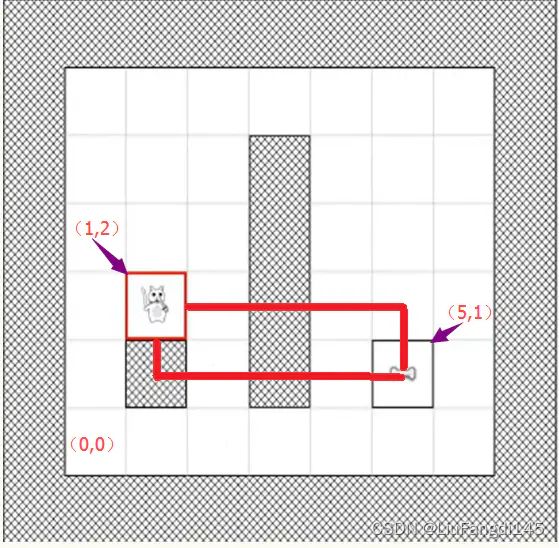
曼哈顿距离是一种使用在几何度量空间的几何学用语，用以标明两个点在标准坐标系上的绝对轴距总和。图中红线代表曼哈顿距离，绿色代表欧氏距离，也就是直线距离，而蓝色和黄色代表等价的曼哈顿距离。

曼哈顿距离：两点在X轴方向上的距离加上两点在Y轴方向上的距离。
例如在平面上，坐标（x1, y1）的i点与坐标（x2, y2）的j点的曼哈顿距离为：

d(i,j)=|X1-X2|+|Y1-Y2|

以上图猫的地图来说：

以左下角的方格为（0,0）点，那猫的坐标就为（1,2），食物的坐标为（5,1），那它们的曼哈顿距离就为d（i，j）=|1-5|+|2-1|=5. 图中两条红线就是曼哈顿距离。（没有考虑障碍物的情况）

f值， f（n），估价值函数。要想从起点A到B，中间可能经过n个点，假如其中经过点x，则对点x的计算所得的估价值就是f（x），估价值越小越好。

g值： 从起点A到达x点实际所花费的价值。以方格为例，g值就表示，从A到x点的格子数。

h值，从点X到终点B可能需要花费的值，所谓的估计值。f（x）=g（x）+h（x），g（x）是固定的，要想f（x）越小那h（x）就得越小。
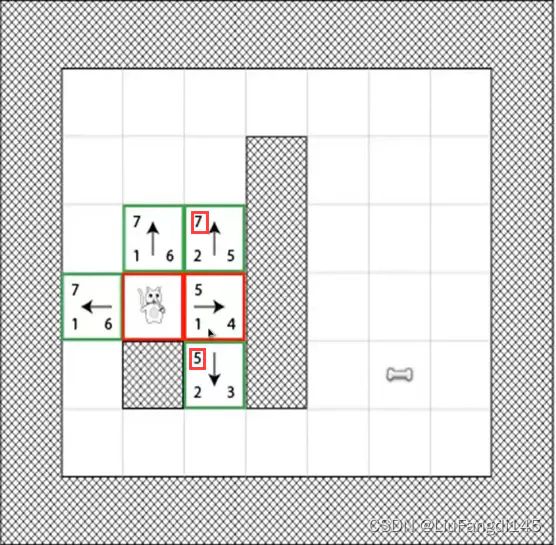
寻路算法。

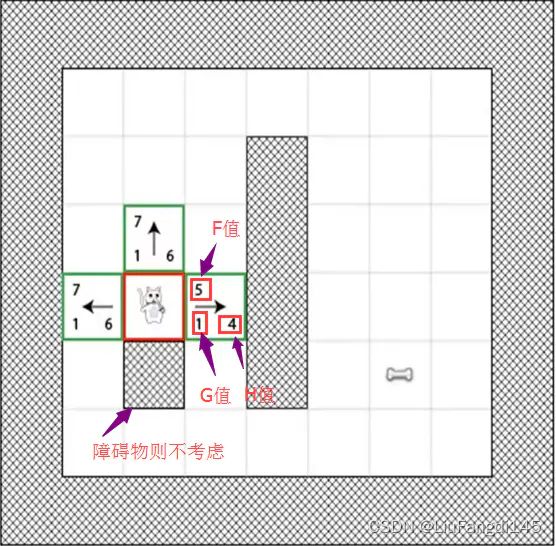
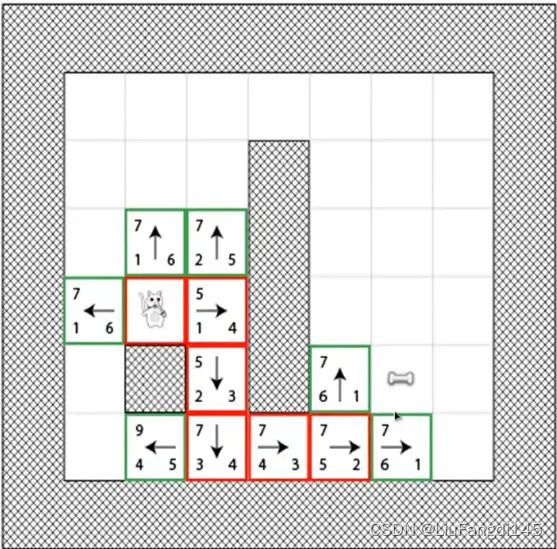
如图所示，由于猫的下方有障碍物，则猫的移动方向有三个方向。F值分别为5,7,7，那就会选择F值较小也就是5的这条路径进行移动。

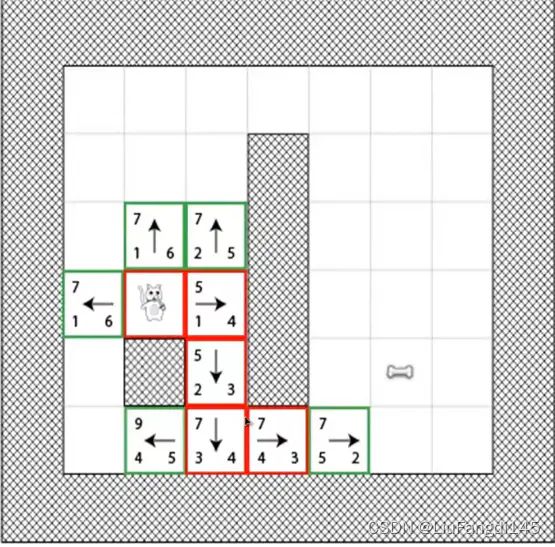
移动以后。则有出现了5,7两条路线，继续选择5的路径进行移动

但当我们发现在继续移动时，就会出现以下问题，我们开始选择的最佳路径，到了此时却出现了四条估值都为7的路径。

我们先继续沿着路径行走。

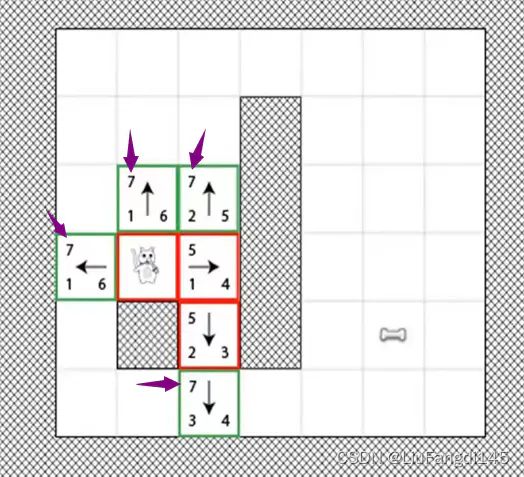
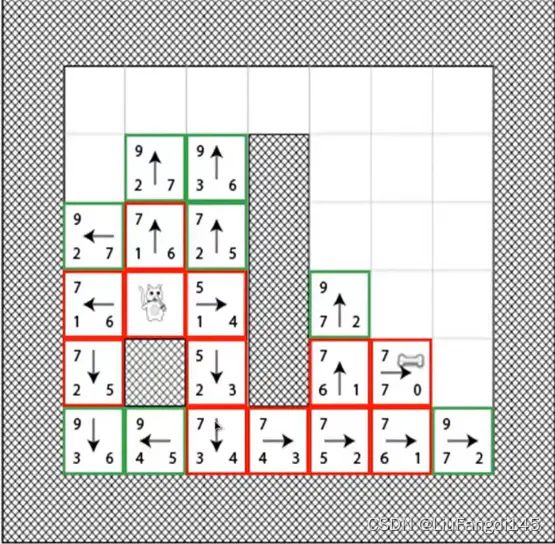
最终我们得到了两条最短路径。（之前我们没有用计算机考虑的路径）

如果没有沿着之前最近的点进行移动。（通过模拟测试其他路线的估值将会更大）

使用算法进行实现。（Open列表和Close列表）
首先我们需要一个列表用于保存检索出所有可行走的路线（Open列表）。当我们通过一个路径时需要知道这条路径是否被检索过。（Close列表）

Open列表：记录所有被考虑来寻找最短路径的方块。
Close列表：记录下不会再被考虑的方块。
猫寻路的步骤：

将方块添加到open列表，该列表中有最小的F值，将这个方块进行标记为S。
将S从open列表移除，然后添加到closed列表中。
对与S相邻的每一块可通行的方块标记为T。
如果T在closed列表中，则不进行考虑。
如果T不在open列表里，添加它然后计算出F值。
如果T已经在open中，使用当前生成的路径到达那里时，检查F值是否更小。如果是，更新它的F值并前进。

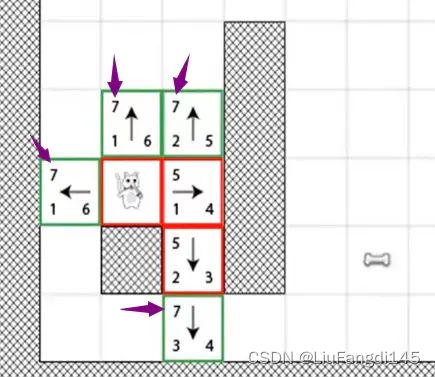
当遇见这种有多个相同F值的分叉路径时，我们需要一个父节点来记录行走过的路，进行路径的回溯。

伪代码：