R语言dlnm包在时间序列数据的分布滞后线性和非线性模型的应用(1)
气温对健康影响的滞后性已得到公认。本期通过dlnm包来介绍一下dlnm包在时间序列数据的分布滞后线性和非线性模型的应用。Dlnm包通过构建构建交叉基矩阵来进行分析。
我们继续使用美国芝加哥1987年至 2000年大气污染与死亡数据(公众号回复:芝加哥3,可以获得数据)做实例分析,我们先导入需要的R包和数据看看
library(dlnm)
library(splines)
library(tsModel)
bc<-read.csv("E:/r/test/chicago3.csv",sep=',',header=TRUE)
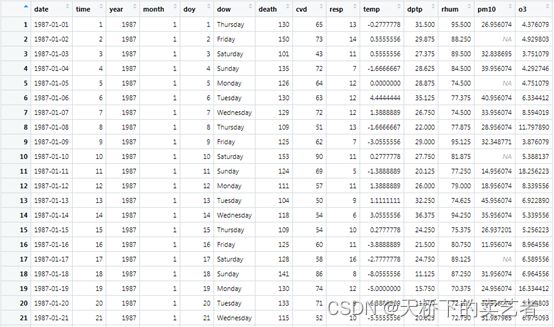
我们先来看看数据的构成,death:死亡人数 (per day),pm10:大气污染物pm10的中位数值,o3median:臭氧的中位数值,time:天数,这里就是我们的时间,tmpd:华氏温度,date:日期
假设我们需要研究pm10浓度变化对死亡的影响,并且要把温度作为调整因素,这样我们要设计两个交叉基的矩阵。Crossbasis函数我来解释一下,第一个参数x是用来指定矢量序列的,这里填入bc$pm10,lag这里表示的是滞后天数,填入15天,argvar and arglag这两个函数会把数据传递给一个onebasis的函数,生成预测的矩阵,这里假设pm10对结局的影响是线性的,使用fun=“lin”,后面采用多项式函数fun=“poly”,自由度设置为4。如果我们不对fun进行选择,函数默认fun=“ns”,下面温度就是这样,我们还可以选择一个温度参考值,如我们选择21度,argvar = list(fun = “ns”,df =3,cen =21)。"strata"是分层的意思,因为我们设置的是滞后3天,因此breaks=1,就是把温度分为两个滞后层(0-1和1-3)两个滞后层。
cb1.pm <- crossbasis(bc$pm10, lag=15, argvar=list(fun="lin"),
arglag=list(fun="poly",degree=4))
cb1.temp <- crossbasis(bc$temp, lag=3, argvar=list(df=5),
arglag=list(fun="strata",breaks=1))
我们summmary cb1.pm一下看看
model1 <- glm(death ~ cb1.pm + cb1.temp + ns(time, 7*14) + dow,
family=quasipoisson(), chicagoNMMAPS)
生成cb1.pm的预测数据
pred1.pm <- crosspred(cb1.pm, model1, at=0:20, bylag=0.2, cumul=TRUE)
at=0:20表示必须对0到20µgr/m 3的每个整数值进行预测计算,通过设置bylag=0.2,预测是沿着滞后空间计算的,增量为0.2。增量为0.2。这种更细的网格是为了在绘制结果时产生一个更平滑的滞后曲线。如果没有进行参数cen设置,默认的参考值是0.
生成了预测数据以后就可以绘图了,先绘制一个pm10滞后与死亡关系图,"slices"表示绘图类型,var=10表示关系,没设定参考值的话是以0为参考。Var设定必须在"slices"这种类型才可以。ci.arg用于绘制置信区间。
plot(pred1.pm, "slices", var=10, col=3, ylab="RR", ci.arg=list(density=15,lwd=2),
main="Association with a 10-unit increase in PM10")
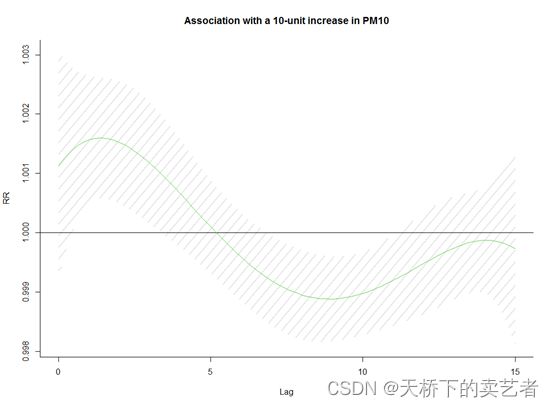
本图表示pm10增加10 µgr/m与死亡率的滞后关联。滞后曲线代表了在增加10微克后未来每一天的风险增加。滞后曲线表示在某一天PM10增加10 µgr/m 3后,未来每一天的风险增加,或者说是过去每一天的PM10增加对某一天的风险的贡献。
接下来绘制一个pm10累积增加的风险图,
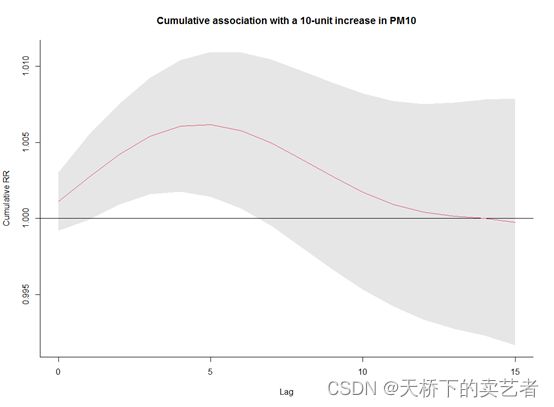
plot(pred1.pm, "slices", var=10, col=2, cumul=TRUE, ylab="Cumulative RR",
main="Cumulative association with a 10-unit increase in PM10")
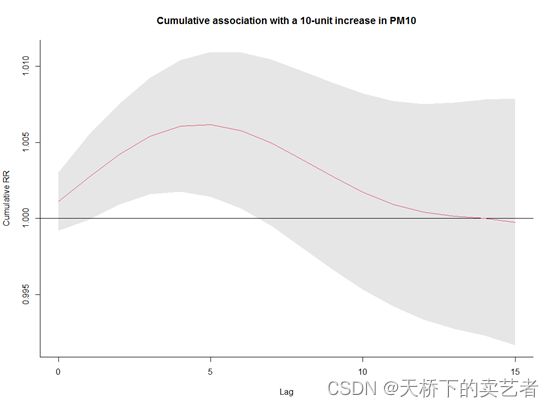
图表明,PM10最初的风险增加在较长的滞后期会被逆转。相关数据可以使用allRRfit, allRRhigh and allRRlow提取。
