双因素方差分析_R语言统计篇:双因素方差分析
点击蓝字就可以关 注" R语言与统计 "哦~~ 今天的内容小编只想说:加油! 
在往期的文章里,介绍过单因素方差分析[R语言统计篇:单因素方差分析],今天介绍 双因素方差分析(Two-way ANOVA) 。 此方法用于检验两个分类变量(自变量)与一个连续变量(因变量)之间的关系。 比方说,如果一个分类变量有两个组别,另外一个分类变量有三个组别,那么一共就有2×3( = 6)个组别。根据各组之间的样本量是否相等,双因素方差分析又可分为 均衡设计(Balanced design)与非均衡设计(Unbalanced design) 。 此篇文章会先介绍均衡设计,末尾再补上非均衡设计 。 与所有的方差分析一样,双因素方差分析的使用也需要满足 几个前提 :
此研究一共包含60只豚鼠,每只豚鼠通过两种给药方式( supp : OJ与VC)给予三种不同剂量的维生素C( dose : 0.5, 1, 2 mg/day)。 首先查看基本内容: 从上述可知,此数据集包含60行*3列的数据。
从上述可知,此数据集包含60行*3列的数据。
其中, supp 是一个两水平(2 levels)的分类变量(factor);变量 dose 在R中是以数值型(num)变量的形式保存。
而双因素方差分析要求 两个自变量均为分类变量 (categorical variable或factor),所以应将 dose 转换为factor的形式,以备后续分析使用。 下一步,查看一下6组间的样本量各是多少:
下一步,查看一下6组间的样本量各是多少:

 从上图中基本可以了解到,不同的剂量(dose)与不同的给药方式(supp)可能都会对牙齿的生长(len)有影响,并且可能存在交互作用。 下一步进行统计分析。
从上图中基本可以了解到,不同的剂量(dose)与不同的给药方式(supp)可能都会对牙齿的生长(len)有影响,并且可能存在交互作用。 下一步进行统计分析。 



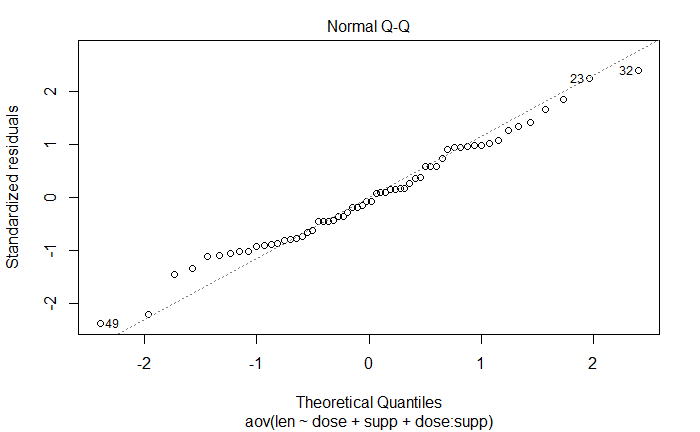 所有的点大体上分布在对角线上,提示:没有违反正态性的原则。
所有的点大体上分布在对角线上,提示:没有违反正态性的原则。


 让R语言与统计更简单
让R语言与统计更简单 对我们最好的鼓励就是点赞,关注与转发哦!
对我们最好的鼓励就是点赞,关注与转发哦!


在往期的文章里,介绍过单因素方差分析[R语言统计篇:单因素方差分析],今天介绍 双因素方差分析(Two-way ANOVA) 。 此方法用于检验两个分类变量(自变量)与一个连续变量(因变量)之间的关系。 比方说,如果一个分类变量有两个组别,另外一个分类变量有三个组别,那么一共就有2×3( = 6)个组别。根据各组之间的样本量是否相等,双因素方差分析又可分为 均衡设计(Balanced design)与非均衡设计(Unbalanced design) 。 此篇文章会先介绍均衡设计,末尾再补上非均衡设计 。 与所有的方差分析一样,双因素方差分析的使用也需要满足 几个前提 :
1. 残差需符合正态或接近正态分布。
2. 各组别的方差相同,即方差齐性。
1. 均衡设计的双因素方差分析(各组间样本量相等)
1.1 准备数据
今天使用到的数据是R自带的“ ToothGrowth” ,是研究维生素C对于豚鼠牙齿生长的影响。此研究一共包含60只豚鼠,每只豚鼠通过两种给药方式( supp : OJ与VC)给予三种不同剂量的维生素C( dose : 0.5, 1, 2 mg/day)。 首先查看基本内容:
summary(ToothGrowth)
## len supp dose
## Min. : 4.20 OJ:30 Min. :0.500
## 1st Qu.:13.07 VC:30 1st Qu.:0.500
## Median :19.25 Median :1.000
## Mean :18.81 Mean :1.167
## 3rd Qu.:25.27 3rd Qu.:2.000
## Max. :33.90 Max. :2.000str(ToothGrowth)
#'data.frame': 60 obs. of 3 variables:
# $ len : num 4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
# $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
# $ dose: num 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 0.5 ...
其中, supp 是一个两水平(2 levels)的分类变量(factor);变量 dose 在R中是以数值型(num)变量的形式保存。
而双因素方差分析要求 两个自变量均为分类变量 (categorical variable或factor),所以应将 dose 转换为factor的形式,以备后续分析使用。
mydata mydata$dose
# 查看dose是否已经转为为factor
str(mydata)
#'data.frame': 60 obs. of 3 variables:
# $ len : num 4.2 11.5 7.3 5.8 6.4 10 11.2 11.2 5.2 7 ...
# $ supp: Factor w/ 2 levels "OJ","VC": 2 2 2 2 2 2 2 2 2 2 ...
# $ dose: Factor w/ 3 levels "0.5","1","2": 1 1 1 1 1 1 1 1 1 1 ...
table(mydata$supp, mydata$dose)
# 0.5 1 2
# OJ 10 10 10
# VC 10 10 10
1.2 作图
双因素方差分析可以选择的作图方式有很多,这里介绍 箱形图 [R语言画展ggplot2篇-箱形图]。library(ggplot2)
ggplot(mydata, aes(dose, len, color = supp)) +
geom_boxplot()
 从上图中基本可以了解到,不同的剂量(dose)与不同的给药方式(supp)可能都会对牙齿的生长(len)有影响,并且可能存在交互作用。 下一步进行统计分析。
从上图中基本可以了解到,不同的剂量(dose)与不同的给药方式(supp)可能都会对牙齿的生长(len)有影响,并且可能存在交互作用。 下一步进行统计分析。 1.3 双因素方差分析的计算
首先,拟合只包含主效应的的方程,此类方程假定dose与supp之间是相互独立的。
# 未包含dose:supp的交互项
myaov_1 summary.aov(myaov_1)
# Df Sum Sq Mean Sq F value Pr(>F)
#dose 2 2426.4 1213.2 82.81 < 2e-16 ***
#supp 1 205.4 205.4 14.02 0.000429 ***
#Residuals 56 820.4 14.7
#---
#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## 添加dose:supp的交互项
myaov_2 summary.aov(myaov_2)
# Df Sum Sq Mean Sq F value Pr(>F)
#dose 2 2426.4 1213.2 92.000 < 2e-16 ***
#supp 1 205.4 205.4 15.572 0.000231 ***
#dose:supp 2 108.3 54.2 4.107 0.021860 *
#Residuals 54 712.1 13.2
#---
#Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
1.4 结果解释
如果将p值设定在0.05,我们可以得出以下结论: ① supp的p值为0.00049,提示不同的给药方式与不同的牙齿长度有关。 ② dose的p值为<2e-16,提示不同的药物剂量与不同的牙齿长度有关。 (注:上述变量的p值来自myaov_1,而不是myaov_2) ③ dose与supp交互项的p值为0.02, 提示给药剂量与牙齿长度之间的关系随着给药方式的不同而改变。1.5 多重比较
从上述ANOVA的结果可知某些组别之间存在统计学差异,但并不知具体哪对组别之间存在统计学差异。 因此,下一步进行多重比较,我们选择的是经典的 Tukey HSD :上述呈现了各个组别之间的两两比较结果。TukeyHSD(myaov_2, which = "dose:supp")#Tukey multiple comparisons of means
# 95% family-wise confidence level
#Fit: aov(formula = len ~ dose + supp + dose:supp, data = mydata)
#$`dose:supp`
diff lwr upr p adj
#1:OJ-0.5:OJ 9.47 4.671876 14.2681238 0.0000046
#2:OJ-0.5:OJ 12.83 8.031876 17.6281238 0.0000000
#0.5:VC-0.5:OJ -5.25 -10.048124 -0.4518762 0.0242521
#1:VC-0.5:OJ 3.54 -1.258124 8.3381238 0.2640208
#2:VC-0.5:OJ 12.91 8.111876 17.7081238 0.0000000
#2:OJ-1:OJ 3.36 -1.438124 8.1581238 0.3187361
#0.5:VC-1:OJ -14.72 -19.518124 -9.9218762 0.0000000
#1:VC-1:OJ -5.93 -10.728124 -1.1318762 0.0073930
#2:VC-1:OJ 3.44 -1.358124 8.2381238 0.2936430
#0.5:VC-2:OJ -18.08 -22.878124 -13.2818762 0.0000000
#1:VC-2:OJ -9.29 -14.088124 -4.4918762 0.0000069
#2:VC-2:OJ 0.08 -4.718124 4.8781238 1.0000000
#1:VC-0.5:VC 8.79 3.991876 13.5881238 0.0000210
#2:VC-0.5:VC 18.16 13.361876 22.9581238 0.0000000
#2:VC-1:VC 9.37 4.571876 14.1681238 0.0000058
1.6 查看是否符合检验的前提
ANOVA要求残差需符合正态分布以及各组间的方差相等。 如果违反了这些前提,那我们上述所得的结论都会显得不可靠。在写报告或者发表论文时,添加检验的内容会增加研究结果的可靠性。 第一步 :检验残差是否符合正态分布,将会使用到{car}包里面的leveneTest():library(car)
leveneTest(len ~ dose*supp, data = mydata)
##Levene's Test for Homogeneity of Variance (center = median)
## Df F value Pr(>F)
##group 5 1.7086 0.1484
## 54
plot(myaov_2, 2)
 所有的点大体上分布在对角线上,提示:没有违反正态性的原则。
所有的点大体上分布在对角线上,提示:没有违反正态性的原则。
2. 非均衡设计的双因素方差分析(各组间样本量不等)
如果各组间的样本量不等,操作方式有些许不同,将会使用到{car}包中的Anova()( 注:Anova中的A要大写 ),见下方代码:library(car)
my_model Anova(my_model, type = "III")##Anova Table (Type III tests)
##Response: len
Sum Sq Df F value Pr(>F)
##(Intercept) 1750.33 1 132.730 3.603e-16 ***
##dose 885.26 2 33.565 3.363e-10 ***
##supp 137.81 1 10.450 0.002092 **
##dose:supp 108.32 2 4.107 0.021860 *
##Residuals 712.11 54
##---
##Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

好啦,今天的内容就到这里~~
![]()

 让R语言与统计更简单
让R语言与统计更简单 对我们最好的鼓励就是点赞,关注与转发哦!
对我们最好的鼓励就是点赞,关注与转发哦!
❤好文,点个在看吧