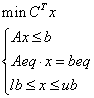数学建模学习笔记——线性规划

本文章为《数学建模算法与应用（司守奎）》书籍的学习笔记，文章内代码大部分为该书籍的搬运，主要目的为简化阅读的过程，以便直接实现代码的运用，我也会对书中的习题给出自己的解。

一、基础知识储备

1.线性规划

1.1标准形式

%标准型式直接使用matlab自带函数
%[x,favl] = linprog(C,A,b);
%[x,favl] = linprog(C,A,b,Aeq,beq);
%[x,favl] = linprog(C,A,b,Aeq,beq,lb,ub);注意可能有隐含自变量取值非负。
%x为目标函数取得最优时的变量取值，favl为目标函数的最优值，linprog只能求解形式如上的线性规划，如果是max，则对目标函数取负，最后的结果再取负。
%约束条件也必须取负变成小于等于的形式。

1.2非标准形式

非标准形式的线性规划有绝对值型和最大最小型/最小最大型两种情况。

• 绝对值型
  
  对于绝对值型，经过转化后可以直接应用matlab自带的函数进行求解。
• 最大最小型/最小最大型
  
  对于最值-最值型，一般的解题思路都是二分法求解，先给定一个t，看t是否满足约束条件（可行性检验），即取t时，线性规划是否有解，根据是否有解的情况，对搜索的区间进行二分，最终t会收敛到一个给定的值，该值即是满足条件的最优解。

%我写这部分时，不知道用二分法求解线性规划模型时的可行性检验怎么写，不过很幸运，matlab是真的6，我找到了求最大值最小化的函数fminimax()
%该程序以书本上的模型二为例
waw = @(x)[-0.025*x(2),-0.015*x(3),-0.055*x(4),-0.026*x(5)];	%目标函数，因为fminimax默认求最小值最大化，所以对每一个函数取负，x(1)表示对银行的投资额，风险为0,所以一定不会参与到最小值最大化，所以这里不写出。

x0 = [0.2 0.2 0.2 0.2 0.2]';
A = [-0.05 -0.27 -0.19 -0.185 -0.185];
Aeq = [1 1.01 1.02 1.045 1.065];

for i = 0.01:0.01:0.2	%对收益从0.01~0.2以步长0.01取值，对多约束的线性规划求解，favl求得的值为风险度的相反数，取负则得到每一种投资的风险度。
[x favl] = fminimax(waw,x0,A,-i,Aeq,1,zeros(5,1))
end

%给定初始值x0，函数搜索到一个最近的最优值（可能为局部最优值），求解无约束最优值的函数有fminunc(),fminsearch(),具体用法请自行查看官方文档。

1.3多目标规划

多目标规划有传统解法和遗传算法，传统解法包括线性加权法、优先级法、理想点法。
多目标规划标准型：

• 线性加权法
  
• 优先级法
  
• 理想点法（非线性规划，当解空间非凸时，常常得到局部最优解）
  

代码实现
问题：

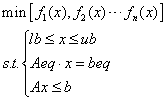
%线性加权法
X = [];
F = [];
for alpha = 0:0.01:1%alpha表示Z1的权重
    c = [4*(1-alpha)-9*alpha,5*(1-alpha)-10*alpha,8*(1-alpha)-14*alpha];
    A = [2 8 6;4 4 6;7 6 8];
    b = [40;50;80];
    [x,favl] = linprog(c,A,b,[],[],zeros(3,1));
    X = [X x];
    F = [F favl];
end
table = [[0:0.01:1]' X' F'];
fprintf('alpha\t')
for i = 1:size(x,1)
    fprintf('X(%d)\t',i);
end
fprintf('F\t\n');
for i = 0:100
    fprintf('%.2f\t',table(i+1,:));
    fprintf('\n');
end

%优先级法，理想点法略

%遗传算法,matalb有自带的遗传算法，可以实现多目标优化，具体自己如何实现遗传算法等到时间充裕了再好好研究吧
%新建.m文件
function y = fittness(x)

y = zeros(2,1);
y(1) = -9*x(1)-10*x(2)-14*x(3);
y(2) = 4*x(1)+5*x(2)+8*x(3);

end
%具体gamultiobj函数的用法请自己查询官方文档
[x,fval] = gamultiobj(@fittness,3,[2 8 6;4 4 6;7 6 8],[40;50;80],[],[],zeros(3,1),[])

2.运输问题

某商品有m 个产地、n 个销地，各产地的产量分别为a1,…,am ，各销地的需求量分别为b1,…,bn 。若该商品由i 产地运到 j 销地的单位运价为cij ，问应该如何调运才能使总运费最省？

对该问题的目标函数和约束条件进行变形，可得标准线性规划形式。

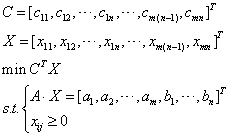
生成系数矩阵A的代码如下：

%新建一个.m文件生成系数矩阵
function A = portA( m,n )
%portA 生成运输类问题的系数矩阵，原问题C矩阵为m行，n列
A = zeros(m+n,m*n);
for i = 1:m
    A(i,n*i-n+1:n*i)=ones(1,n);
end
for i = m+1:n+m
    A(i,i-m:n:n*m) = 1;
end
end

生成系数矩阵之后，原问题就可以转化为一般的线性规划问题直接求解。

3.指派问题

指派问题可以看做是特殊的运输问题，此时xij取0或1，m=n,ai=bj=1。

4.对偶理论与灵敏度分析

说实话，运筹学我没学过啊啊，这里也不懂诶，贴上一个B站up的链接。
这部分的内容主要包括以下几个方面：

• 线性规划与对偶线性规划相互转化
• 对偶问题的性质：对称性、弱对偶性、无界性、最优性、对偶理论、互补松弛性
• 灵敏度分析（某一个量改变最优解的变化情况）：价值系数cj的灵敏度分析、资源限量bi的灵敏度分析、技术系数aij的灵敏度分析

主要用到的是单纯形法和对偶单纯形法。

二、章节习题解答

Q3

Q4

%新建.m文件求系数矩阵
function A = portA2( Ain)
%portA 生成运输类问题的系数矩阵，原问题C矩阵为m行，n列
[m,n] = size(Ain);
A = zeros(m,m*n);
for i = 1:m
    for j = i:m:n*m
        A(i,j) = Ain(i,(j-i+m)/m);
    end
end
end

A = [5 10 0;7 9 12;6 8 0;4 0 11;7 0 0];
A = portA2(A);
C = [1 1 1 0 0 0 0 1.65 0 0 0 2.3 0 0 0].*(-1);
b = [6000;10000;4000;7000;4000];
Aeq = [1 1 -1 -1 -1 0 0 0 0 0 0 0 0 0 0;0 0 0 0 0 1 1 -1 0 0 0 0 0 0 0;0 0 0 0 0 0 0 0 0 0 0 1 0 -1 0];
beq = [0;0;0];
lb = zeros(15,1);
ub = [inf inf inf inf inf inf inf inf 0 0 0 inf 0 inf 0]';
[x y] = intlinprog(C,1:15,A,b,Aeq,beq,lb,ub)%该问题是一个整数规划问题
%最终所得的y值的相反数即为目标函数不包括常数项的最大值
%题外话，这个解出来的最优解有点小感觉，好像开工厂加工并不怎么赚钱，dog

Q5

%portA函数请看运输问题部分代码

Aeq = portA(4,4);
C = [15 18 21 24 19 23 22 18 26 17 16 19 19 21 23 17];
beq = ones(8,1);
[x favl] = intlinprog(C,1:16,[],[],Aeq,beq,zeros(16,1),ones(16,1)); %还是一个整数规划
X = reshape(x,[4,4])' %最终的X即为指派矩阵

Q6

C = [0.1 0.20 0.15 0.25 0.08 0.16 0.12 0.20];
A = [1 1 1 1 0 0 0 0;0 0 0 0 1 1 1 1;450/2+450/4+200 480/2+480/4+200 540/2+540/4+200 600/2+600/4+200 450/3+450/4+200 480/3+480/4+200 540/3+540/4+200 600/3+600/4+200];
b = [48 32 48000]';
C = C.*-1;
[x favl] = intlinprog(C,1:8,A,b,[],[],zeros(8,1));
X = reshape(x,[4,2])
favl = -favl
%favl为可以摧毁敌方军事基地的导弹的最大期望值

Q8

C = [1 1 2 2 3 3 4 4];
Aeq = [1 -1 -1 1 -1 1 1 -1;1 -1 -1 1 1 -1 -3 3;1 -1 -1 1 -2 2 3 -3];
beq = [0 1 -0.5];
lb = zeros(8,1);
[uv favl] = linprog(C,[],[],Aeq,beq,lb);
X = [uv(1:2:8)-uv(2:2:8)] %X为自变量的取值

Q9

%说实话不想敲了，和前面的题都差不多