【C++】AVL树,红黑树
上一篇博客,我们深入讨论了map/multimap,set/multiset的使用和注意事项,让我们提到关联式容器,还有他们的底层都是AVL树实现的,那么本文带你深入解析AVL和红黑树
注意:本篇博客在代码部分,强烈建议大家自己按照描述画出简图,否则容易晕
目录
1.AVL树
2.红黑树
1.AVL树
AVL是两位苏联数学家发明的,名字取于两个人的名字首字母
他们发明的动机是搜索二叉树有很明显的缺陷,一旦退化成单边,那么搜索的效率及其低下,所以他们想到可以用平衡的思想在搜索二叉树上做出改进
解决办法是:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不超过1(需要对树中的结点进行调整),即可降低树的高度,从而减少平均搜索长度
AVL树的特点是
- 左右子树都是AVL树
- 左右子树高度差绝对值不超过1(-1/0/1)
如果AVL树有n个节点,那么他的高度可以稳定保持在logn,搜索时间复杂度也是logn
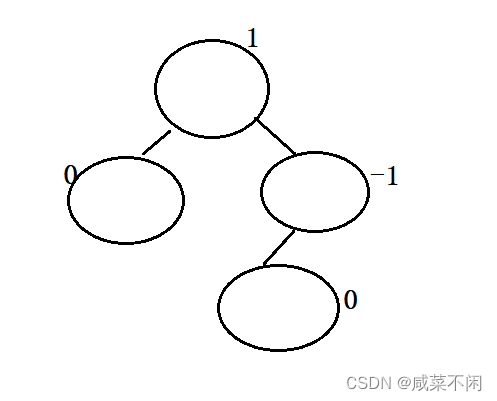
- AVL树节点的定义
这棵树需要左右孩子,并且为了以后调整(调整成平衡树),还需要保存它的父节点(根的父亲是nullptr),还有这个节点的值,以及平衡因子
平衡因子:该节点右树高度-左树高度 平衡因子可以是负数
之前规定过AVL树的左右高度差的绝对值不可以超过1,所以正常一颗平衡树的每个节点的平衡因子=0/1/-1
template
struct AVLNode
{
pair(K, V)& _kv;
AVLNode * left;
AVLNode * right;
AVLNode * parent;
int bf; //平衡因子
AVLNode(const pair(K,V)& kv)
:_kv(kv)
,left(nullptr)
,right(nullptr)
,parent(nullptr)
,bf(0)
{}
}; - AVL树的插入
bool insert(const pair& kv)
{
if (!_root)
{
_root = new Node(kv);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->left;
}
else
return false;
}
//现在走到了该插入的位置(cur)
cur = new Node(kv);
if (parent->_kv.first < kv.first)
{
parent->right = cur;
cur->parent = parent;
}
else
{
parent->left = cur;
cur->parent = parent;
}
//现在插入结束,但是不一定符合平衡树,现在要根据插入的位置调整二叉树各个节点的平衡因子
while (parent)
{
if (parent->right == cur)
parent->bf++;
else if (parent->left == cur)
parent->bf--;
if (parent->bf == 0)
return true; //说明插入之后两侧高度正好相等,很好不许要调整
else if (abs(parent->bf )== 1 )
{
//说明插入之前的parent->_kv==0,说明以双亲为根的二叉树的高度增加了一层,因此需要继续向上调整
cur = parent;
parent = parent->parent;
}
else if (parent->bf == 2 || parent->bf == -2)
{
//旋转
if (parent->bf == 2 && cur->bf == 1) //说明插在较高右子树的右侧
{
RotateL(parent); //右右=左单旋
}
else if (parent->bf == -2 && cur->bf == -1) //插在较高左子树的左侧
{
RotateR(parent); //左左=右单旋
}
else if (parent->bf == -2 && cur->bf == 1) //插在较高左子树的右侧
{
RotateLR(parent); //左右=左右旋
}
else if (parent->bf == 2 && cur->bf == -1) //插在较高右子树的左侧
{
RotateRL(parent); //右左=右左旋
}
else
{
assert(false);
}
break;
}
else
{
assert(false);
}
}
return true;
} 我们来说一下旋转的逻辑
首先看反正他就是四种插入的情况,因为parent的bf=2/-2,cur的bf=1/-1
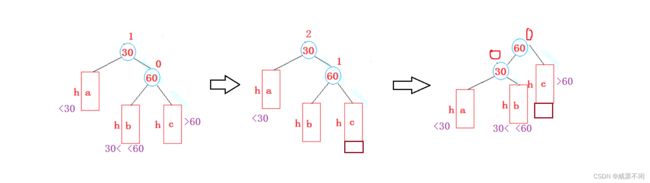
- parent的bf=2,cur的bf=1——左单旋
为什么叫左单旋?
单旋:只进行一个方向的旋转
左: 把不平衡的根换成了他孩子(插入了新节点的孩子)的左,并且把孩子的左给了他
方框代表子树(并不是一个节点)
是不是不感觉很合理,因为这种两个bf同正负是最好处理的情况
直接根据每颗子树的key区间,然后想办法旋转成最完美的平衡即可
那么怎么来写代码表示这个过程?
void RotateL(Node* parent)
{
Node* subR = parent->right; //首先定义出节点,代表右子树
Node* subRL = subR->left; //右子树的左孩子
parent->right = subRL;
if (!subRL) //如果右子树的左边是空,那么直接把父节点插入到空的地方
subR->left = parent;
Node* pparent = parent->parent; //祖父节点
subR->left = parent;//左树不是空
parent->parent = subR; //把原来的父节点的父改成subR
if (!pparent) //如果祖父节点是空
{
_root = subR; //subR变成根
subR->parent = pparent;
}
else //看subR到底应该是祖父节点的哪个孩子
{
if (pparent->left == parent)
parent->left = subR;
else
parent->right = subR;
subR->parent = pparent;
}
parent->bf = subR->bf = 0; //根据画图,我们知道最后两个的bf都是0
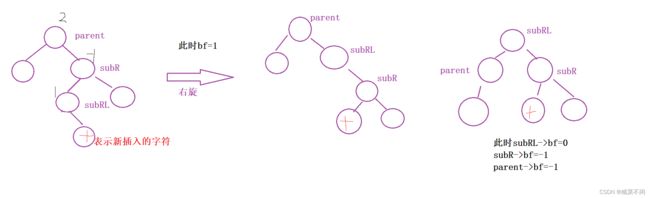
}- parent的bf=-2,cur的bf=-1——右单旋
为什么叫右单旋?
右:把不平衡的根换到他的孩子(插入了新节点的孩子)的右,并且把孩子的右给他
void RotateR(Node* parent)
{
Node* subL = parent->left;
Node* subLR = subL->right;
parent->left = subLR;
if (!subLR)
subL->right = parent;
Node* pparent = parent->parent;
subL->right = parent;
parent->parent = subL;
if (!pparent)
{
_root = subL;
_root->parent = nullptr;
}
else
{
if (pparent->left == parent)
pparent->left = subL;
else
pparent->right = subL;
subL->parent = pparent;
}
parent->bf = subL->bf = 0;
}- parent的bf=-2,cur的bf=1——左右单旋
简图
分三种情况,+节点插在左/右, subLR的另一个孩子没有,还有不就是+无论左右,另一个孩子都有
void RotateLR(Node* parent)
{
Node* subL= parent->right;
Node* subLR = subL->right;
int bf = subLR->bf;
RotateL(subL);
RotateR(parent);
if (1 == bf)
{
parent->bf = 0;
subL->bf = -1;
subLR->bf = 0;
}
else if (-1 == bf)
{
subLR->bf = 0;
subL->bf = 0;
parent->bf = 1;
}
else if (bf == 0)
{
subL->bf = 0;
subLR->bf = 0;
parent->bf = 0;
}
else
assert(false);
}- parent的bf=2,cur的bf=-1——右左单旋
按照这个看代码
void RotateRL(Node* parent)
{
Node* subR = parent->right;
Node* subRL = subR->left;
int bf = subRL->bf;
RotateR(subR);
RotateL(parent);
if (bf == 1)
{
subR->bf = 0;
subRL->bf = 0;
parent->bf = -1;
}
else if (bf == -1)
{
subRL->bf = 0;
subR->bf = 1;
parent->bf = 0;
}
else if (bf == 0)
{
subR->bf = 0;
subRL->bf = 0;
parent->bf = 0;
}
else
assert(false);
}
- 中序遍历
void Inorder()
{
_Inorder(_root);
}
void _Inorder(Node* root)
{
if (!root)
return;
_Inorder(root->left);
cout << root->_kv.first << ":" << root->_kv.second << endl;
_Inorder(root->right);
}- 树的高度
int Height(Node* root)
{
if (root == nullptr)
return 0;
int lh = Height(root->left);
int rh = Height(root->right);
return lh > rh ? lh + 1 : rh + 1; //返回左右子树中较大的+1(加上根)
}
- 判断一个树是不是平衡树
bool IsBalance()
{
return IsBalance(_root);
}
bool IsBalance(Node* root)
{
if (root == nullptr)
{
return true;
}
int leftHeight = Height(root->left);
int rightHeight = Height(root->right);
if (rightHeight - leftHeight != root->bf)
{
cout << root->_kv.first << "平衡因子异常" << endl;
return false;
}
return abs(rightHeight - leftHeight) < 2
&& IsBalance(root->left)
&& IsBalance(root->right);
}AVL树的删除很复杂,这里不再细讲
最后来看看AVL树的性能怎么样:如果需要一种查询高效且有序的数据结构,而且数
据的个数为静态的(即不会改变),可以考虑AVL树,但一个结构经常修改,就不太适合
2.红黑树
红黑树的底层还是平衡二叉搜索树,可以理解成和AVL是平起平坐的结构
顾名思义,他是有颜色的树(红黑),我们规定:
root节点一定是黑
不可以出现两个相邻的红色节点——根节点是红色,那么孩子一定是黑色
每个结点,从该结点到其所有后代直至NULL的简单路径上,均包含相同数目的黑色结点
每个NULL节点都是黑色的
满足上面的所有性质之后,就可以实现最长路径不超过最短路径的二倍 :
最长情况就是红黑交替,最短的情况就是全黑,为了满足黑色节点个数相等,那么在最长路径的黑色节点=最短路径的黑色节点,又最长路径红=黑,所以 最长路径的黑+红 = 2*最短路径的黑
所以红黑树的节点定义如下
enum Color {
red,
black
};
template
struct RBTreeNode
{
pair _kv;
RBTreeNode* _left;
RBTreeNode* _right;
RBTreeNode* _parent;
Color _col;
RBTreeNode(const pair& kv)
:_kv(kv)
, _left(nullptr)
, _right(nullptr)
, _parent(nullptr)
, _col(red)
{}
}; 下面我们来看看红黑树的一些功能
- 插入
肯定和AVL的插入在前半部分是一样的,思路都差不多
为什么一定要把新节点的颜色给成红色?
假设你给成黑色,确实,父节点不管是什么颜色都可以插入这个黑色的节点,但我们要保证最长路径不超过最短路径的2倍,也就是不可能一条路上好多黑色,一旦这样做,去把一长串的黑改成红,你觉得容易吗?
那给成红色,这时候如果父亲是红色,那么需要做出调整(马上讲),但是如果父亲是黑色,那么直接插入,爽歪歪
颜色调整
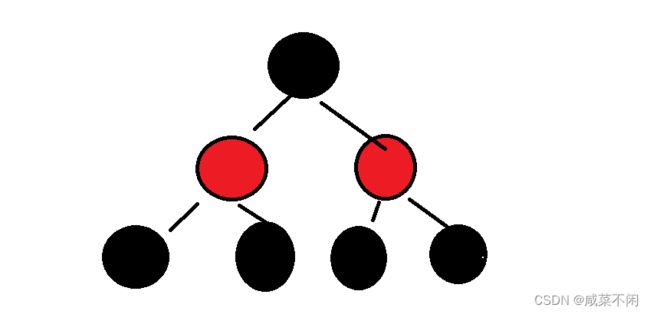
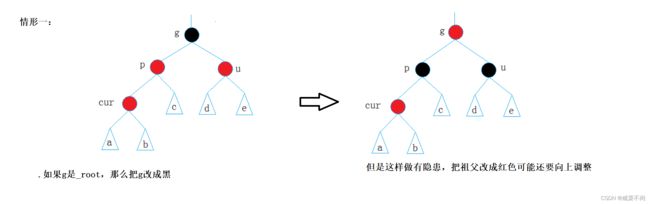
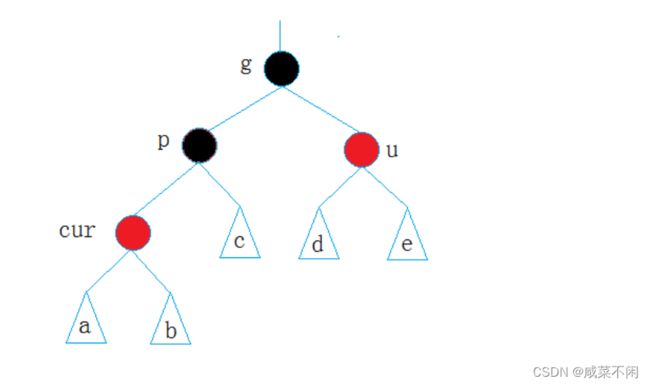
第一种情况: 叔叔节点存在且为红
注意:这里千万不能想当然认为,两个红色挨在一起,直接把父亲变红!
第二种情况:叔叔不存在/存在且为黑并且p是祖父的什么孩子,cur就是p的什么孩子
比如p是祖父的左孩子,cur就是祖父的左孩子
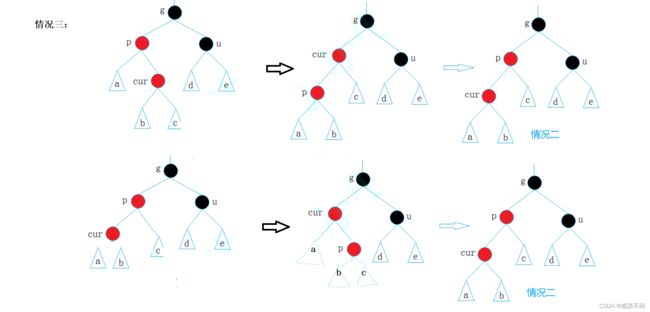
 第三种情况:把情况二变成折线 (也就是p是祖父的什么孩子,cur就是p的另一个方向的孩子,比如p是祖父的左孩子,cur就是p的右孩子)
第三种情况:把情况二变成折线 (也就是p是祖父的什么孩子,cur就是p的另一个方向的孩子,比如p是祖父的左孩子,cur就是p的右孩子)
折线的来源就是加上一句话紫色的部分(自己画一画就知道为什么这样是折线)
再次建议:自己把每一种情况画一个简图,然后对照着情况看我的代码!!!!!
bool Insert(const pair& kv)
{
if (_root == nullptr)
{
_root = new Node(kv);
_root->_col = black;
return true;
}
Node* parent = nullptr;
Node* cur = _root;
while (cur)
{
if (cur->_kv.first < kv.first)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_kv.first > kv.first)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
cur = new Node(kv);
cur->_col = red;
if (parent->_kv.first < kv.first)
{
parent->_right = cur;
cur->_parent = parent;
}
else
{
parent->_left = cur;
cur->_parent = parent;
}
while (parent && parent->_col == red) // 如果父亲是黑色,直接插入就没问题,所以要对父亲是红色的情况处理
{
Node* grandfater = parent->_parent;//记录祖父
if (parent == grandfater->_left) //如果他是祖父的左孩子
{
Node* uncle = grandfater->_right; //那么叔叔就是祖父的右孩子
// 情况一 uncle存在且为红
if (uncle && uncle->_col == red)
{
parent->_col = uncle->_col = black; //父亲和叔叔一起变黑
grandfater->_col = red; //祖父变红
cur = grandfater; //此时相当于要对祖父调整(向上调整),把cur(要调整的节点)赋值成祖父
parent = cur->_parent; //父亲节点相应改变
}
else //叔叔不存在/叔叔是黑(情况二/三),此时p已经是祖父的左孩子(大前提的if)
{
if (cur == parent->_left) //cur是左孩子 ,此时是情形二
{
RotateR(grandfater); //对祖父右旋
parent->_col = black; //此时的p是子树的根,设为黑
grandfater->_col = red;//祖父变成p的孩子,和cur一样设置成红色
}
else //cur是右孩子
{
// 情况三,也就是构成折线
RotateL(parent); //cur是p的右孩子,左旋p,然后变成情况二的cur是p左孩子
RotateR(grandfater); //在情况二且cur是p左孩子时,需要右旋祖父
cur->_col = black; //操作和情形二&&cur是左孩子的一样
grandfater->_col = red;
}
break; //这可子树已经没问题,但是此时应该向上调整
}
}
else //p是祖父的右孩子,和上面基本上没区别
{
Node* uncle = grandfater->_left; //那么叔叔就是祖父的左孩子
// 情况一 uncle存在且为红
if (uncle && uncle->_col == red)
{
parent->_col = uncle->_col = black; //父亲和叔叔一起变黑
grandfater->_col = red; //祖父变红
cur = grandfater; //此时相当于要对祖父调整(向上调整),把cur(要调整的节点)赋值成祖父
parent = cur->_parent; //父亲节点相应改变
}
else //叔叔不存在/叔叔是黑(情况二/三),此时p已经是祖父的右孩子(大前提的if)
{
if (cur == parent->_right) //cur是右孩子 ,此时是情形二
{
RotateL(grandfater); //对祖父左旋
parent->_col = black; //此时的p是子树的根,设为黑
grandfater->_col = red;//祖父变成p的孩子,和cur一样设置成红色
}
else //cur是左孩子
{
// 情况三,也就是构成折线
RotateR(parent); //cur是p的左孩子,右旋p,然后变成情况二的cur是p右孩子
RotateL(grandfater); //在情况二且cur是p右孩子时,需要左旋祖父
cur->_col = black; //操作和情形二&&cur是右孩子的一样
grandfater->_col = red;
}
break; //这可子树已经没问题,但是此时应该向上调整
}
}
}
_root->_col = black; //把根节点设为黑色
return true;
}
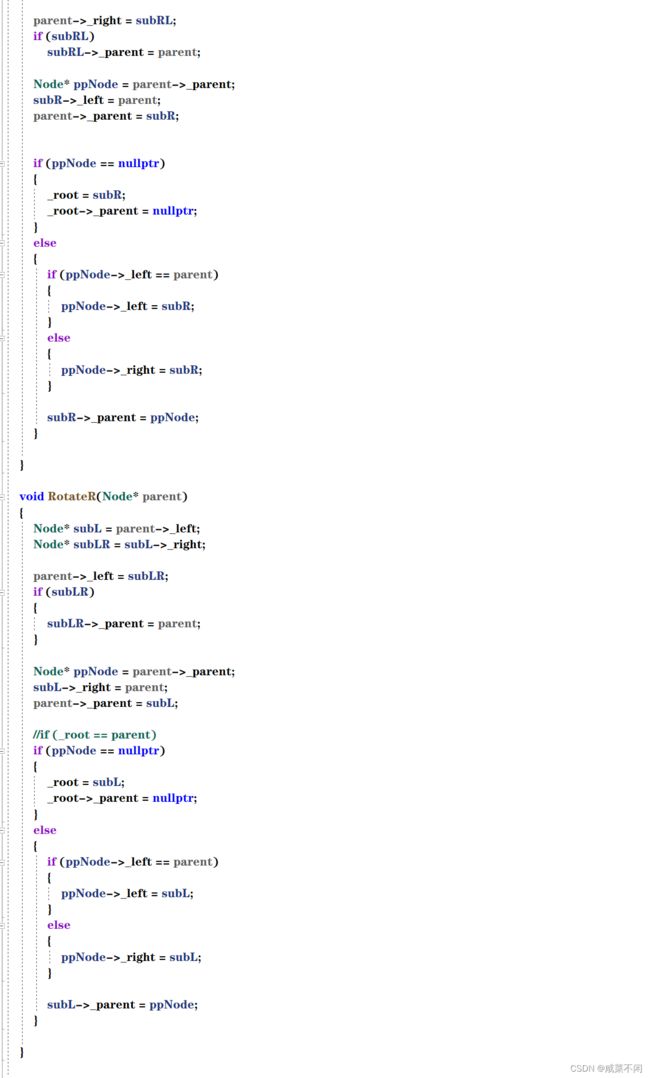
//下面实现旋转,其实和AVL没区别,只是没有bf因子
void RotateL(Node* parent)
{
Node* subR = parent->_right;
Node* subRL = subR->_left;
parent->_right = subRL;
if (subRL)
subRL->_parent = parent;
Node* ppNode = parent->_parent;
subR->_left = parent;
parent->_parent = subR;
if (ppNode == nullptr)
{
_root = subR;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subR;
}
else
{
ppNode->_right = subR;
}
subR->_parent = ppNode;
}
}
void RotateR(Node* parent)
{
Node* subL = parent->_left;
Node* subLR = subL->_right;
parent->_left = subLR;
if (subLR)
{
subLR->_parent = parent;
}
Node* ppNode = parent->_parent;
subL->_right = parent;
parent->_parent = subL;
//if (_root == parent)
if (ppNode == nullptr)
{
_root = subL;
_root->_parent = nullptr;
}
else
{
if (ppNode->_left == parent)
{
ppNode->_left = subL;
}
else
{
ppNode->_right = subL;
}
subL->_parent = ppNode;
}
} 至此红黑树最重要的部分已经完成,但是红黑树不止这一个操作!!!!
下一篇博客我们一起把map,set,红黑放在一起,讨论红黑的封装~