A*算法项目实践之三:优化A*的方法——不只是双向A*
A*算法项目实践之三:优化A*的方法——不只是双向A*
- 优化A*算法的必要性
- 优化方法1:使用hash和堆减少每个栅格的计算量
- 优化方法2:改进启发函数
- 优化方法3:实现双向A*
- Astar实现代码
在上文—— A*算法项目实践之二:基于障碍物避碰的栅格路径生成,我们得到了目标栅格路径,但发现每次计算路径所耗费的时间非常多,因此需要对A*搜索进行优化以提高其搜索速度,本文就笔者实际项目的一些经验来谈谈相关的方法,若有不对,请在评论区提醒笔者予以斧正 。
本项目基于VS2017,整个项目的代码以及上传到码云: A算法项目实践(正在更新中~)
参考文章:
1、A星算法原理及实现:
参考: https://blog.csdn.net/A_L_A_N/article/details/81392212
2、A星算法优化方法:
参考:
https://www.jianshu.com/p/b4ccd5b88487
https://zhuanlan.zhihu.com/p/80707067
https://www.cnblogs.com/xuuold/p/10366834.html
https://github.com/linyicheng1/motionPlan
优化A*算法的必要性
(1)A*拓展节点时,需要根据当前栅格搜索周围的8个栅格,距离终点越远、障碍物越多,所需要搜索的栅格就越多,且对每个栅格都需要花费一定的计算时间;
(2)A*算法的时间复杂度为O(n^ 2),n为问题的规模,例如本项目的n为91*360(可搜寻区域,栅格地图二维数组的行和列之积),最坏的情况时,本例的计算规模为(91*360)^2,因此计算量比较大。
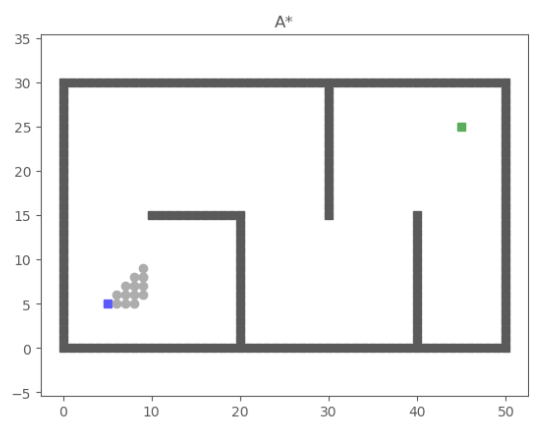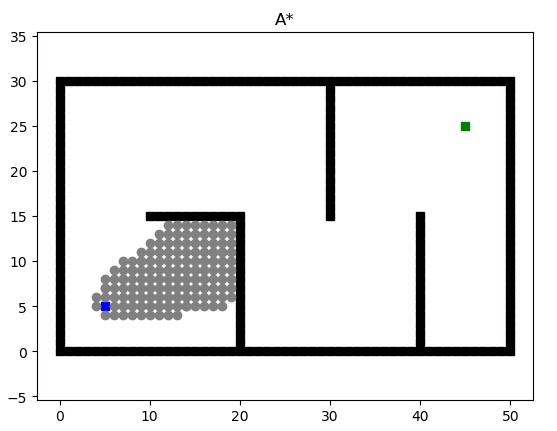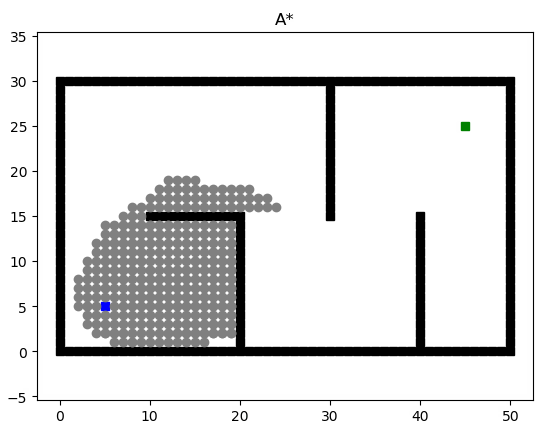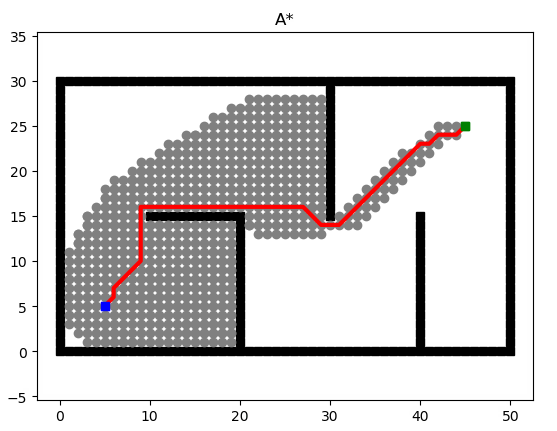
举例来说,若没有任何优化,则下图搜索出路径所耗费的时间为111.687s(这个时间与笔者电脑性能有关)
这个时间太大以至于无法满足项目要求,因此需要对A*搜索进行优化。
优化方法1:使用hash和堆减少每个栅格的计算量
回顾A*算法的流程,可以知道每个栅格的关键计算在与:
(1)从open和close表中的查找操作;
(2)从open表中搜索F最小栅格的操作。
理论上,(1)可以使用中的hash表查找(查找的效率为O(1)),(2)可以使用的堆搜索(搜索的效率为O(1))。
具体来说,(1)需要使用hash表备份open、close表,在c++中即使用unordered_set来同时备份open、close表,并将所有的查找操作都替换为unordered_set的查找。
(2)需要使用最小堆(以栅格的F值排序)来备份open表,在c++中即使用priority_queue来备份opene表,则F最小栅格即为堆顶栅格,但是这种方法并不适用,因为A*算法有一个这样的步骤:
if (它已经在开启列表中)
{
if (用 G 值为参考检查新的路径是否更好, 更低的G值意味着更好的路径)
{
把这一格的父节点改成当前格, 并且重新计算这一格的 GF 值.
}
}
算法会调整open表栅格的F值,从而对priority_queue造成破坏,因此本项目代码并没有使用priority_queue来优化(2)。
优化方法2:改进启发函数
启发函数的表达式为:
f(p) = g(p) + w(p) * h(p)
p表示某一栅格,g( p) 表示从起点 A移动到当前栅格p的移动耗费 (可沿斜方向移动);
h( p)表示从指定的方格移动到终点 的预计耗费 (h( p) 有很多计算方法, 比如欧几里得距离)
w( p) 为h( p)的系数。
可以参考该文章理解启发函数:A* 算法及优化思路
改进启发函数实际是动态加权方法的应用,即实现w( p) 函数———其原则为在搜索开始时,快速到达目的地所在区域更重要;在搜索结束时,得到到达目标的最佳路径更重要。
也就是说,当h( p)较大时,w( p)也应该较大,此时A*算法会尽快向终点扩展,搜索速度很快但会错过最优路径;当h( p)较小时,w( p)也应该较小,此时A*算法会倾向于搜索最优路径而减慢搜索速度。
这是典型的以性能换速度(笔者自编)——搜索路径的速度越快但搜索出的路径却越差(以长度、转弯数做指标),下面通过2个实验可以清晰看到这一点。
例子1:w( p)为1不变,此时算法搜索出的路径的是最优路径,耗费时间:71.58 s
例子2:w( p)为1、3(h( p)较小时,w( p)为1;h( p)较大时,w( p)为3),此时路径劣于最优路径,耗费时间:0.64 s
由此可见,在放弃搜索最优路径的情况下,使用动态加权可以大大缩短A*搜索的时间。
本文的动态加权实现代码为:
注:代码中的w( p)类似一个分段函数,读者在自己项目中的动态加权需要多次测试来得到这个分段函数。
int Astar::calcF(Point *point)
{
//动态加权
/*在搜索开始时,快速到达目的地所在区域更重要;
在搜索结束时,得到到达目标的最佳路径更重要。*/
//取当前栅格到终点栅格的距离
int w = static_cast<int>(sqrt(point->H));
//分情况取w值
if (w > 70)
w = 5;
else if (w > 50)
w = 4;
else if (w > 30)
w = 3;
else if (w > 10)
w = 2;
else
w = 1;
return point->G + w*point->H;
}
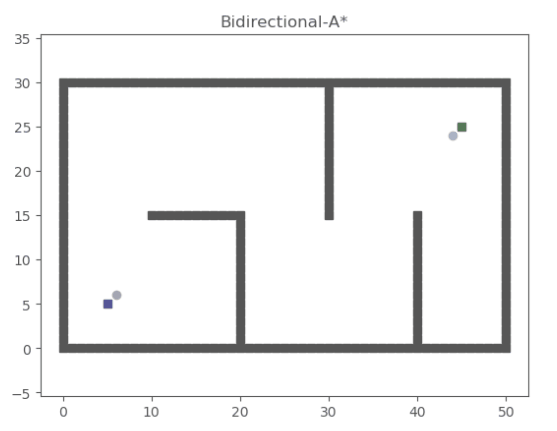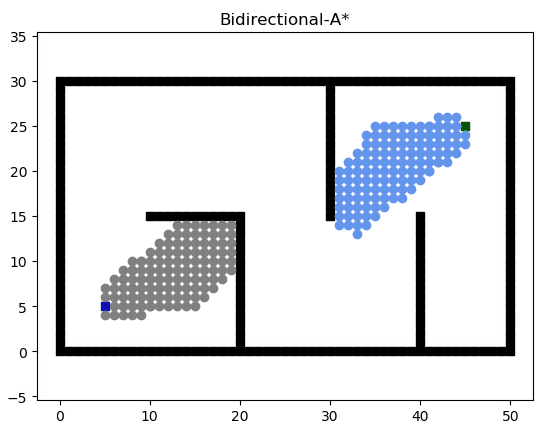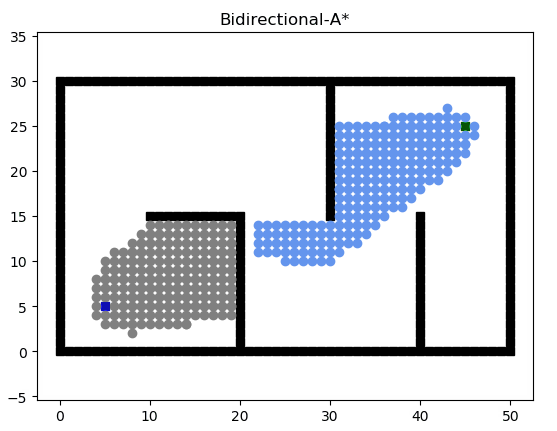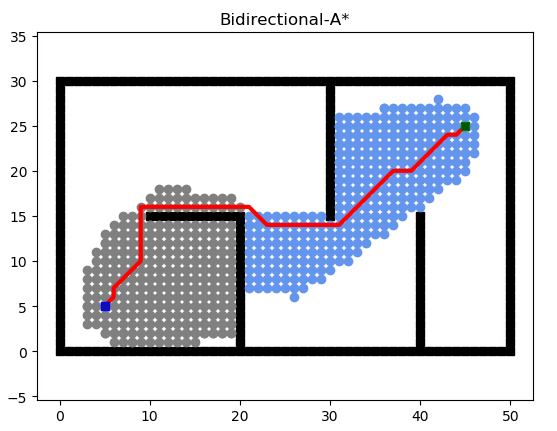
优化方法3:实现双向A*
双向A*搜索原理图:
双向A*搜索算法简要过程:
使用两个A*搜索,称为Astar1和Astar2
(1)Astar1从起点出发,Astar2从终点出发
(2)Astar1以Astar2的open表中的F值最小的栅格为终点进行扩展;
(3)Astar2以Astar1的open表中的F值最小的栅格为终点进行扩展;
(4)若Astar1或Astar2的open表为空,表示找不到,退出;
(5)重复(2)(3)(4) ,直到两个A*搜索都到达终点,此时两者相遇,表示成功找到路径,退出;
双向A*搜索算法详细过程:
把起始格添加到 "正向开启列表" ,把终点添加到 "反向开启列表"
将起点设置为正向开启列表的F值最低的格子cur_grid1,将终点设置为反向开启列表的F最低的格子cur_grid2
do
{
//正向A*
以将cur_grid1设为当前格.
把它切换到正向关闭列表.
对当前格相邻的8格中的每一个
if (它不可通过 || 已经在 "正向关闭列表" 中)
{
什么也不做.
}
if (它不在正向开启列表中)
{
把它添加进 "正向开启列表", 把当前格作为这一格的父节点, 并根据cur_grid2,计算这一格的 FGH
}
if (它已经在正向开启列表中)
{
if (用 G 值为参考检查新的路径是否更好, 更低的G值意味着更好的路径)
{
把这一格的父节点改成当前格, 并且重新计算这一格的 GF 值.
}
}
. if(cur_grid2已经在 "正向开启列表" ) 找到路径; break;
将cur_grid1重置为正向开启列表的F值最小的栅格
//反向A*
. 以将cur_grid2设为当前格.
把它切换到反向关闭列表.
对当前格相邻的8格中的每一个
if (它不可通过 || 已经在 "反向关闭列表" 中)
{
什么也不做.
}
if (它不在反向开启列表中)
{
把它添加进 "反向开启列表", 把当前格作为这一格的父节点, 并根据cur_grid1,计算这一格的 FGH
}
if (它已经在反向开启列表中)
{
if (用 G 值为参考检查新的路径是否更好, 更低的G值意味着更好的路径)
{
把这一格的父节点改成当前格, 并且重新计算这一格的 G F 值.
}
}
. if(cur_grid1已经在 "反向开启列表" ) 找到路径; break;
将cur_grid2重置为反向开启列表的F值最小的栅格
} while( 正向开启列表不为空 && 反向开启列表不为空)
如果正向开启列表或反向开启列表已经空了, 说明路径不存在.
最后从cur_grid1沿父节点回溯到起点,从cur_grid2沿父节点回溯到终点,合并两条路径得到最终路径.
具体实现代码:
//0、初始化两个当前点cur_grid1,cur_grid2
Point *cur_grid1 = openList.front();
Point *cur_grid2 = reverse_openList.front();
while (!openList.empty() && !reverse_openList.empty())
{
//正向A*
//正向1、
Point *curPoint = cur_grid1; //将cur_grid1设为当前格.
openList.remove(curPoint); //从正向开启列表中删除
//正向列表辅助结构删除栅格
openListOfHash.erase(*curPoint);
closeList.push_back(curPoint); //放到正向关闭列表
//正向关闭列表辅助结构增加栅格
closeListOfHash.insert(*curPoint);
//正向2、找到正向情况下当前周围八个格中可以通过的格子
std::vector<Point *> surroundPoints = getSurroundPoints(curPoint, isIgnoreCorner,true);
for (auto &target : surroundPoints)
{
//正向3、对某一个格子,如果它不在正向开启列表中,把它添加进 "正向开启列表", 把当前格作为这一格的父节点, 并根据cur_grid2,计算这一格的 FGH
if (!isInOpenList_Forward(target))
{
target->parent = curPoint;
target->G = calcG(curPoint, target);
target->H = calcH(target, cur_grid2);
target->F = calcF(target);
openList.push_back(target);
//正向开启列表辅助结构添加栅格
openListOfHash.insert(*target);
}
//正向4、对某一个格子,它在正向开启列表中,计算G值, 如果比原来的大, 就什么都不做, 否则设置它的父节点为当前点,并更新G和F
else
{
int tempG = calcG(curPoint, target);
if (tempG < target->G)
{
target->parent = curPoint;
target->G = tempG;
target->F = calcF(target);
}
}
}
//正向5、if(cur_grid2已经在 "正向开启列表" ) 找到路径; return;
if (isInOpenList_Forward(cur_grid2))
{
//Point *resPoint = GetPointOfList(openList, cur_grid2);
//从正向开启列表中找到cur_grid2所对应的grid1,使得从grid1回溯即可得到正向A*部分的路径
//直接从cur_grid2回溯,可得到反向A*部分的路径
auto gtePoint = GetPointOfList(openList, cur_grid2);
if (gtePoint != nullptr)
cur_grid1 = gtePoint;
//返回cur_grid1和cur_grid2
return make_pair(cur_grid1,cur_grid2);
}
//正向6、将cur_grid1重置为正向开启列表的F值最小的栅格
cur_grid1 = getLeastFpoint_Forward();
//反向A*
//反向1、
curPoint = cur_grid2; //将cur_grid2设为当前格.
reverse_openList.remove(curPoint); //从反向开启列表中删除
//反向列表辅助结构删除栅格
reverse_openListOfHash.erase(*curPoint);
reverse_closeList.push_back(curPoint); //放到正向关闭列表
//反向关闭列表辅助结构增加栅格
reverse_closeListOfHash.insert(*curPoint);
//反向2、找到反向情况下当前周围八个格中可以通过的格子
surroundPoints.clear();
surroundPoints = getSurroundPoints(curPoint, isIgnoreCorner, false);
for (auto &target : surroundPoints)
{
//反向3、对某一个格子,如果它不在反向开启列表中,把它添加进 "反向开启列表", 把当前格作为这一格的父节点, 并根据cur_grid1,计算这一格的 FGH
if (!isInOpenList_Reverse(target))
{
target->parent = curPoint;
target->G = calcG(curPoint, target);
target->H = calcH(target, cur_grid1);
target->F = calcF(target);
reverse_openList.push_back(target);
//反向开启列表辅助结构添加栅格
reverse_openListOfHash.insert(*target);
}
//反向4、对某一个格子,它在反向开启列表中,计算G值, 如果比原来的大, 就什么都不做, 否则设置它的父节点为当前点,并更新G和F
else
{
int tempG = calcG(curPoint, target);
if (tempG < target->G)
{
target->parent = curPoint;
target->G = tempG;
target->F = calcF(target);
}
}
}
// 反向5、if(cur_grid1已经在 "反向开启列表" ) 找到路径; return;
if (isInOpenList_Reverse(cur_grid1))
{
//从反向开启列表中找到cur_grid1所对应的grid2,使得从grid2回溯即可得到反向A*部分的路径
//直接从cur_grid1回溯,可得到正向A*部分的路径
auto gtePoint = GetPointOfList(reverse_openList, cur_grid1);
if (gtePoint != nullptr)
cur_grid2 = gtePoint;
//返回cur_grid1和cur_grid2
return make_pair(cur_grid1, cur_grid2);
}
//反向6、将cur_grid2重置为反向开启列表的F值最小的栅格
cur_grid2 = getLeastFpoint_Reverse();
}
Astar实现代码
项目的Astar.h文件代码:
//A*算法类
class Astar
{
public:
//删除类的默认构造函数、复制构造和赋值运算符
Astar() = delete;
Astar(const Astar&) = delete;
Astar& operator=(const Astar&) = delete;
//使用外部栅格地图maze构造
Astar(std::vector<std::vector<int>> &_maze);
//使用外部障碍物信息构造
Astar(int rows, int cols, const std::vector<car_info>& obstacle_info);
//使用默认析构函数
~Astar() = default;
//设置中心栅格距离车四个边界的格子字数
void SetCarInfo(int head, int heel, int left, int right);
//设置碰撞安全距离
void SetCollisionRadius(int len);
std::list<Point> GetPath(Point &startPoint, Point &endPoint, bool isIgnoreCorner);
void printGraphToCSV() const;
void printPathToGraphInCSV(const list<Point>& path);
private:
std::pair<Point *, Point *> findPath(Point &startPoint, Point &endPoint, bool isIgnoreCorner);
std::vector<Point *> getSurroundPoints(const Point *point, bool isIgnoreCorner, bool direction) const;
bool isCanreach(const Point *point, const Point *target, bool isIgnoreCorner,bool direction) const; //判断某点是否可以用于下一步判断,direction判别正向或反向A*
Point *GetPointOfList(const std::list<Point *> &list, const Point *point) const; //从开启/关闭列表中获取某点
Point *getLeastFpoint_Forward() const; //从正向开启列表中返回F值最小的节点
Point *getLeastFpoint_Reverse() const; //从反向开启列表中返回F值最小的节点
bool isInOpenList_Forward(const Point *point) const; //快速判断正向开启/关闭列表中是否包含某点
bool isInCloseList_Forward(const Point point) const; //快速判断正向开启/关闭列表中是否包含某点
bool isInOpenList_Reverse(const Point *point) const; //快速判断反向开启/关闭列表中是否包含某点
bool isInCloseList_Reverse(const Point point) const; //快速判断反向开启/关闭列表中是否包含某点
//计算FGH值
int calcG(Point *temp_start, Point *point);
int calcH(Point *point, Point *end);
int calcF(Point *point);
//栅格地图
std::vector<std::vector<int>> maze;
std::list<Point *> openList; //正向开启列表
std::list<Point *> closeList; //正向关闭列表
std::list<Point *> reverse_openList; //反向开启列表
std::list<Point *> reverse_closeList; //反向关闭列表
//辅助在开启列表和关闭列表中的搜索、查 找操作引入的结构
//用于搜索正向、反向开启列表和关闭列表中的栅格
std::unordered_set<Point, hash_fun_Point> openListOfHash,closeListOfHash;
std::unordered_set<Point, hash_fun_Point> reverse_openListOfHash, reverse_closeListOfHash;
bool CollisionCheck(int x, int y,int direction) const;
enum {
kCost1 = 10,//直移一格消耗10
kCost2 = 14, //斜移一格消耗14
};
//中心栅格距离载具前、尾、左和右边界的距离
int head_distance = 23, heel_distance = 24, left_distace = 8, right_distance = 8;
int CollisionRadius = 2;//碰撞安全距离,默认为2个栅格
};
本博文完,感谢您的阅读,望您不吝点赞之手,再次感谢。
欢迎继续阅读下一博文:A*算法项目实践之四:将栅格路径转换为直角坐标下的路径