吴恩达多分类逻辑回归与神经网络总结
吴恩达多分类逻辑回归与神经网络
文章目录
- 吴恩达多分类逻辑回归与神经网络
- 前言
- 一、多分类逻辑回归与神经网络
-
- 1、多分类逻辑回归
- 2、神经网络
- 二、程序代码
-
- 1. 多分类逻辑回归
-
- 1.1 读取数据集
- 1.2 数据预处理
- 1.3 数据可视化
- 1.4 定义sigmoid函数
- 1.5 定义代价函数
- 1.6 定义梯度下降函数
- 1.7 定义OVR分类器
- 1.8 定义预测分类器
- 1.9 检验正确率
- 2. 神经网络
-
- 2.1 读取数据集
- 2.2 定义前向神经网络
- 2.3 检验正确率
- 总结
前言
习题1:用逻辑回归来识别手写数字(0~9),我们将扩展我们在前面的逻辑回归的实现,并将其应用于一对一的分类。我们拥有其MATLAB本机格式的数据集。
习题2: 通过前向神经网络,实现数字预测。我们给定权重
一、多分类逻辑回归与神经网络
1、多分类逻辑回归
实现手写数字(0到9)的识别,需要扩展之前的逻辑回归,并将其应用于一对多的分类,其本质是将其划分为多个二分类问题。
我们先将(0~9)共10类,其每一类都是一个二分类的逻辑回归,我们设置其对应的参数:
0 ⟶ θ 0 1 ⟶ θ 1 2 ⟶ θ 2 3 ⟶ θ 3 4 ⟶ θ 4 5 ⟶ θ 5 6 ⟶ θ 6 7 ⟶ θ 7 8 ⟶ θ 8 9 ⟶ θ 9 \\\begin{array}{l} 0 \longrightarrow {\theta _0}\\ 1 \longrightarrow {\theta _1}\\ 2 \longrightarrow {\theta _2}\\ 3 \longrightarrow {\theta _3}\\ 4 \longrightarrow {\theta _4}\\ 5 \longrightarrow {\theta _5}\\ 6 \longrightarrow {\theta _6}\\ 7 \longrightarrow {\theta _7}\\ 8\longrightarrow {\theta _8}\\ 9 \longrightarrow {\theta _9} \end{array}\, 0⟶θ01⟶θ12⟶θ23⟶θ34⟶θ45⟶θ56⟶θ67⟶θ78⟶θ89⟶θ9
其中
θ i ∈ R n \\{\theta _{\rm{i}}} \in {R^{\rm{n}}} θi∈Rn
当训练 θ 0 {\theta _0} θ0时:
正样本:全为0的为正:记为1
负样本:else为负:记为0
同理可得: θ 1 {\theta _1} θ1、 θ 2 {\theta _2} θ2、 θ 3 {\theta _3} θ3、 θ 4 {\theta _4} θ4、 θ 5 {\theta _5} θ5、 θ 6 {\theta _6} θ6、 θ 7 {\theta _7} θ7、 θ 8 {\theta _8} θ8、 θ 9 {\theta _9} θ9
P ( y = 1 ∣ x ) = 1 1 + e − x θ T = h θ ( x ) \\P({\rm{y}} = 1{\rm{|x}}) = \frac{1}{{1 + {e^{ - x{\theta ^T}}}}}={h_\theta }(x)\\ P(y=1∣x)=1+e−xθT1=hθ(x)
给定一个图片X,把X分别放到训练器 θ 0 {\theta _0} θ0、 θ 1 {\theta _1} θ1、 θ 2 {\theta _2} θ2、 θ 3 {\theta _3} θ3、 θ 4 {\theta _4} θ4、 θ 5 {\theta _5} θ5、 θ 6 {\theta _6} θ6、 θ 7 {\theta _7} θ7、 θ 8 {\theta _8} θ8、 θ 9 {\theta _9} θ9中,得到不同的 h θ ( x ) {h_\theta }(x) hθ(x)即得到不同的概率值:
X → { h θ 0 ( x ) → P 0 h θ 1 ( x ) → P 1 ⋮ → ⋮ h θ 9 ( x ) → P 9 \\X \to \left\{ \begin{array}{l} {h_{\theta 0}}(x) \to {P_0}\\ {h_{\theta 1}}(x) \to {P_1}\\ \vdots \to \vdots \\ {h_{\theta 9}}(x) \to {P_9} \end{array} \right.\, X→⎩⎪⎪⎪⎨⎪⎪⎪⎧hθ0(x)→P0hθ1(x)→P1⋮→⋮hθ9(x)→P9
P = max ( P 0 , P 1 , P 2 , P 3 , P 4 , P 5 , P 6 , P 7 , P 8 , P 9 ) \\P = \max ({P_0},{P_1},{P_2},{P_3},{P_4},{P_5},{P_6},{P_7},{P_8},{P_9})\, P=max(P0,P1,P2,P3,P4,P5,P6,P7,P8,P9)
即( P 0 {P_0} P0~ P 9 {P_9} P9)中概率最大值所对应的 h θ ( x ) {h_\theta }(x) hθ(x)所对应的 θ {\theta } θ即为 X的表示的数字。
2、神经网络
该神经网络模型有三层:一个输入层,一个隐藏层,一个输出层。由于图片的尺寸是20×20,因此输出层单元就有401个(加上一个偏置单元)。神经网络的两个参数 θ 1 {\theta_1} θ1和 θ 2 {\theta_2} θ2已经给出,该网络在第二层有25个单元,输出层有10个单元(对应10个分类)。
二、程序代码
导入库:
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from scipy.io import loadmat
from scipy.optimize import minimize
1. 多分类逻辑回归
1.1 读取数据集
dress = 'E:\Python\python\吴恩达机器学习python作业代码\code\ex3-neural network\ex3data1.mat' # 这里面的像素是20*20的
data = loadmat(dress)
# print(data)
# c = type(data) # 查看data的数据类型(这里是字典)
#print(c)
#d = data.keys()
#print(d)
1.2 数据预处理
raw_X = data['X']
raw_Y = data['y']
# print(raw_X)
# print(raw_Y)
#查看数据维度
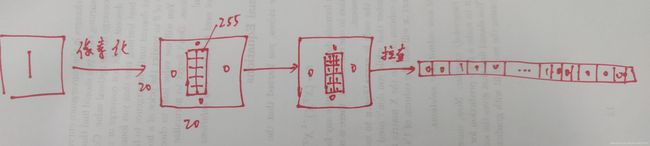
a = data['X'].shape # X的样本个数是5000个,特征是400维的,这里把20*20的图像拉直也就成了400个特征值
b = data['y'].shape # Y的样本个数是5000个,特征是1维的
# print(a)
# print(b)
1.3 数据可视化
pick_one = np.random.randint(0,5000) # 用numpy库里面的random模块下面的randint随机生成一个整数
image = raw_X[pick_one,:] # 把随机生成的这一个数当成一个索引,传到raw_X下面
fig,ax = plt.subplots(figsize=(1,1)) # 实例化:生成一个实例化图片
ax.imshow(image.reshape(20,20).T,cmap ='gray_r') # 传入图片,将数据维度400重新整理为(20,,20)的,转置可以改变图的方向
plt.xticks(np.array([]))
plt.yticks(np.array([]))
plt.show()
sample_idx = np.random.choice(np.arange(raw_X.shape[0]), 100)
sample_images = raw_X[sample_idx, :]
print(sample_images)
fig, ax_array = plt.subplots(nrows=10, ncols=10, sharey=True, sharex=True, figsize=(12, 12))
for r in range(10): # r表示行
for c in range(10): # c表示列
ax_array[r, c].matshow(np.array(sample_images[10 * r + c].reshape((20, 20))).T,cmap=matplotlib.cm.binary)
plt.xticks(np.array([]))
plt.yticks(np.array([]))
plt.show()
1.4 定义sigmoid函数
def sigmoid(z):
return 1 / (1 + np.exp(-z))
fig, ax = plt.subplots(figsize=(9,6)) # 设置图片尺寸
x1 = np.arange(-10, 10, 0.1)
ax.plot(x1, sigmoid(x1), c='r',label = 'g(z)') # 绘制g(z)的图像
ax.set_title("Sigmoid Function", fontsize=14) # 图名字,字号14
ax.set_xlabel("z", fontsize=10) # x轴标签,字号10
ax.set_ylabel("g(z)", fontsize=10) # y轴标签,字号10
ax.tick_params(axis = 'both', which = 'major', labelsize = 10)
ax.legend(loc='lower right')
plt.show()
1.5 定义代价函数
代价函数:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) log ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) log ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 \\J(\theta ) = - \frac{{\rm{1}}}{{\rm{m}}}\sum\limits_{i = 1}^m {[{y^{(i)}}\log ({h_\theta }({x^{(i)}}))} + (1 - {y^{(i)}})\log (1 - {h_\theta }({x^{(i)}}))]{\mkern 1mu} + \frac{\lambda }{{2m}}\sum\limits_{j = 1}^n {\theta _j^2} \, J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
θ = ( θ 0 ⋯ θ n − 1 ) \\\theta = \left( {{\theta _0} \cdots {\theta _{n - 1}}} \right)\, θ=(θ0⋯θn−1)
定义目标变量y:
y = ( y 1 ⋮ y m ) \\y = \left( \begin{array}{l} {y_1}\\ \vdots \\ {y_m} \end{array} \right)\, y=⎝⎜⎛y1⋮ym⎠⎟⎞

def CostFunction(theta, X, y, learningRate):
# input:参数值theta,特征:X,标签:y,正则化参数,学习率
# output:当前参数下的交叉熵损失
# tudo:根据特征和输入的数据计算交叉熵损失函数
# step1: 将theta、X、y转化成numpy的矩阵
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
# step2 根据公式计算损失函数(不包含正则化)
first = np.multiply(-y, np.log(sigmoid(X * theta.T)))
second = np.multiply((1 - y), np.log(1 - sigmoid(X * theta.T)))
# step3:根据公式计算公式中的正则化部分
reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[:,1:theta.shape[1]], 2)) # 这里从theta_1开始,而不是从theta_0开始
# reg = (learningRate / (2 * len(X))) * np.sum(np.power(theta[1:], 2))也可以
# step4 把上面3个式子结果加起来得到整体损失函数
SumCost = np.sum(first - second) / len(X) + reg
return SumCost
正则化从第二项开始的解释:
首先正则化主要是为了防止过拟合,而过拟合一般表现为模型对于输入的微小改变产生了输出的较大差异,这主要是由于有些参数 θ i {\theta_i} θi (i≠0)过大的关系,通过对 θ i {\theta_i} θi 进行惩罚,可以缓解这种问题。
而如果对 θ 0 {\theta_0} θ0进行惩罚,其实是没有作用的,因为在对输出结果的影响中,参数 θ 0 {\theta_0} θ0对于输入的改变是不敏感的,不管输入改变是大还是小,参数 θ 0 {\theta_0} θ0的影响就只是加个偏置而已。
举个例子,在线性回归的训练集中, θ 0 {\theta_0} θ0和 θ 1 {\theta_1} θ1都表现得很好,但是在测试集上发生了过拟合, θ 0 {\theta_0} θ0是不背这个锅的,因为它对于所有的数据都是一视同仁的(都只是给它们加个偏置),要背锅的是 θ 1 {\theta_1} θ1,因为它会对不同的数据产生不一样的加权。或者说,模型对于输入的微小改变产生了输出的较大差异,这是因为模型的“曲率”太大,而模型的曲率是由 θ 1 {\theta_1} θ1决定的, θ 0 {\theta_0} θ0不影响曲率(对输入进行求导, θ 0 {\theta_0} θ0是直接约掉的)。
1.6 定义梯度下降函数
def Gradient(theta, X, y, learningRate):
# input:参数值theta,特征:,标签:y,正则化参数
# output:当前参数下的梯度
# tudo:根据特征和输入的数据计算梯度
# step1:将theta、X、y转化成numpy的矩阵
theta = np.matrix(theta)
X = np.matrix(X)
y = np.matrix(y)
# step2:将theta矩阵拉直(转化成一个向量)
parameters = int(theta.ravel().shape[1])
grad = np.zeros(parameters)
# step3: 计算预测的误差
error = sigmoid(X * theta.T) - y
# step4: 计算梯度
for i in range(parameters):
term = np.multiply(error, X[:, i])
if (i == 0):
grad[i] = np.sum(term) / len(X)
else:
grad[i] = (np.sum(term) / len(X)) + ((learningRate / len(X)) * theta[:, i])
return grad
1.7 定义OVR分类器
def OVR(X, y, num_labels, learning_rate):
rows = X.shape[0] # rows为X的行数(5000)
params = X.shape[1] # params为X的列数即参数个数(400)
# k * (n + 1) array for the parameters of each of the k classifiers
all_theta = np.zeros((num_labels, params + 1)) # 这里的+1就是拓展的那一维(10,401)
# insert a column of ones at the beginning for the intercept term
X = np.insert(X, 0, values=np.ones(rows), axis=1) #在X的第0列插入一列1,方向axis=1竖着插 X(5000,401)
# labels are 1-indexed instead of 0-indexed
for i in range(1, num_labels + 1): # i从1到10
theta = np.zeros(params + 1) # 初始化一个401维的0向量
y_i = np.array([1 if label == i else 0 for label in y]) # 当label=i时,输出1,否则输出0
y_i = np.reshape(y_i, (rows, 1)) # 把y_i reshape成一个列向量
# minimize the objective function
fmin = minimize(fun=CostFunction, x0=theta, args=(X, y_i, learning_rate), method='TNC', jac=Gradient)
all_theta[i - 1, :] = fmin.x
return all_theta
查看分类器各个参数的维度:
# 查看分类器各个参数的维度,均为假设,函数中不需要体现
rows = data['X'].shape[0]
params = data['X'].shape[1]
all_theta = np.zeros((10, params + 1))
X = np.insert(data['X'], 0, values=np.ones(rows), axis=1)
theta = np.zeros(params + 1)
y_0 = np.array([1 if label == 0 else 0 for label in data['y']])
y_0 = np.reshape(y_0, (rows, 1))
k = np.unique(data['y']) #看下有几类标签
print(X.shape, y_0.shape, theta.shape, all_theta.shape,k)
all_theta = OVR(raw_X, raw_Y, 10, 1)
print('查看所有的theta',all_theta)
1.8 定义预测分类器
def predict_all(X, all_theta):
# input:参数值theta,测试数据X
# output:预测值
# todo:根据特征和输入的数据计算梯度
# step1 获取矩阵维度信息
rows = X.shape[0]
# params = X.shape[1]
# num_labels = all_theta.shape[0]
# step2 把矩阵X加入一行1的元素
X = np.insert(X, 0, values=np.ones(rows), axis=1)
# step3 把X和all_theta转化为numpy矩阵
X = np.matrix(X)
all_theta = np.matrix(all_theta)
# step4 计算样本属于每一类的概率
h = sigmoid(X * all_theta.T)
# step 找到每个样本中预测概率的最大值
h_argmax = np.argmax(h, axis=1)
# 因为我们的数组是0索引的,所以需要为真正的标签+1
h_argmax = h_argmax + 1
return h_argmax
1.9 检验正确率
y_pred = predict_all(data['X'], all_theta)
correct = [1 if a == b else 0 for (a,b) in zip(y_pred,data['y'])]
accuracy = (sum(map(int,correct))/float(len(correct)))
print('accuracy = {0}%'.format(accuracy*100))
accuracy = 94.46%
2. 神经网络
2.1 读取数据集
weight = loadmat("E:\Python\python\吴恩达机器学习python作业代码\code\ex3-neural network/ex3weights.mat")
theta1, theta2 = weight['Theta1'], weight['Theta2']
print(theta1.shape, theta2.shape)
(25, 401) (10, 26)
2.2 定义前向神经网络
def predict(theta1, theta2, X):
# input:参数值theta,测试数据X
# output:预测值
# todo:对输入参数进行前向传播
# step1 获取矩阵维度信息
m = X.shape[0] # m为X的行数
# params = X.shape[1]
# num_labels = all_theta.shape[0]
# step2 找到每个样本中概率最大的值
ones = np.ones([m, 1]) # 定义一个m行1列的numpy数组,值为1
X = np.column_stack([ones,X]) # 为X添加偏置项
z2 = np.dot(X, theta1.T)
a2 = sigmoid(z2)
a2 = np.column_stack([ones, a2]) # 为a2添加偏置项
a3 = sigmoid(np.dot(a2, theta2.T))
# step3 找到每个样本中概率最大的值
p = np.argmax(a3, axis=1) + 1
# 因为这里的数组是0索引的,所以我们需要为真正的标签+1
p = np.reshape(p, [m, 1])
return p
2.3 检验正确率
p = predict(theta1, theta2, raw_X)
# temp里面的值是True(=1)和False(=0)
temp = (p == raw_Y)
prob = np.mean(temp)
print('Training Set Accuracy = {0}%'.format(prob*100))
Training Set Accuracy = 97.52%
总结
predict()预测函数和一对多逻辑回归predict_all()略有不同。在神经网络模型中我们不需要h = Sigmoid(X * theta_all.T) 求出概率这一步,因为神经网络的输出结果不是优化好的参数,而是直接的结果,也就是概率。可以看出,神经网络模型的代码量更小,速度也更快。我们可以直观的对比一下:逻辑回归在计算时花费的时间远远大于多分类逻辑回归。