李宏毅《机器学习》|2021笔记：10. 神经网络改进流程

参考文章：
梯度下降：https://www.bilibili.com/video/BV1r64y1s7fU
早停法：https://www.datalearner.com/blog/1051537860479157
正则化：https://www.cnblogs.com/jianxinzhou/p/4083921.html
2017笔记：https://blog.csdn.net/oldmao_2001/article/details/90714657
2021笔记：https://zhuanlan.zhihu.com/p/395527363

2021.09.30
LeeML-Notes：P18，P19

2021.10.18 更新
LeeML2021:P5,P6,P8,P9内容：
① 2.4.1 Critical Point: small gradient
② 2.0 Batch 大小，对优化的影响
③ 2.4.2 Adaptive Learning Rate
④ 2.5 Batch Normalization(批次标准化）

祝大家国庆快乐，学个习为祖国庆生！
<--------感谢评论、答疑、指正！--------->

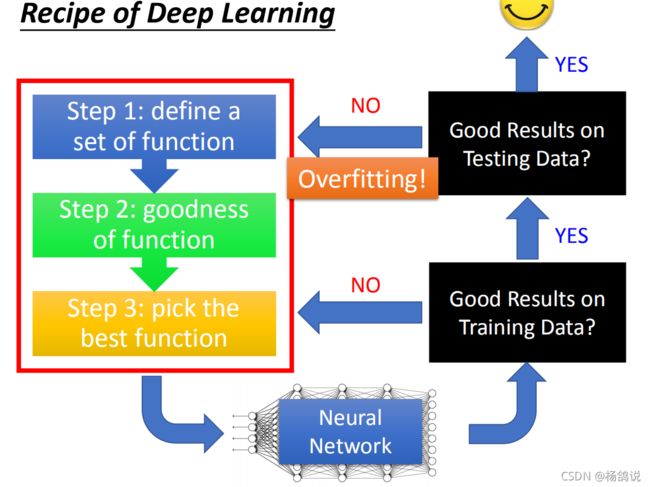
1. 修改流程

• ① 如果training set上的结果表现不好，那么就要去neural network在一些调整
• ② 如果training set上的结果表现很好，testing set表现不好，那么是过拟合
• ③ 如果在testing set表现的很好，就意味成功了。

2 是否过拟合？没有

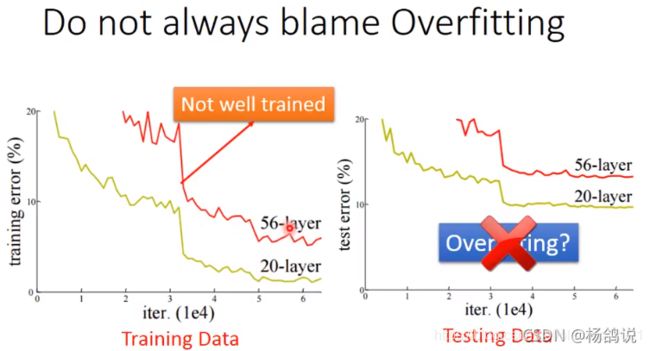
首先看有没有过拟合？也就是训练数据表现好，测试数据不行

上图中，56层的模型对比20层的模型，无论是在training set还是testing set上表现都要差，这个事情并不是Overfitting的原因，而是没有训练好

2.0 Batch 大小，对优化的影响

<----------------2021新增内容1--------------->

• 【基础知识】

• 将一笔大型资料分若干批次计算 loss 和梯度，从而更新参数
• 每看完一个epoch 就把这笔大型资料打乱，然后重新分批次
• 这样能保证每个 epoch 中的 batch 资料不同，避免偶然性

• 【大小批次的运算时间对比】

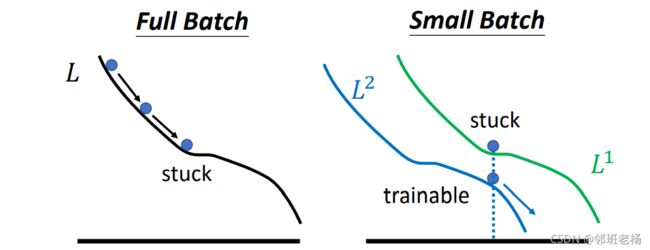
  • 大批次的单次运算时间长但效果好
  • 小批次的单次运算时间短但效果差，需要运算多次效果才好
  • GPU可平行运行，有平行运算时，单次更新大小批次耗时差不多，而 1 个 epoch中大批次耗时更短

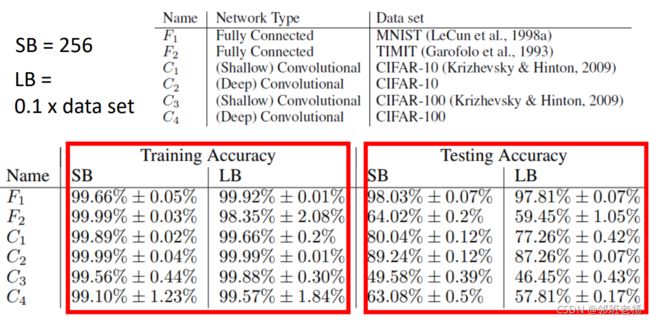
• 【大小批次的性能对比】

  • 小批次有更好的性能。由图可知同一个模型，同一个网络，training误差随着batch size 的增大而增大，testing 的误差也是

  • 小批次不容易被卡住

    

    • 例子是满批次，那么卡住就卡住了，
    • 如果换成小批次，因为不同的 batch 用不同的 loss function。换了个 loss 函数就更不容易卡住

  • 大批次面临的问题是overfitting

    

    • 红框框中可以看出在训练时 SB（小批次）和 LB（大批次）的准确率都高
    • 在testing 时，SB的准确率还是比较高，而LB的准确率则更差点，此时 LB面临的问题是overfitting。

• 【总结】

  小批次在 1 个 epoch 中的速度很慢，耗时很长，但是小批次在优化过程性能更好，在测试时的性能也更好。而批次大小是一个超参数，需要自行设定。

  

2.1 隐层神经元个数

model = Sequential()
model.add(Dense(input_dim=28*28,units=500,activation='sigmoid'))
model.add(Dense(units=500,activation='sigmoid'))
model.add(Dense(units=10,activation='softmax'))

units=500 改为 units=689 效果会好一点

model = Sequential()
model.add(Dense(input_dim=28*28,units=689,activation='sigmoid'))
model.add(Dense(units=689,activation='sigmoid'))
model.add(Dense(units=10,activation='softmax'))

2.2 增加深度

deep learning 就是很deep的样子，那么才三层，用for添加10层

model.add(Dense(input_dim=28*28,units=689,activation='sigmoid'))
model.add(Dense(units=689,activation='sigmoid'))
model.add(Dense(units=689,activation='sigmoid'))
for _ in range(10):
    model.add(Dense(units=689,activation='sigmoid'))
    
model.add(Dense(units=10,activation='softmax'))

• 训练效果并没有变好
• deep learning 并不是越deep越好
• 隐层Neure调整，对整体效果也不一定有助益

2.3 调整激活函数

2.3.1 ReLU

用sigmoid函数 ，高层会表现不好，改用ReLU

#搭NN:
model = Sequential()
model.add(Dense(input_dim=28*28,units=689,activation='relu'))
model.add(Dense(units=689,activation='relu'))
model.add(Dense(units=10,activation='softmax'))

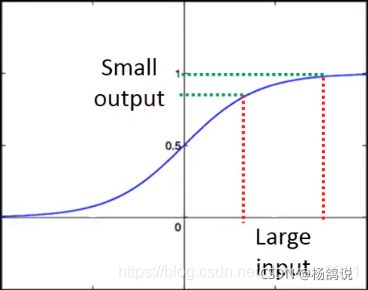
• 【sigmoid层多表现不好的原因】

因为越来越扁平 梯度越来越小 即使步伐很大，因为斜率很小，所以基本上没有什么收敛，这种现象叫做 梯度消失。

• 【ReLU表现好的原因】

① 比起sigmoid，计算速度快（看形状就知道啦）
② 看原作者论文提到，这个是有生物学上有一定原因
③ 相当于无限个不同bias的sigmoid函数叠加
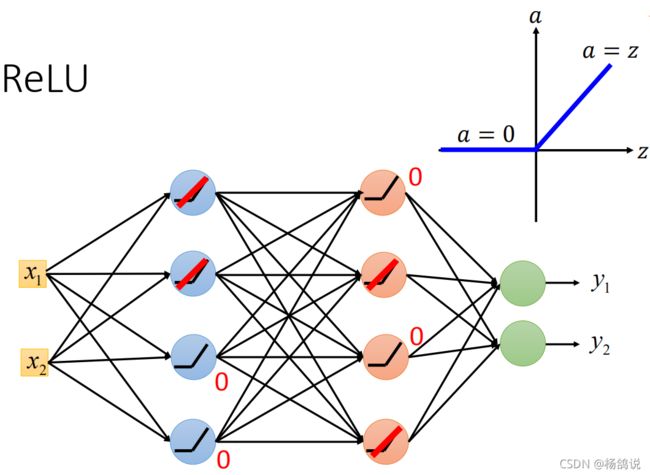
④ 解决了梯度消失问题（最重要），ReLU可以分成两部分，小于0的输出0，大于0的输出原值，也就是线性的，所以上面的神经网络可以看成：

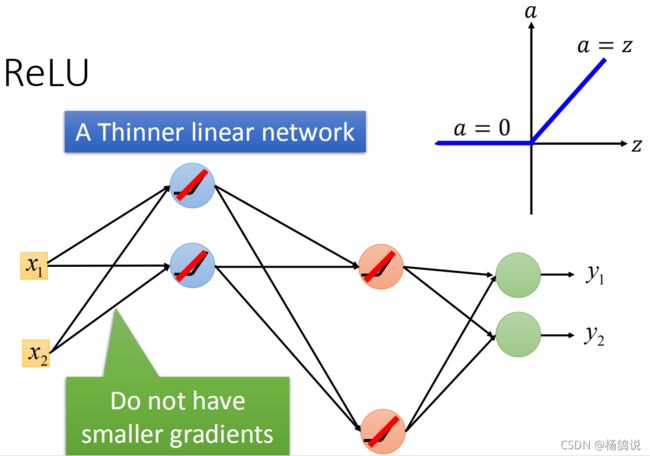
• 剩下的所有神经元都是线性的，所以整个网络变成一个瘦长的线性网络：A Thinner linear network，在这个线性神经元的网络中梯度在传递的过程中是不会递减的。
• 虽然单个神经元是线性的，但是整个神经网络是非线性的，原因是：很多个线性的神经元可以形成非线性的结果，例如用很小的方块可以拼成一个大圆是一个道理。

面试常问：ReLU是不可导的，如何进行反向传播（要计算偏导）？
忽略不可导的那个点(0点)。

• 【ReLU函数变种】
  

  • 【变种1 】leaky ReLU

    ReLU在input小于0时，output为0，这时微分为0，你就没有办法updata你的参数，所有我们就希望在input小于0时，output有一点的值(input小于0时，output等于0.01乘以input)，这被叫做leaky ReLU。

  • 【变种2】 Parametric ReLU

    Parametric ReLU在input小于0时，output等于$\alpha z$为neural的一个参数，可以通过training data学习出来，甚至每个neural都可以有不同的$\alpha$值。

  • 【变种3】 Exponential linear Unit (ELU)

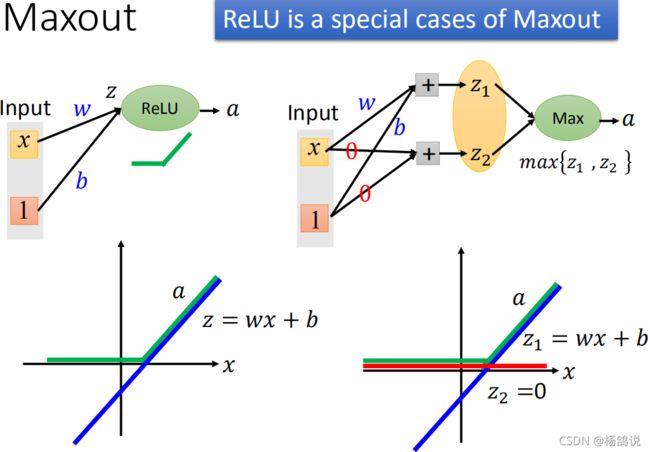
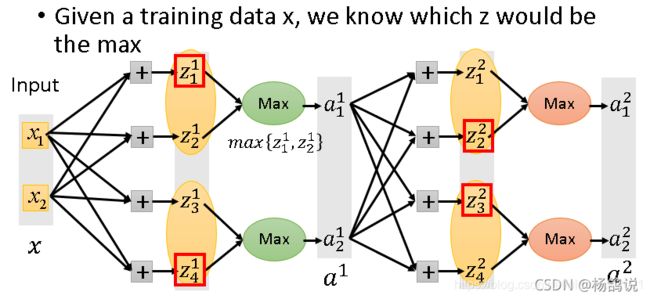
2.3.2 Maxout

• ① ReLU是特殊的Maxout

• ② Maxout可以是两线性函数结合，也可以3个

• ③ 简化过程

• 没有被training到的element，那么它连接的w就不会被training到了，在做BP时，只会training在图上颜色深的实线，不会training不是max value的weight。这表面上看是一个问题，但实际上不是一个问题。

• 当你给到不同的input时，得到的z的值是不同的，max value是不一样的，因为我们有很多training data，而neural structure不断的变化，实际上每一个weight都会被training。

2.4 调整梯度下降方式

2.4.1 Critical Point: small gradient

<----------------2021新增内容1--------------->

我们在优化模型中，会遇到 Critical Point（临界点） 中的局部最小值和鞍点。他们会使得梯度接近于0，导致损失值无法继续降低。

2.4.1.1 Shaddle point 鞍点

• 但其实，临界点中的saddle point(鞍点)还能找到办法让loss降低
• $\theta$的 loss 函数用在附近点${\theta }^{\prime }$的泰勒展开式近似表示如下：

• 下图中的纵坐标是 loss 值，横坐标是向量
• 一阶微分乘自变量差值是 y轴上的绿色长度（可以用tan来理解）
• 二阶微分乘两个自变量差值是 y轴上的红色长度。【疑问1：怎么得出来的？】

【当梯度接近0时】

当梯度接近0时，即，g=0时：

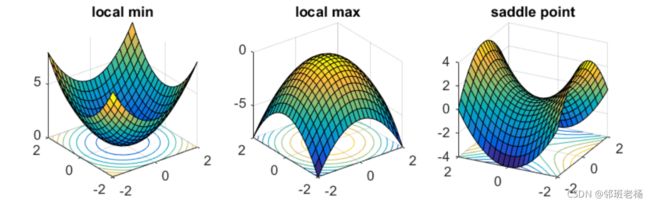
• 以${\theta }^{\prime }$为中心点，周围损失值都比它大的，那么${\theta }^{\prime }$为损失函数的局部最小点
• 以${\theta }^{\prime }$为中心点，周围损失值都比它小的，那么${\theta }^{\prime }$为损失函数的局部最大点
• 以${\theta }^{\prime }$为中心点，周围损失值有比大，有比它小，那么${\theta }^{\prime }$为损失函数的鞍点

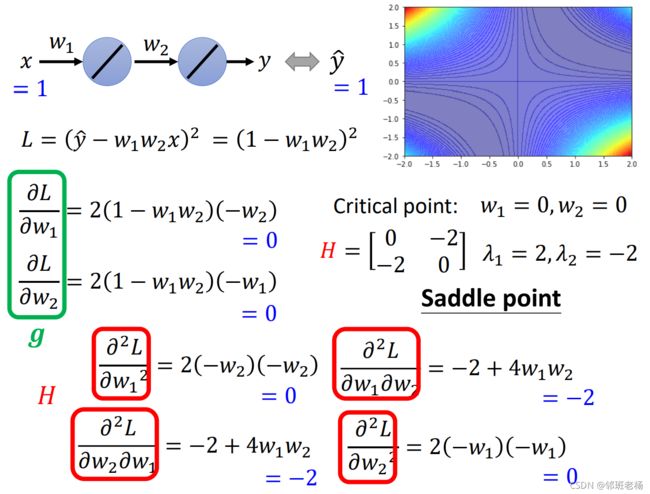
【举例计算】

• ① 求特征向量

• 我们通过让梯度g=0，得知Critical point: 1 = 0, 2 = 0
• 计算出来了H和两个特征值为2和-2，所以该点是个鞍点。

• ② 通过特征值和特征向量，确定梯度下降的方向
  鞍点处的 H矩阵中，特征值有正有负，这些正负能指导我们更新参数的方向

2.4.1.2 local minima

看似陷入了局部最低，但是高维上依旧能找到路进行下降，所以我们认为的局部低点是几乎不存在的，我们不需要考虑。

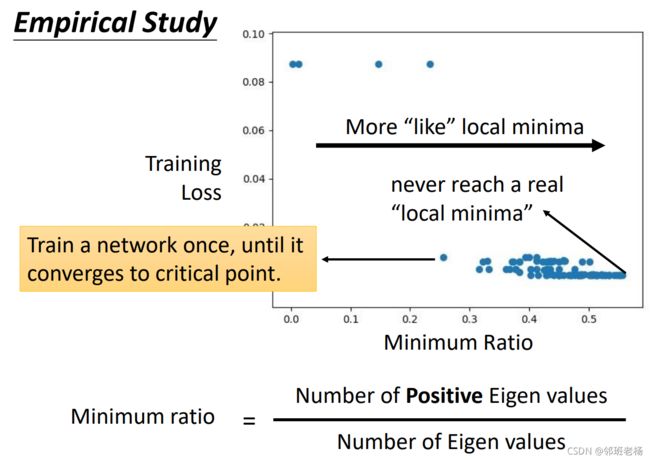
实验也可以证明：

训练一个网络，直到它卡在临界点。在实验中记录特征值中正值的比例（minimum ratio），当正值比例越大，该位置就更像局部最小值点，因为下降的路越少。我们发现实验的所有临界点都没有达到正值比例100%，最高竟然停留在50%附近，这证明有一半的特征值是负数，即还有一半的路 可以使loss降低，所以在实际问题中，local minima几乎不存在，也就不是梯度下降的一个痛点。

2.4.2 Adaptive Learning Rate（自适应学习率）

<----------------2021新增内容3--------------->

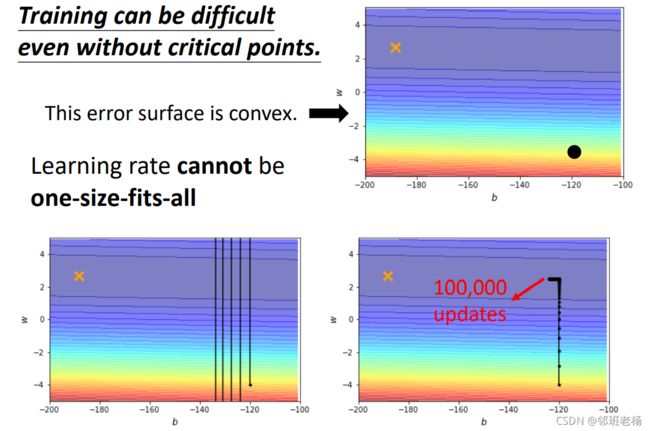
• loss无法继续下降有时候并非是梯度很小接近为0
• 上图所示，loss没有减小的时候，梯度并未为零（红圈）
• 这种情况往往是步伐太大，出现反复横跳的情况

• 出发点黑色圆点，目标点黄×
• 当学习率为$10^{-2}$时候，我们w在山谷两端反复横跳，始终无法达到目标点（黄×）
• 当学习率为$10^{-7}$时候，没有出现相互横调，走到山谷了，但是在梯度很小的地方收敛非常慢（步伐太小了），也无法达到目标点（黄×）

2.4.2.1 Root Mean Square

• 解决了梯度大的时候，步伐会小，防止了抖动；
• 梯度小的时候，步伐会大，防止因步伐太小无法达到终点

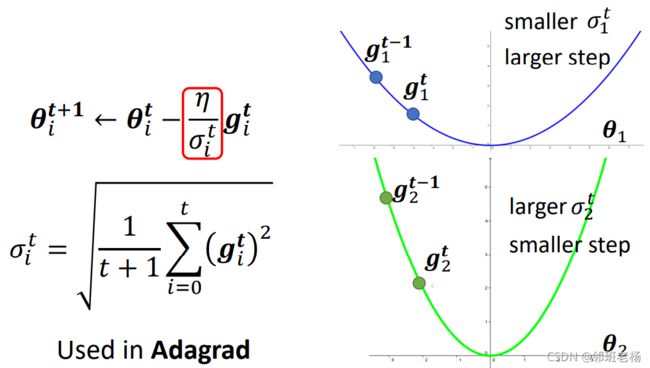
2.4.2.2 Adagrad

详见 《梯度下降》相应部分：https://blog.csdn.net/wistonty11/article/details/120118145

• 比Root Mean Square方法变化了一点，$\eta =\frac{\eta }{\sqrt{1+t}}$
• 思想是开始走快点，随着步数t，步伐越来越小

这样可以保证，

2.4.2.3 RMSprop

• .AdaGrad算法的改进。鉴于神经网络都是非凸条件下的，RMSProp在非凸条件下结果更好，

• 改变梯度累积为指数衰减的移动平均以丢弃遥远的过去历史。

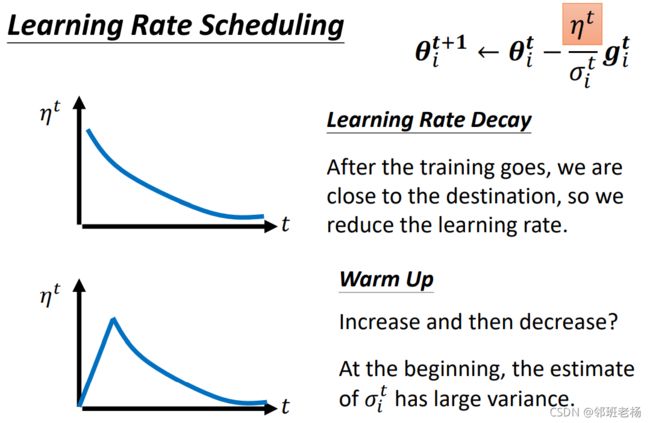
2.4.2.4 Learning Rate Scheduling

• 学习率先增大，后减小
• 思想是开始谨慎试探，慢慢增加
• 后面越到目的地，那么走起来越谨慎，步伐越小

2.4.3 Momentum

加上Momentum之后，每一次移动的方向是 negative gardient加上Momentum的方向, 类似一个惯性。

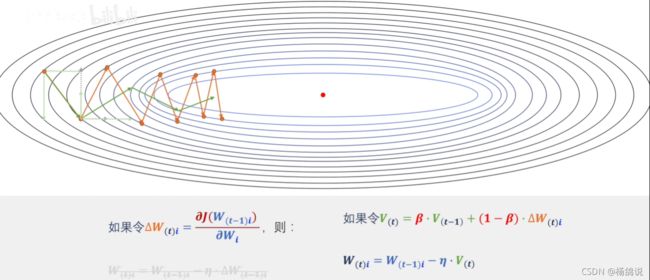
• ① 梯度下降方向是垂直等高线的，如果只是梯度方向，如图情况会是橘色线，会抖动

• ② Momentum（动量法）是为了对冲mini-batch带来的抖动。

• ③ 我们进行向量分解，发现竖直方向是抖动的，而水平方向是一致的

• ④ 那我们就用过去的向量+这步的梯度： $V_{(t)}=V_{(t-1)}+\Delta W_{(t)i}$

• ⑤ 但我们需要个权重，把非常早的向量忽略不计，就有了$V_{(t)}=\beta V_{(t-1)}+（1-\beta ）\Delta W_{(t)i}$

  

• ⑥ Momentum不能保证全局最优，但是有希望跳出局部最优

李宏毅老师给的简答一点，只是分别给了权重

2.4.4 Adam

• RMSprop修改步长。Momentum调整方向，都考虑到了历史数据和权重。

RMSProp + Momentum，这里就是要注意Adam的参数值一般来说就按推荐的取，不用调。

2.5 Batch Normalization(批次标准化）

我们有时候会遇到这种情况：

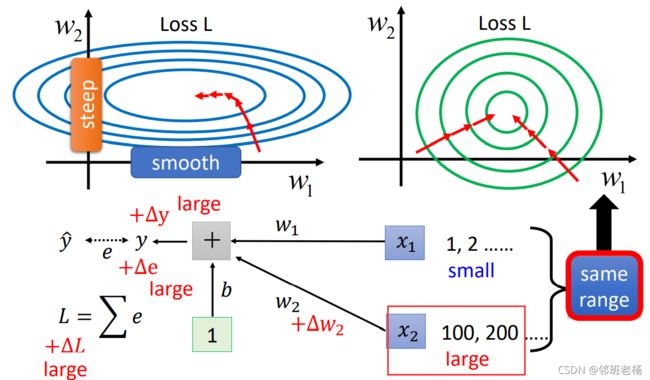
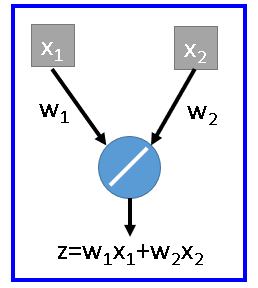
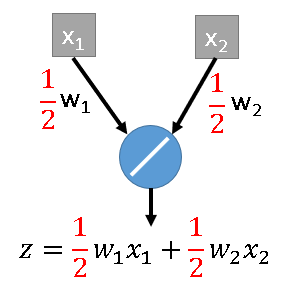
• x1数值很小，x2数值较大
• 意味着权重w2增加一点点，那么结果就会增加很多，如w1,w2的图，是个扁圆
• 扁圆在梯度下降的时候需要不时的变换方向，没有圆形下降速度快
• 我们想通过Feature Normalization，使得扁圆变圆

2.5.1 训练数据的特征标准版

【Feature Normalization的一个方法】

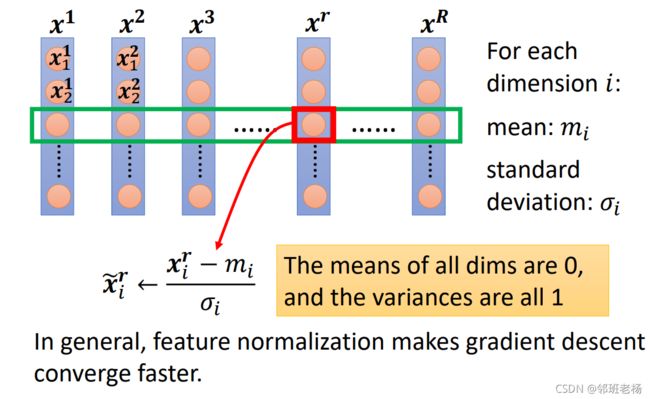
① 对数据进行标准化

• 这个batch中有R个数据，每个数据i维
• 对同一纬度进行归一化，使其所有$x_i$~的平均值均为0，方差均为1

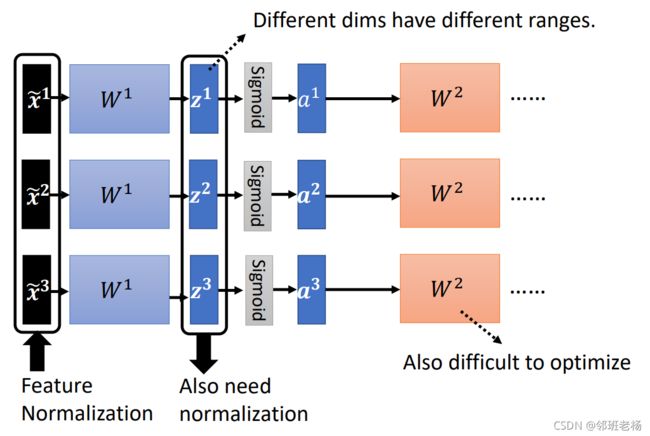
② 隐藏层 z 进行标准化

• 【原因】

经过feature normalization后的 x~ 都在同一量级，但是 W1 的不同维度可能有不同的量级，因此计算出来的 z 在不同维度也可能有不同的量级。所以隐藏层 z 也需要进行标准化。

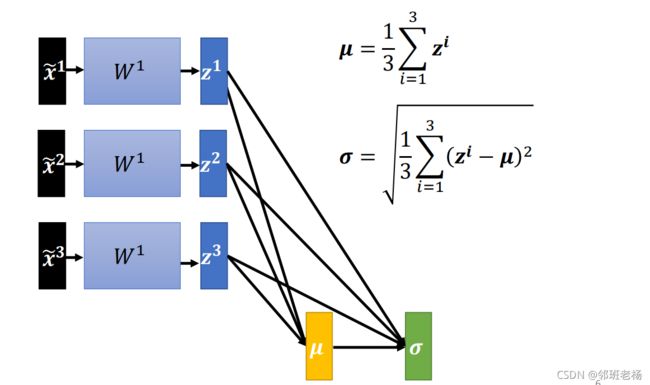
• 【隐藏层 z 标准化方法】

通过右边式子计算平均值和标准差，同个向量中的不同元素分别计算，不同向量同一维度的元素放在一起计算

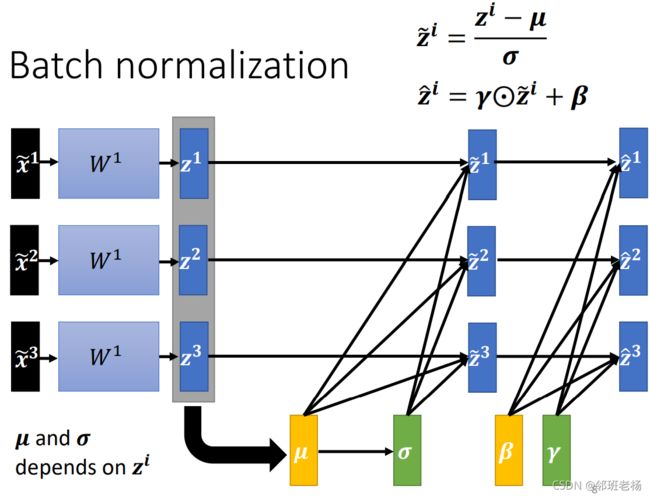
计算出来的平均值向量和标准差向量大小取决于 z，所以这是一个大型网络，假如将所有的资料输入进去，GPU的内存不够存所有的训练资料，所以分批次输入资料，保证一次只对一个batch 进行标准化。但是批次标准化适用于 batch size 大的，因为只要batch够大就能足以代表全部分布。

往往在批次标准化后还要加一层网络，用于调整 z 的分布，通常刚开始设 γ=1，β=0，等到后面再改变γ，β的大小来调整 z 的分布，这两个参数需要被learn出来。

2.5.2 测试集数据的特征标准版

在testing中没有batch，而training时有 t 个batch，就有 t 个 μ。所以通过计算training中的 moving average（滑动平均）来代替 testing的 μ和西伽马！

3 过拟合

训练集上表现很好，但测试集表现欠佳

常用的防止过拟合的方法是对模型加正则项，如L1、L2，dropout，但深度神经网络希望通过加深网络层次减少优化的参数，同时可以得到更好的优化结果，Early stopping的使用可以通过在模型训练整个过程中截取保存结果最优的参数模型，防止过拟合。

3.1 Early Stopping

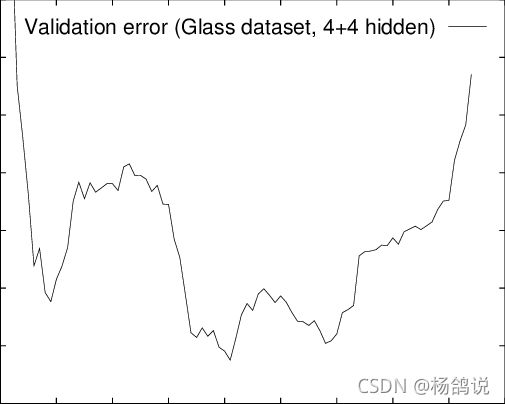
• 迭代次数增多后，达到一定程度后产生过拟合。从图中可以看出，训练集精度一直在提升，但是test set的损失值先下降后上升。若是在early stopping的位置保存模型，则不必反复训练模型，即可找到最优解。

• 其基本含义是在训练中计算模型在验证集上的表现，当模型在验证集上的表现开始下降的时候，停止训练，这样就能避免继续训练导致过拟合的问题。

【主要步骤】

• ① 将原始的训练数据集划分成训练集和验证集
• ② 只在训练集上进行训练，并每个一个周期计算模型在验证集上的误差，例如，每15次epoch（mini batch训练中的一个周期）
• ③ 当模型在验证集上的误差比上一次训练结果差的时候停止训练
• ④ 使用上一次迭代结果中的参数作为模型的最终参数

上图在训练集迭代到400次的时候出现了16个局部最低。也就是以可能出现短暂的最低点，然后继续继续变小。因此，我们需要一个停止的标准来实施早停法。使得它可以产生最低的泛化错误，同时也可以有最好的性价比，即给定泛化错误下的最小训练时间。停止标准有很多，也很灵活，大约有三种:

参考材料：https://www.datalearner.com/blog/1051537860479157

3.2 Regularization

【思路】

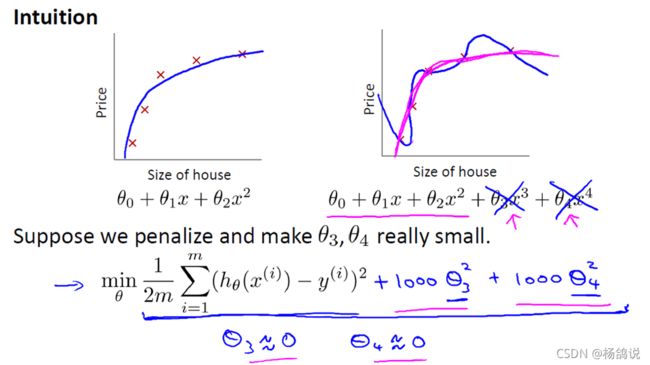
• 如果我们用一个更高次的多项式去拟合，它能很好地拟合训练集，但却并不是一个好的结果，因为它过度拟合了数据

• 让我们考虑下面的假设，我们想要加上惩罚项，从而使参数 θ3 和 θ4 足够的小。

• 1000 只是我随便写的某个较大的数字而已。现在，如果我们要最小化这个函数，那么为了最小化这个新的代价函数，我们要让 θ3 和 θ4 尽可能小

• 所以，当我们最小化这个新的代价函数时， 我们将使 θ3 的值接近于 0，同样 θ4 的值也接近于 0，就像我们忽略了这两个值一样。如果我们做到这一点（ θ3 和 θ4 接近 0 ），那么我们将得到一个近似的二次函数。

• 实际上，这些参数的值越小，通常对应于越光滑的函数，也就是更加简单的函数。因此 就不易发生过拟合的问题。

• 如果我们像惩罚 θ3 和 θ4 这样惩罚其它参数，就达到了更好地拟合训练数据，又很好的适应训练集

【L1 Regularization】

• sgn表示符号函数，如果w是正的，sgn(w)>0，如果w是负的，sgn(w)<0

• 每一次更新时参数时，我们一定要去减一个$\eta \lambda sgn(w^t)$值(w是正的，就是减去一个值；若w是负的，就是加上一个值，让参数变大)。

• L2、L1都可以让参数变小，但是有所不同的，若w是一个很大的值，L2下降的很快，很快就会变得很小，在接近0时，下降的很慢，会保留一些接近01的值；L1的话，减去一个固定的值(比较小的值)，所以下降的很慢。所以，通过L1-Norm training 出来的model，参数会有很大的值。

【L2 Regularization】

• 在update参数的时候，其实是在update之前就已近把参数乘以一个小于1的值(ηλ都是很小的值)，这样每次都会让weight小一点。最后会慢慢变小趋近于0，但是会与后一项梯度的值达到平衡，使得最后的值不等于0。L2的Regularization 又叫做Weight Decay，就像人脑将没有用的神经元去除。

两种方法基本上都是让图形更光滑，让特征值w 更快接近0。L2 Regularization是按比例衰减；而L1 Regularization是按固定值衰减

3.3 Dropout

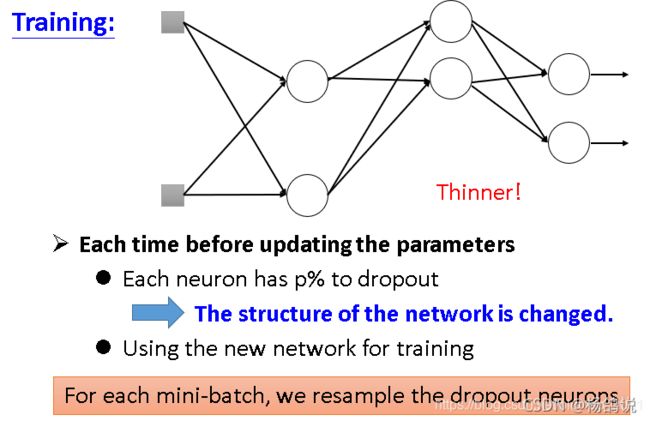
就是随机把一些支持机（神经元）去掉

• 只在训练集上进行抓爆(P%的概率扔掉)
• 在test上权重要乘以（1-p%）

【原理】

• 原始过程

• 做法

【严谨思路】

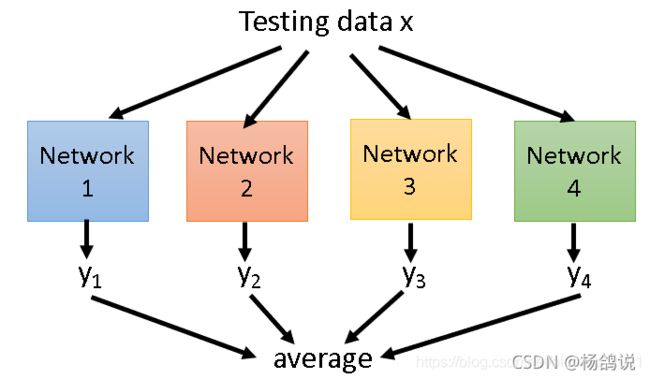
• 我们一批训练数据data x
• 应该把所有抓爆情况的模型都算一下 再求平均

【严谨思路问题】这样神经网络变化是指数级的 ，没法实现

【Dropout方法】

• 抓爆概率P%,那么 测试集上所有权中*（1-P%）
• 你会发现 两者很相似

【例子验证相似】

我没听清会不会别的例子也可以

那么可能经过抓爆后变成四种情况：

概率一算 一样